Индексы направлений

Возьмем направление на рис.8

Спроектирум фигуру в плоскость ХУ

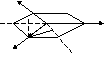U X Y U Z

Y

1 _{-1/2 -1/2} 0

X 2 -1 -1 0

Рис.9

Таблица 7

Направление [2110]

Общая запись: [u v i w], i= -(u+v)

При записи в фигурных и угловых скобках первые 3 индекса возможны с минусом, такая запись будет верна.

Лекция 5 Формулы геометрической кристаллографии.

Индексы – это лицо монокристалла.

I.Расстояние между плоскостями, входящими в одно семейство параллельных плоскостей (hkl):

d= a/h²+k²+l²

II.Определение угла между плоскостями (h₁k₁l₁) и (h₂k₂l₂):

h₁h₂+k₁k₂+l₁l₂

cos=

h₁+k₁+l₁h₂+k₂+l₂

III.Определение принадлежности направления плоскости:

(h k l) [UVW]

Если hU+kV+lW=0, то направление принадлежит плоскости.

Эта формула имеет практическое значение в эпитаксии. Это одно из условий протекания эпитаксии.

IV.Определение линии пересечения двух плоскостей: (h₁k₁l₁) и (h₂k₂l₂)

h₁k₁l₁h₁k₁l₁Крайные отбрасываются, а остальные

перекрестно перемножаются.

h₂k₂l₂h₂k₂l₂

Кристаллографические проекции.

В основе метода построения кристаллографических проекций лежит закон о постоянстве углов в кристалле.

I. Сферические координаты.

Определяются две координаты и.

Сферические проекции можно получить:

1.Если две грани путем параллельного переноса свести в одну точку –центр сферы проекции и продолжить до пересечения со сферой.

Сферическая проекция– это совокупность точек на сфере. Этот комплекс называетсяпланарным комплексом(все грани в одну точку).

2.Если к каждой грани построить

перпендикуляр и продлить его до

пересечения со сферй, то мы полу-

чим совокупность точек на сфере.

Совокупность называется поляр-

нымкомплексом.

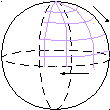NНа поверхность шара наносится вспо-

могательная сетка.

-долгота, один из меридианов нулевой

Долгота определяет угол между нуле-

вым меридианом и меридианом, опре-

деляющим пл-ть (по часовой стрелке).

O Вторая координата,-полярное рас-

стояние, называется расстояние, заклю-

ченное между полюсом и соответствую-

щей точкой; отсчитывается по меридиа-

S ну, проходящему через полюс и данную

точку.

Существует несколько сеток.

Сетка Вульфа:ее диаметр 20 см

цена деления 2⁰

Недостаток метода сферических проекций заключается в объемности.