Лекция 1

Кристаллография — наука, изучающая процессы образования, формы, структуру и физико-химические свойства кристаллов.

Классификация кристаллов

К

проводники

ристаллы

Кристаллы

Проводники могут быть только поликристаллами, тогда как полупроводники и диэлектрики — и монокристаллами, и поликристаллами.

Внутреннее строение кристаллов определяет их внешнюю форму.

Кристалл представляет собой твердое тело, имеющее в трех направлениях определенный порядок (период).

Исторические этапы развития кристаллографии.

Кристаллохимия — наука, изучающая зависимость внутреннего строения и физических свойств от химического состава.

1. 1669 год. Датский ученый Стено сформулировал закон постоянства гранных углов.

2. 1784 год. Гаюи сделал попытку объяснить этот закон правильностью внутреннего строения кристаллов, при этом он предполагал, что все частицы кристаллов имеют форму многогранников.

3. 1813 год. Волластен сделал предположение, что все частицы имеют шаровидную форму.

4. В 1835 году Франкенгейм, а в 1848 году Браве ввели понятие пространственной решетки.

5. Федоров, Шенфинс, Барлоу в 1885-1896 годах независимо друг от друга вывели 230 пространственных групп симметрии.

6. 1912 год. Лауэ изучением кристаллических структур с помощью рентгеновских лучей подтвердил, что пространственных групп симметрии действительно всего 230.

Для описания внешней формы кристалла строго математически выводятся 32 точечные группы.

Внешняя форма — проявление физических свойств кристаллов, а свойства кристаллов зависят от закономерного внутреннего строения.

Каждому кристаллическому материалу присущ свой «узор» или порядок, характеризующийся определенной симметрией по расположению частиц в пространстве. Вследствие закономерности и симметрии кристаллы однородны и анизотропны.

Кристаллы бывают дискретные (прерывные) и сплошные (однородные).

Дискретность проявляется в том, что свойства кристалла отличаются в местах, где есть частица, и где она отсутствует; либо в местах, где есть частицы двух сортов.

Сплошной считается среда тогда, когда размеры части кристалла, который рассматривается, меньше, чем весь поликристалл, но больше размера элементарных частиц.

Основные законы кристаллографии.

1. Закон плоскогранности и прямореберности.

Кристаллы ограняются плоскими поверхностями — гранями, они пересекаются по ребрам, а ребра сходятся в вершинах.

2. Закон внешней формы (постоянства углов) Стено-Ломоносова-Ромэ-Делиля.

Углы между соответственными гранями (и ребрами) во всех кристаллах одного и того же вещества постоянны (для данной полиморфной модификации)

2. Анизотропия свойств кристаллов

Анизотропия — различие свойств по разным направлениям.

Это основная характерная особенность кристаллических веществ.

Все кристаллы однородны, анизотропны, симметричны. Причина — их внутренняя атомная структура регулярна.

Расстояние между атомами и силы связи между ними в разных направлениях разные, поэтому возникает анизотропия физических свойств.

В параллельных направлениях свойства одинаковы.

Кристалл — это тело с правильным внутренним строением, физически и химически однородное, все векторные свойства которого одинаковы в параллельных и связанных симметрией направлениях.

Пространственная решетка

Для ее построения возьмем точку А₀ — исходный узел решетки (рис.1). Перенесем его на одно и то же расстояние а вправо несколько раз (а=А₀А₁). Получим ряд узлов А_0, А₁ и т.д.

Ряд — совокупность узлов, лежащих вдоль прямой и повторяющихся через равные промежутки. Это ряд пространственной решетки.

Расстояние а называется элементарной трансляцией или периодом тран

сляции, параметром ряда. Аналогично получается другой ряд с периодом

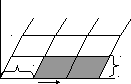трансляции в, отличным от а. От каж

дого узла проводим линии, параллель

В₂ ные рядам. При пересечении двух ря

С₁ В₁ дов получилась плоская сетка.

с а в Плоская сетка — совокупность уз

лов, расположенных в одной плоскос

А₀ А₁ А₂ А₃ ти и находящихся в вершинах системы

_рис.1 равных параллелограммов и смежных по целым сторонам (серая штриховка).

Третий ряд берем вне плоскости чертежа. Элементарная трансляцияс, отличная от а и в. Проведя линии, получим элементарный параллелепипед повторяемости, который построен на трех элементарных трансляциях а, в, с и называется элементарной ячейкой (рис.2).

С_n Z

С₁ В_n

с

B₁  

а  Y

А₀ А₁ А₂ А_n в

Рис.2 Рис.3

Х

Если провести установку элементарной ячейки (рис.3), то можно ввести 6 ее характеристик: 3 метрических а, в, с и 3 угла (против оси х), (против оси у), (против оси z).

За ребра ячейки принимают те направления в пространственной решетке, в которых величина трансляции наименьшая, которые наилучшим образом отражают симметрию решетки.