
- •Лекция 1
- •Лекция 2
- •Отражение
- •Вращение
- •Инверсия
- •Отражение-вращение
- •Вращение-инверсия
- •Взаимодействие элементов симметрии (теоремы сложения).
- •Теорема №1
- •Обратная теорема
- •Виды симметрии кристаллов.
- •Виды симметрии кристаллов, обладающих единичным направлением.
- •Виды симметрии кристаллов без единичных направлений.
- •Лекция 4 Характеристика сингоний.
- •Обозначение плоскостей и направлений в кубических кристаллах.
- •Порядок нахождения индексов плоскостей.
- •Аспекты эквивалентности плоскостей.
- •Индексы направлений.
- •Алгоритм определения индексов направлений.
- •Определение кристаллографических индексов гексагональных кристаллов.
- •Индексы направлений
- •Лекция 5 Формулы геометрической кристаллографии.
- •Кристаллографические проекции.
- •I. Сферические координаты.
- •II. Стереографические проекции.
- •IV. Гномонические проекции.
- •Лекция 6 Решетки Бравэ
- •Теорема.
- •Симметрия внутреннего строения.
- •Плоскость скользящего отражения.
- •Винтовые оси
- •Тетрагональные кристаллы
- •Понятие о пространственной системе точек
- •Правила записи символа пространственной группы.
- •Распределение пространственных групп по классам симметрии, сингониям и категориям.
- •Лекция 8 Основы кристаллохимии.
- •Объемные характеристики кристаллического материала
- •Факторы, влияющие на кристаллическую структуру
- •Понятие о плотнейших упаковках
- •Лекция 9
- •Типичные структуры материалов используемых в микроэлектронике.
- •Структурный тип магния.
- •Основные кристаллохимические характеристики
- •Полупроводниковые соединения
- •Основные кристаллохимические характеристики
- •Лекция 11
- •Структурный тип поваренной соли (NaCl).
- •Структура цезий хлор (СsCl).
- •Структурный тип халькопирита (CuFeS2)
- •Лекция 12 Структурный тип перовскита
- •Кристаллическая структура SiO2.
- •Кристаллическая структура Al2o3.
- •Лекция 13 Полиморфизм, изоморфизм и политипия.
- •Неустойчивая устойчивая
- •Классификация полиморфных модификаций по Бюргеру
- •Классификация изоструктурных соединений пр Гримму.
- •Лекция 14 Кристаллофизика
- •Предельные группы симметрии (группы Кюри)
- •Принцип суперпозиции Кюри
- •Указательная поверхность
- •Системы координат
- •Лекция 15 Скалярные и векторные свойства кристаллов.
- •Физические свойства кристаллов, описываемых тензором второго ранга.
- •Геометрические свойства указательной поверхности.
- •Лекция 16 Оптические свойства кристаллов Двупреломление лучей
- •Дефекты в кристаллических материалах
- •Точечные дефекты
- •Межузельный атом
- •Примесные атомы
- •Комплексы точечных дефектов
- •Лекция 17
- •Дефект Френкеля (сложный).
- •Механизм Шотке или образование тепловых вакансий (при нагревании).
- •Термодинамика точечных дефектов.
- •Линейные дефекты.
- •Понятие о векторе Бюргерса.
- •Лекция 18
- •Взаимодействие дислокаций между собой
- •Метод селективного травления
- •Лекция 19
- •Методика прогнозирования формы ямки травления.
- •Двумерные дефекты (поверхностные).
- •Модели, объясняющие высокоугловые границы.
- •Дефекты упаковки (ду).
Теорема.
В решетке всегда имеются трансляции, параллельные осям и плоскостям симметрии, а также трансляции, перпендикулярные к упомянутым элементам симметрии.
Если узлы располагаются по вершинам элементарного параллелепипеда повторяемости, то это примитивнаяэлементарная ячейка. (Р)
Базоцентрированная (бокоцентрированная)элементарная ячейка (А, В или С) — узлы располагаются в серединах параллельных граней: верхней и нижней — базоцентрированная, боковых — бокоцентрированная.
Оъемноцентрированные (I)
Гранецентрированные (F)
Таблица 1
|
Сингония |
Тип решетки |
|
авс
Моноклинная авс ==900
Ромбическая авс ===900
|
Р С
I F |
В
 сего
к низшей категории относится 7 типов
решетки.
сего
к низшей категории относится 7 типов
решетки.
|
а=вс ==900 =1200 Подсингония: ромбоэдрическая а=в=с ===900
Тетрагонгальная а=вс ===900
Гексагональная а=вс ==900 =1200
|
P (R)
Р I
Р |
В средней категории 4 типа решеток Бравэ.
|
а=в=с ===900
|
Р I
F |
К высшей категории относится 3 типа решеток Бравэ.
Совокупность координат узлов, входящих в элементарную ячейку, называют базисомячейки.
Симметрия внутреннего строения.
Для внешней формы, как упоминалось раньше, существует 8 независимых элементов симметрии. Для внутреннего строения добавляются следующие симметрические операции:
Трансляция (элементарный параллельный перенос без поворота).
Элементы симметрии — узел, ряд, сетка.
Скользящее отражение
Элементы симметрии — плоскости скользящего отражения. Всего их 5: a, b, c, n, d.
Винтовое движение.
Элементы симметрии — винтовые оси (двойные, тройные, четверные, шестерные).
Эти симметрические операции вводятся для бесконечныхфигур.
Плоскость скользящего отражения.
а
рис.1
Если скользящее отражение происходит вдоль оси Х, то это плоскость а, по оси У —в, по оси Z —с.
Пример для типа а
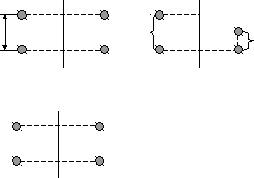 ОХ
ОХ
Т Т
t=½Т
Р а
а) б)
Рис.2
Пример для типа с
½
½ —поднятие происходит на эту высоту.
С
Эти плоскости обладают поступаниями (компонентами скольжения), действующими параллельно кристаллографическим осям.
П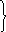 о
осям: Х — ½ а
о
осям: Х — ½ а
У — ½ в величины поступаний, где а, в, с — элементарные
Z — ½ c трансляции или типы плоскостей.
У плоскоcтей n и d компоненты скольжения (поступания) направлены по диагоналям сторон элементарной ячейки и равны их половинам и четвертям.
Для n: ½ (а+в) Для d: ¼ (а+в)
½ (в+с) ¼ (в+с)
½ (а+с) ¼ (а+с)
Пример
NaCl — поваренная соль.
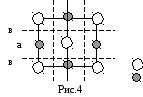 в
в
(100)
а=в
— Cl
а Р а — Na
Здесь плоскости скользящего отражения чередуются с обыкновенными плоскостями симметрии.










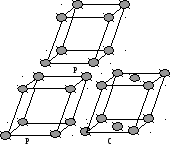 Триклинная
Триклинная Тригональная
Тригональная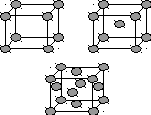 Кубическая
Кубическая