Принцип суперпозиции Кюри

Если различные внешние явления или воздействия накладываются друг на друга, образуя единую систему, то их дисимметрии складываются и остаются лишь общие элементы симметрии.

Пример

Куб

Было:3L₄4L₃6L₂9PC

Воздействие: L_Р

L_ L₃

L₂

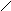
L₄ [001]

Результирующая симметрия будет разная, в зависимости от того, вдоль какой оси приложено воздействие, в данном случае, L₄

Стало: L₄4Р, остальные элементы симметрии исчезли.

Стереографическая проекция результата

Указательная поверхность

Для наглядного представления симметрии и анизотропии свойства пользуются указательной поверхностью, радиус-векторы которой характеризуют относительные величины свойства в данном направлении.

Для построения указательной поверхности:

1. Измеряют значение величин, определяющих анизотропное свойство кристалла по всем возможным направлениям.

2. Откладывают эти значения на радиус-векторах, исходящих из какой-либо точки внутри кристалла, выбранной за начало координат.

3. Соединяют концы этих векторов.

Симметрия физического свойства, а, следовательно, и указательной поверхности, может быть выше, чем симметрия кристалла (принцип Нейнмана), но при этом симметрия указательной поверхности должна содержать в себе симметрию кристалла.

Системы координат

Вкристаллографии: z

y

х

Углы любые

В кристаллофизике:

х₃

х₂

х₁

Всегда правая и ортогональная

Они совпадают для кубических, ромбических и тетрагональных кристаллов.

Одно и то же явление может быть выражено различными уравнениями, вид которых зависит от системы координат. При этом всегда надо знать, как преобразуется физическое свойство при переходе от одной системы координат к другой.

Вследствие анизотропии свойств кристаллов явление, вызванное в кристалле каким-либо воздействием, может не совпадать по направлению с этим воздействием, поэтому взаимосвязь свойства, воздействия и явления выражаются уравнением:

явление(эффект)=свойство*воздействие (1)

Лекция 15 Скалярные и векторные свойства кристаллов.

Скалярное свойство не зависит от направления, изотропно, обладает максимальной симметрией, и указательная поверхность скалярного свойства это сфера.

1. плотность;

2. объемный коэффициент теплового расширения;

3. коэффициент теплового сжатия;

4. теплоемкость.

Векторные свойства зависят от направления.

явление = свойство*воздействие

Определяются по координатам X₁, X₂, X₃.

Пусть у нас стоит задача осуществить переход к новой системе координат.

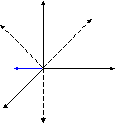X₃

X^’₂

X^’₃

AX₂

X₁

X^’₁

A– вектор в координатах X₁, X₂, X₃.

При переходе из одной системы координат в другую (X₁, X₂, X₃X^’₁, X^’₂, X^’₃) скалярные свойства не меняются.

явление = свойство*воздействие

(вектор) (вектор)(скаляр)

Свойство определяется компонентами вектора по трем осям или тензором первого ранга.

3¹=3

3^р, где р – ранг тензора – число компонент.

3²=9; 3³=27.

При переходе X₁, X₂, X₃X^’₁, X^’₂, X^’₃( повернутой на угол) нужно преобразовать векторную велечину по закону косинуса и это имеет вид:

А^’_i=c_ikA_k

A_k=(A₁,A₂,A₃); i,k=1,2,3…

c_ik- косинус между старой и новой системой координат:

с_ik=cos(X^’_iX_k)

i– относится к новой системе координат, ак– к старой.

A^’₁=A₁cos(X^’₁X₁) + A₂cos(X^’₁X₂) + A₃cos(X^’₁X₃) = c₁₁A₁+c₁₂A₂+c₁₃A₃

Это равенство можно представить в виде таблицы косинусов.

	X1	X2	X3
X’1	C11	C12	C13
X’2	C21	C22	C23
X’3	C31	C32	C33

По этой таблице определяются коэффициенты при переходе от одной системе к другой.

Для изучения физического свойства кристалла сначала устанавливают изотропно или анизотропно свойство. Если свойство анизотропно, то надо установить ранг тензора и его связь с симметрией кристалла.

Компоненты тензора определяются по матричной формуле. Если у нас 3²=9 – это обычный вектор, который определяется девятью фактическими компонентами (их нужно определить). Компоненты тензора второго ранга a_ijопределяются:

a₁₁a₁₂a₁₃

a_ij= a₂₁a₂₂a₂₃3²=9

a₃₁a₃₂a₃₃

Пироэлектрический эффект– это явление, которое присуще и состоит в способности изменять величину

явление = свойство*воздействие

При нагревании или охлаждении кристаллов на его гранях появляется заряд противоположных знаков.

n ps

 ps – вектор спонтанной поляризации.



=Р²_i*n_i= |P²|cos,

n – единичный вектор;



При равномерном распределении температуры происходит изменение вектора спонтанной поляризации, который определяется величиной коэффициента - вектор пироэлектрических коэффициентов.

рs=T(₁,₂,₃)

 - положителен, если возрастание температуры приводит к возрастанию спонтанной поляризации.

Пироэлектрический эффект может наблюдаться не во всех кристаллах, а только в кристаллах десяти классов, у которых есть единичное направление.

Указательная поверхность пироэлектрического эффекта:

+ Две сферы, разделенных плос-

костью антисимметрии (плос-

кость меняет знак на противопо-

ложный) - m

m

-

Если использовать антисимметрию:

Если было 32 точечные группы, то будет 58.

Эффект, обратный пироэлектрическому – электрокалорический – действие электрического поля вызывает изменение температуры кристалла и фиксируется с точностью 10^-90С.