
- •Лекция 1
- •Лекция 2
- •Отражение
- •Вращение
- •Инверсия
- •Отражение-вращение
- •Вращение-инверсия
- •Взаимодействие элементов симметрии (теоремы сложения).
- •Теорема №1
- •Обратная теорема
- •Виды симметрии кристаллов.
- •Виды симметрии кристаллов, обладающих единичным направлением.
- •Виды симметрии кристаллов без единичных направлений.
- •Лекция 4 Характеристика сингоний.
- •Обозначение плоскостей и направлений в кубических кристаллах.
- •Порядок нахождения индексов плоскостей.
- •Аспекты эквивалентности плоскостей.
- •Индексы направлений.
- •Алгоритм определения индексов направлений.
- •Определение кристаллографических индексов гексагональных кристаллов.
- •Индексы направлений
- •Лекция 5 Формулы геометрической кристаллографии.
- •Кристаллографические проекции.
- •I. Сферические координаты.
- •II. Стереографические проекции.
- •IV. Гномонические проекции.
- •Лекция 6 Решетки Бравэ
- •Теорема.
- •Симметрия внутреннего строения.
- •Плоскость скользящего отражения.
- •Винтовые оси
- •Тетрагональные кристаллы
- •Понятие о пространственной системе точек
- •Правила записи символа пространственной группы.
- •Распределение пространственных групп по классам симметрии, сингониям и категориям.
- •Лекция 8 Основы кристаллохимии.
- •Объемные характеристики кристаллического материала
- •Факторы, влияющие на кристаллическую структуру
- •Понятие о плотнейших упаковках
- •Лекция 9
- •Типичные структуры материалов используемых в микроэлектронике.
- •Структурный тип магния.
- •Основные кристаллохимические характеристики
- •Полупроводниковые соединения
- •Основные кристаллохимические характеристики
- •Лекция 11
- •Структурный тип поваренной соли (NaCl).
- •Структура цезий хлор (СsCl).
- •Структурный тип халькопирита (CuFeS2)
- •Лекция 12 Структурный тип перовскита
- •Кристаллическая структура SiO2.
- •Кристаллическая структура Al2o3.
- •Лекция 13 Полиморфизм, изоморфизм и политипия.
- •Неустойчивая устойчивая
- •Классификация полиморфных модификаций по Бюргеру
- •Классификация изоструктурных соединений пр Гримму.
- •Лекция 14 Кристаллофизика
- •Предельные группы симметрии (группы Кюри)
- •Принцип суперпозиции Кюри
- •Указательная поверхность
- •Системы координат
- •Лекция 15 Скалярные и векторные свойства кристаллов.
- •Физические свойства кристаллов, описываемых тензором второго ранга.
- •Геометрические свойства указательной поверхности.
- •Лекция 16 Оптические свойства кристаллов Двупреломление лучей
- •Дефекты в кристаллических материалах
- •Точечные дефекты
- •Межузельный атом
- •Примесные атомы
- •Комплексы точечных дефектов
- •Лекция 17
- •Дефект Френкеля (сложный).
- •Механизм Шотке или образование тепловых вакансий (при нагревании).
- •Термодинамика точечных дефектов.
- •Линейные дефекты.
- •Понятие о векторе Бюргерса.
- •Лекция 18
- •Взаимодействие дислокаций между собой
- •Метод селективного травления
- •Лекция 19
- •Методика прогнозирования формы ямки травления.
- •Двумерные дефекты (поверхностные).
- •Модели, объясняющие высокоугловые границы.
- •Дефекты упаковки (ду).
Винтовые оси
=3600/n — одинарные.
21— двойные (поворот на 1800и подъем на ½ элементарной трансляции).
31, 32— тройные (поворот на 1200и поворот на 1/3 или 2/3 элементарной трансляции).
41, 42, 43— четверные.
61, 62, 63, 64, 65— шестерные.
Подстрочный индекс: t=T/n, где T — величина трансляции, n — порядок оси.
Винтовые оси бывают левые и правые, либо и левые, и правые одновременно.
Пример

½ Т
2
Тетрагональные кристаллы
5 4
Т 3
2
1
рис.6
Это четверная правая ось 41(поступание ¼ ), поскольку закручивание идет по часовой стрелке, если смотреть снизу .
Если закручивание идет против часовой стрелки, если смотреть снизу , то ось левая.
К омбинируя
восьми элементов симметрии внешней
формы конечных фигур и элементов
симметрии внутренней формы бесконечных
фигур, получаем 230пространственныхгрупп (32 точечные группы 230
пространственных групп).
омбинируя
восьми элементов симметрии внешней
формы конечных фигур и элементов
симметрии внутренней формы бесконечных
фигур, получаем 230пространственныхгрупп (32 точечные группы 230
пространственных групп).
Пространственная группа— совокупность всех элементов симметрии кристаллической структуры.
Понятие о пространственной системе точек
Любая точка, повторенная элементами симметрии пространственной группы, приводит к правильной системе точек.
Правильной системой точек называется система точек, выводящихся из исходной точки посредством элементов симметрии пространственных групп.
Правильная система точек для каждой пространственной группы выражает геометрические законы пространственного расположения структурных единиц в кристалле.
Лекция 7
Место нахождения исходной точки это ее позиция. Число точек системы, приходящихся на одну элементарную систему, называется кратностью системы. Если точка не находится не на одном из закрытых элементов симметрии, ее позиция называется общей. Если же находится – частной. Кратность частной меньше в целое число раз общей позиции.
230 пространственных групп симметрии.
Пространственной группой называется сочетание всех возможных преобразований симметрии в кристаллической структуре.
Каждой точечной группе соответствует несколько пространственных групп.
В 1890-1894 гг. Федоров, Шенфлис вывели 230 пространственных групп.
Классификационная схема пространственных групп симметрии.
В качестве определяющего признака принято использовать порядок оси, либо метрику трансляционной группы.
Н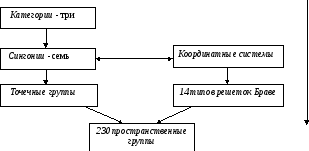 а
основе порядка На основе
метрики
а
основе порядка На основе
метрики
оси трансляционной группы
детализация
признаков
Международные символы точечных групп.
Пишутся только порождающие элементы симметрии ( предпочтение отдается плоскостям).
n – ось n-го порядка;
_
n – инверсионная ось n-го порядка;
m – плоскость симметрии;
nm – ось симметрии n-го порядка и m плоскостей симметрии проходящих через нее;
n/m – ось симметрии n-го порядка и плоскость симметрии ей перпендикулярная;
n2 – ось симметрии n-го порядка и n осей второго порядка, которые будут перпендикулярны ей;
n/m*m – ось симметрии n-го порядка, плоскость ей перпендикулярная и плоскость ей параллельная.
Важно соблюдать правило установки кристаллов и порядок записи. При этом различают «координатные» элементы симметрии, проходящие вдоль координатной плоскости и «диагональные», проходящие по биссектрисам углов между ними.
Пример, средняя категория
L66P
6m
1 позиция – главная ось;
2 позиция – координатные элементы симметрии;
3 позиция – диагональные элементы симметрии.
