Взаимодействие дислокаций между собой

1. Если дислокации одного знака находятся в одной плоскости скольжения, они стремятся разойтись.



2. Если дислокации разного знака находятся в одной плоскости скольжения, то происходит их аннигиляция и уничтожение.



3. Если дислокации одного знака находятся в параллельных плоскостях скольжения, они могут выстраиваться друг под другом, образуя стенку дислокаций.







4. Если дислокации разного знака находятся в параллельных плоскостях скольжения, они могут выстраиваться под углом 45⁰.



45⁰

5. Дислокации взаимодействуют с точечными дефектами, являются их стоками.

Здесь действуют

упругие поля нап атмосфера Котрелла

ряжений, происх

одит притягиван

ие

дислокация точечные дефекты

Точечные дефекты затрудняют движение дислокации (являются стопорами).

6. Дислокации (только сидячие) могут размножаться.

У сидячих дислокаций концы закреплены. Источник этих дислокаций предложен Франком Ридом в 1950 году.

Под действием приложенного однородного напряжения происходит изгибание линии дислокации, а линейное напряжение дислокации будет стремиться ее выпрямить.

b

D D^/

=Gb/r

r — радиус изгибания дуги дислокации

G — модуль сдвига

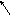
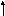
=0,51,0

D D^/

Штриховкой показана площадь, через которую постепенно продвигается линия дислокации.

r=l/2

l — длина дислокации

_кр=Gb/l (при=1/2) — критическое значение

При <_кр — дуга стабильна

При _кр площадь растет:

b

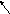
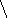
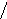
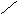
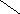D D^/

Приложенная сила всегда перпендикулярна линии дислокации.

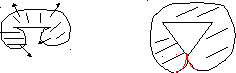
D D^/

C

В конце концов на стыке образуются дислокации разного знака (красная линия), DD^/C стремится выпрямиться и занять положение DD^/, а петля уходит в кристалл.

Такой источник Франка Рида может генерировать неограниченное число петель дислокаций в одной плоскости скольжения и может создать в ней значительный сдвиг.

Метод селективного травления

N_Д — плотность дислокаций [1/см²]

Средняя N_Д=10² 10⁷ 1/см²

Для каждого материала подбирается свой травитель, так, чтобы скорость травления по поверхности относилась к скорости травления по дислокациям как10

V_Д/V_n10 V_n

V_Д

В местах выхода дислокаций на поверхность образуются ямки травления, они имеют правильную геометрическую форму и ограняются наиболее плотно упакованными плоскостями (d*max)

1 2 3 4

1. Тетрагональная пирамида, уходящая вглубь

2. Лодочка

3. Копье

4. Трапеция

Круглой формы быть не может, так как при травлении растворяются плоскости, у которых d*_(hkl) минимальна.

Форма ямки травления зависит от двух факторов:

1. От вида и структуры кристаллического материала

2. От плоскости шлифа, по которой разрезают монокристалл

ПК, NaCl d*_max{100}, в совокупность входит шесть плоскостей, значит это гексаэдр.

ГЦК, алмаз (сфалерит) d*_max{111}, в совокупность входит восемь плоскостей, значит это октаэдр.