
- •Пояснительная Записка
- •1 Введение 6
- •5.3 Расчет 117
- •Введение
- •Исследовательская часть
- •Структура подсистемы защиты информации в системе глобальной спутниковой связи и методы обеспечения средств мониторинга и управления объектами защиты информации
- •Описание среды комплекса спутниковой глобальной радиосвязи и выявление целей защиты информации
- •Состав и структура подсистемы защиты информации в комплексе спутниковой глобальной радиосвязи.
- •Прослушивание второго рода, как метод построения эффективных атак на систему связи.
- •Алгоритм массирования – как метод защиты от прослушивания второго рода.
- •Линейные кодовые последовательности.
- •Нелинейные кодовые последовательности.
- •Однократное гаммирование.
- •Требования к алгоритму маскирования.
- •Специальная часть
- •Основные требования.
- •Соответствие предъявляемому уровню безопастности.
- •Построение на основе использования криптографии симметричных ключей.
- •Описание.
- •Математическое описание.
- •Описание параметров.
- •Формирование ключа.
- •Разворачивание ключа.
- •Определение времени жизни сеансовых ключей
- •Программная и аппаратная гибкость реализации
- •Оценка сложности программной и аппаратной реализации
- •Вычислительная сложность (скорость) зашифрования/расшифрования
- •Оценочное время выполнения зашифрования/расшифрования блока данных
- •Оценочная скорость алгоритма в виде числа тактов работы процессора
- •Скорость выполнения зашифрования/расшифрования блока данных
- •Пакет тестов Национального института стандартов и технологий (nist)
- •Частотный тест.
- •Тест на самую длинную серию единиц в блоке.
- •Тест ранга двоичных матриц.
- •Тест с дискретным преобразованием Фурье (спектральный тест).
- •Универсальный статистический тест Маурэра.
- •Сжатие при помощи алгоритма Лемпела-Зива.
- •Тест линейной сложности.
- •Результаты тестирования
- •Результаты проведения тестов
- •Спектральный тест
- •Тест линейной сложности
- •Технологический раздел
- •Введение
- •Общие принципы тестирования
- •Общие методики оценки качества алгоритма маскирования данных
- •Графические тесты
- •Гистограмма распределения элементов
- •Распределение на плоскости
- •Проверка серий
- •Проверка на монотонность
- •Оценочные тесты
- •Методы тестирования алгоритма маскирования данных
- •Система оценки статистических свойств
- •Оценка результатов тестирования
- •Генерация последовательностей для тестирования
- •Исполнение набора статистических тестов
- •Анализ прохождения статистических тестов
- •Организационно-экономический раздел
- •Введение
- •Теоретическая часть
- •Оценка затрат на разработку по
- •Составляющие затрат на программный продукт
- •Составляющие затрат на разработку программ Ср.
- •Затраты на непосредственную разработку кп
- •Сложность комплекса программ
- •Применение современных методов разработки кп.
- •Факторы организации процесса разработки кп, влияющие на непосредственные затраты при создании сложных программ.
- •Затраты на изготовление опытного образца как продукции производственно-технического назначения.
- •Затраты на технологию и программные средства автоматизации разработки комплекса программ.
- •Составляющие затрат на эксплуатацию программ, влияющие на процесс их разработки.
- •Исходные данные
- •Расчёт затрат
- •1)Составляющие затрат на разработку программ:
- •2) Затраты на эксплуатацию программ:
- •3) Накладные расходы
- •Производственно-экологическая безопасность
- •Введение
- •Машинный зал и рабочее место программиста
- •Вредные факторы, присутствующие на рабочем месте и их классификация
- •Вредные производственные воздействия
- •Электрическая опасность
- •Нерациональность освещения
- •Расчет искусственного освещения методом коэффициента использования светового потока
- •Психофизические факторы
- •Микроклимат
- •Посторонние шумы
- •Постороннее электромагнитное излучение
- •Химические факторы
- •Эргономические требования
- •Эргономика окружающей среды
- •Экологическая безопасность
- •Заключение
- •Литература
- •Приложение 1
- •Приложение 2
- •Приложение 3
Построение на основе использования криптографии симметричных ключей.
Симметричный алгоритм, иногда называемый условным алгоритмом, это тот, в котором ключ зашифрования может быть вычислен из ключа расшифрования, и наоборот.
В симметричном алгоритме ключи зашифрования и расшифрования одинаковы. Этот алгоритм, называемый также алгоритмом с секретным ключом или алгоритм с единым ключом, требует, чтобы отправитель и получатель перед началом передачи секретных сообщений согласовали используемый ключ. Защита, обеспечиваемая симметричным алгоритмом, определяется ключом; раскрытие ключа означает, что шифровать и расшифровывать сообщения сможет кто угодно. До тех пор, пока передаваемая информация должна оставаться тайной, ключ должен храниться в секрете.
Симметричные алгоритмы подразделяются на две категории. Одни алгоритмы обрабатывают открытый текст побитово. Такие алгоритмы потоковыми алгоритмами или потоковыми шифрами. Другие алгоритмы обрабатываю группы битов открытого текста . Эти группы называют блоками, а алгоритмы – блочными алгоритмами. Таким образом разрабатываемый мною алгоритм будет строится на основе блочных алгоритмов.
Описание.
Математическое описание.
Наиболее подходящими для реализации в компьютерных системах процедур маскирования являются блочные шифры разового пользования, т.е. шифры, ключевой оператор которых явно зависит от временного параметра t. Характер изменений этого параметра определяет временные интервалы «разового пользования» ключевым материалом.
Идея разового
пользования была сформирована в явном
виде в работе [2] на примере преобразования
Л.Хилла, где рассматривается аффинное
отображение
![]() на
на![]() (здесь
(здесь![]() - кольцо вычетов поmod
q
кольца целых чисел Z):
- кольцо вычетов поmod
q
кольца целых чисел Z):
y = Ktx + d, (3.1)
где элементы матрицы Ktзависят от временного параметраt.
Для обратимости отображения (3.1) требуется, чтобы выполнялось условие
НОД (det Kt, q) = 1 (3.2)
В такой постановке проблема разового пользования ключом сводится к задаче генерации квадратных матриц Kt, зависящих от параметраtи удовлетворяющих условию (3.2).
Для ее решения
были использованы инволютивные и
треугольные матрицы. Естественно
обобщить этот метод динамического (т.е.
зависящего от t)
и биективного отображения![]() на
на![]() ,
базируясь на генерации в каждый моментtслучайных матриц
над
,
базируясь на генерации в каждый моментtслучайных матриц
над![]() требуемых порядков. Назовем этот метод
обобщенным методом Хилла.
требуемых порядков. Назовем этот метод
обобщенным методом Хилла.
Сформируем сначала требования, предъявляемые к конструированию подобных отображений.
Первое требование:отображение должно удовлетворять принципу Хопфа.
В классической работе [3] К. Шеннон разработал ряд приемов построения кодирующих (и декодирующих) отображений, которые направлены на осложнение криптоанализа. Это, так называемые, методы распыления и зашумления, которые далее были синтезированы им в метод перемешивания. К. Шеннон отмечает, что к хорошему перемешиванию приводят не коммутирующие между собой процедуры (на примере исследований Е.Хопфа), а также методы, использующие операции разнотипных (т.е. несовместимых) алгебраических систем. Именно последние требования в настоящей работе названы принципом Хопфа.
Второе требование:компьютерная согласованность. Конструируемое отображение должно использовать типы и структуры данных, операции над которыми допускают реализацию в используемой вычислительной среде.
Третье требование:принцип гибкой динамичности. Конструируемое отображение должно обеспечивать в каждый момент времениtгибкое управление рандомизацией ключевого материала.
Известный в
вычислительной практике метод
Гаусса-Зейделя решения систем уравнений
подсказывает следующий прием построения
динамичного биективного отображения
![]() на
на![]() ,
удовлетворяющий перечисленным
требованиям.
,
удовлетворяющий перечисленным
требованиям.
1. Модуль qвыбирается в видеq= 2N, гдеN– длина регистров, используемой вычислительной среды. Предполагается, арифметический процессор обладает устройством умножения двухN-битных операндов с сохранением 2N-битного результата.
2. Генерируется
«материнская» случайная матрица над
![]() или
в более простом и более гибком случае
«псевдослучайная матрица» размерностиnn:
или
в более простом и более гибком случае
«псевдослучайная матрица» размерностиnn:

n*Nбит – размерность блока данных за один раунд маскирования (демаскирования).
3. Кодирующее (шифрующее) и декодирующее (дешифрующее) отображение формируется в форме Гаусса-Зейделя:
а)
y 1
= |x1
∦
a11x2
+ a12x3
+……………+a1,n-1xn
∦N
a1n
|2N;
1
= |x1
∦
a11x2
+ a12x3
+……………+a1,n-1xn
∦N
a1n
|2N;
y2 = |x2 ∦ a21x3 + a22x4 +……………+ a2,n-1y1 ∦N a2n |2N;
y3 = |x3 ∦ a31x4 + a32x5 +… a3,n-2y1 + a3,n-1y2 ∦N a3n |2N;
………………………………………………………………..
yn = |xn ∦ an1y1 + an2y2 +….. …+ an,n-1yn-1 ∦N ann |2N;
б)
y 1
= |x1
∦
a11x2
+ a12x3
+……………+
a1,n-1xn
∦N
a1n
|2N;
1
= |x1
∦
a11x2
+ a12x3
+……………+
a1,n-1xn
∦N
a1n
|2N;
y2 = |x2 ∦ a21x3 + a22x4 +……………+ a2,n-1y1 ∦N a2n |2N;
y3 = |x3 ∦ a31x4 + a32x5 +…+ a3,n-2y1 + a3,n-1y2 ∦N a3n |2N;
………………………………………………………………..
yn = |xn ∦ an1y1 + an2y2 +….. …+ an,n-1yn-1 ∦N ann |2N;
Здесь используются следующие обозначения:
| . |2N- операция взятия вычета поmod2N;
- операция побитого xor;
| a+b|2N, |a-b|2N- операции сложения и вычитания поmod2N;
ab– операция арифметического умножения двухN-разрядных целых чисел с формированием 2N-битного результата;
∦.∦N- операция перемешивания битов 2N-битного слова с получением в результатеN-битного слова по следующей схеме: из 2N-битного слова выделяется (псевдослучайно) блок изNбит, которые побитно перемножаются по модулю два с оставшимисяN-битами исходного 2N-битного слова.
Все используемые здесь операции не перестановочные и максимально приближены к программной реализации.
Алгоритмическая сложность этого типа преобразований, главным образом, определяется n(n-1) операциями над целыми числами и реализацией операции∦.∦N. Также свой вклад в алгоритмическую сложность вносят динамические преобразования ключевой материнской матрицы на каждом шаге кодирования.
Если требуется ослабить вычислительную сложность конструируемого отображения, то вместо операции арифметического умножения (а) можно использовать операцию побитого xor(б) целыхN-разрядных чисел. Также можно модифицировать операцию∦.∦N в операцию псевдослучайного считыванияN-битного блока из (N+1)-битного слова, в случае применения операций арифметического сложения. В этом случае ослабляется требование к размеру и способу формирования матрицы преобразования.
Гибкая динамичность в управлении ключевым материалом достигается за счет использования различных форм псевдослучайных перестановок элементов матрицы преобразования.
Для вычислительного эксперимента было сконструировано отображение где:
операция ∦.∦Nозначает операцию псевдослучайной выборкиNбит из 2N-битного слова;
создана материнская ключевая матрица со случайными элементами. На каждом раунде маскирования используется псевдослучайная перестановка ключевых элементов.
В рамках дипломного проекта было разработано программное обеспечение маскирование данных в соответствии с предложенным выше алгоритмом, удовлетворяющее требованиям технического задания, руководство оператора представлено в приложении 3. Схема алгоритма работы программного обеспечения маскирования данных представлено на рисунке 3.1
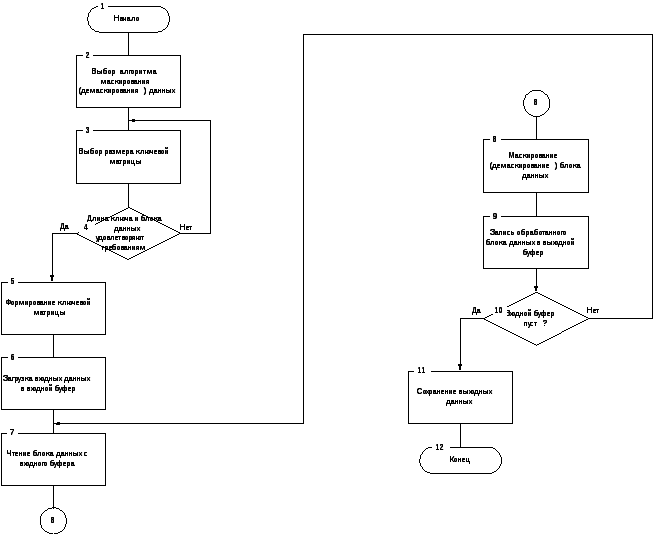
Рис 3.1. Схема алгоритма работы программного обеспечения маскирования данных
