- •Пояснительная Записка
- •1 Введение 6
- •5.3 Расчет 117
- •Введение
- •Исследовательская часть
- •Структура подсистемы защиты информации в системе глобальной спутниковой связи и методы обеспечения средств мониторинга и управления объектами защиты информации
- •Описание среды комплекса спутниковой глобальной радиосвязи и выявление целей защиты информации
- •Состав и структура подсистемы защиты информации в комплексе спутниковой глобальной радиосвязи.
- •Прослушивание второго рода, как метод построения эффективных атак на систему связи.
- •Алгоритм массирования – как метод защиты от прослушивания второго рода.
- •Линейные кодовые последовательности.
- •Нелинейные кодовые последовательности.
- •Однократное гаммирование.
- •Требования к алгоритму маскирования.
- •Специальная часть
- •Основные требования.
- •Соответствие предъявляемому уровню безопастности.
- •Построение на основе использования криптографии симметричных ключей.
- •Описание.
- •Математическое описание.
- •Описание параметров.
- •Формирование ключа.
- •Разворачивание ключа.
- •Определение времени жизни сеансовых ключей
- •Программная и аппаратная гибкость реализации
- •Оценка сложности программной и аппаратной реализации
- •Вычислительная сложность (скорость) зашифрования/расшифрования
- •Оценочное время выполнения зашифрования/расшифрования блока данных
- •Оценочная скорость алгоритма в виде числа тактов работы процессора
- •Скорость выполнения зашифрования/расшифрования блока данных
- •Пакет тестов Национального института стандартов и технологий (nist)
- •Частотный тест.
- •Тест на самую длинную серию единиц в блоке.
- •Тест ранга двоичных матриц.
- •Тест с дискретным преобразованием Фурье (спектральный тест).
- •Универсальный статистический тест Маурэра.
- •Сжатие при помощи алгоритма Лемпела-Зива.
- •Тест линейной сложности.
- •Результаты тестирования
- •Результаты проведения тестов
- •Спектральный тест
- •Тест линейной сложности
- •Технологический раздел
- •Введение
- •Общие принципы тестирования
- •Общие методики оценки качества алгоритма маскирования данных
- •Графические тесты
- •Гистограмма распределения элементов
- •Распределение на плоскости
- •Проверка серий
- •Проверка на монотонность
- •Оценочные тесты
- •Методы тестирования алгоритма маскирования данных
- •Система оценки статистических свойств
- •Оценка результатов тестирования
- •Генерация последовательностей для тестирования
- •Исполнение набора статистических тестов
- •Анализ прохождения статистических тестов
- •Организационно-экономический раздел
- •Введение
- •Теоретическая часть
- •Оценка затрат на разработку по
- •Составляющие затрат на программный продукт
- •Составляющие затрат на разработку программ Ср.
- •Затраты на непосредственную разработку кп
- •Сложность комплекса программ
- •Применение современных методов разработки кп.
- •Факторы организации процесса разработки кп, влияющие на непосредственные затраты при создании сложных программ.
- •Затраты на изготовление опытного образца как продукции производственно-технического назначения.
- •Затраты на технологию и программные средства автоматизации разработки комплекса программ.
- •Составляющие затрат на эксплуатацию программ, влияющие на процесс их разработки.
- •Исходные данные
- •Расчёт затрат
- •1)Составляющие затрат на разработку программ:
- •2) Затраты на эксплуатацию программ:
- •3) Накладные расходы
- •Производственно-экологическая безопасность
- •Введение
- •Машинный зал и рабочее место программиста
- •Вредные факторы, присутствующие на рабочем месте и их классификация
- •Вредные производственные воздействия
- •Электрическая опасность
- •Нерациональность освещения
- •Расчет искусственного освещения методом коэффициента использования светового потока
- •Психофизические факторы
- •Микроклимат
- •Посторонние шумы
- •Постороннее электромагнитное излучение
- •Химические факторы
- •Эргономические требования
- •Эргономика окружающей среды
- •Экологическая безопасность
- •Заключение
- •Литература
- •Приложение 1
- •Приложение 2
- •Приложение 3
Тест с дискретным преобразованием Фурье (спектральный тест).
Цель теста
Суть этого теста – высоты пиков в Дискретном Преобразовании Фурье тестируемой последовательности. Цель этого теста – обнаружить периодический характер тестируемой последовательности который бы указал на отклонение от предположения случайности. Наша цель – определить, будет ли число пиков, превышающих 95 %-ый порог существенно отличаться от 5 %.
Вызов функции
DiscreteFourierTransform(n), где:
n Длина строки бит.
Последовательность бит, вырабатываемая генератором случайных чисел, который тестируется; = 1, 2, … , n.
Тестовая статистика и распределение.
d: Нормированная разность между наблюдаемым и ожидаемым числом частотных компонент, которые выше 95%-ого порога.
Соответствующее распределение для тестовой статистики – нормальное распределение.
Описание теста
(1) Нули и единицы входной последовательности (ε) заменяются значениями –1 и +1 соответственно. В результате получается последовательность X = x1, x2, …, xn, где
xi = 2εi – 1.
Например, если n = 10 и ε = 1001010011, то X = 1, -1, -1, 1, -1, 1, -1, -1, 1, 1.
(2) Вектор X подвергается Дискретному Преобразованию Фурье (DFT): S = DFT(X). Получится последовательность комплексных переменных, которая представляет периодические компоненты последовательности бит в разных частотах. (смотри в пункте 6 образец диаграммы DFT).
(3) Вычисляются M = modulus(S´) |S'|, где S´ - это подстрока, состоящая из первых n/2
элементов в S, и функция модуля образует последовательность пиковых высот.
(4) Вычисляем T
=![]() =
95 %-ое пороговое значение пиковой высоты.
Для того, чтобы последовательность была
случайной, 95 % значений, полученных при
тестировании не должны превышать T.
=
95 %-ое пороговое значение пиковой высоты.
Для того, чтобы последовательность была
случайной, 95 % значений, полученных при
тестировании не должны превышать T.
(5) Вычисляем N0
=0 .95![]() .
N0
– это ожидаемое теоретическое (95 %) число
пиков (в предположении случайности)
которое меньше T.
.
N0
– это ожидаемое теоретическое (95 %) число
пиков (в предположении случайности)
которое меньше T.
Для нашего примера, N0 = 4.75.
(6) Вычисляем N1 = действительное наблюдаемое число пиков в M , которые меньше T.
Для нашего примера, N1 = 4.
(7) Вычисляем
![]() .
.
Для
нашего примера,
![]()
(8)
Вычисляем P-значение
= erfc![]() .
.
Для
нашего примера, P-значение
= erfc![]() .
.
Правило принятия решения (1%- уровень)
Если вычисленное P-значение < 0.01, то считаем, что последовательность неслучайна. В противном случае, считаем, что последовательность случайна.
Выводы и интерпретация результатов.
Т.к. вычисленное на шаге 8 пункта 4 P-значение 0.01 (P-значение = 0.123812), делаем вывод, что последовательность случайна.
Слишком маленькое значение d указывало бы на слишком маленькое число пиков (< 95 %) ниже T, и слишком большое число пиков (больше 5 %) выше T.
Рекомендации
Рекомендуется для тестирования брать последовательности длиной n≥1000 бит.
Универсальный статистический тест Маурэра.
Цель теста
Суть этого теста – число бит между соответствующими шаблонами (мера, которая относится к длине сжатой последовательности). Цель этого теста – определить, может или нет последовательность быть сильно сжата без потери информации. Сильно сжимаемые последовательности относятся к неслучайным.
Вызов функции
Universal(L, Q, n), где :
L Длина каждого блока. Замечание: использование L в качестве размера блока не соответствует обозначению размера блока (M) используемому в других тестах. Однако, использование L в качестве размера блока было указано в оригинальном источнике теста Маурэра.
Q Число блоков в первоначальной последовательности.
n Длина строки бит.
Последовательность бит, вырабатываемая генератором случайных чисел, который тестируется; = 1, 2, … , n.
Тестовая статистика.
fn : Сумма log2 расстояний между соответствующими L-битными образцами, т.е., сумма числа цифр в расстоянии между L-битными образцами.
Соответствующее распределение для тестовой статистики – это полунормальное распределение (односторонний вариант нормального распределения), которое описано в пункте 1.3.
Описание теста
(1) n-битная последовательность (ε) делится на два сегмента : начальный сегмент,
состоящий из Q L-битных непересекающихся блоков, и тестовый сегмент, состоящий из K L-битных непересекающихся блоков. Биты, оставшиеся в конце последовательности, которые не составляют целый L-битный блок, отбрасываются.

Первые Q
блоков
используются для инициализации теста.
Оставшиеся K
блоков –
тестовые блоки (K
=![]() ).
).
Например, если ε = 01011010011101010111, то n = 20. Если L = 2 и Q = 4, то K
=
![]() =
=
![]() =
6. Начальный
сегмент: 01011010; тестовый сегмент:
011101010111. L-битные
блоки показаны в таблице 3.7:
=
6. Начальный
сегмент: 01011010; тестовый сегмент:
011101010111. L-битные
блоки показаны в таблице 3.7:
Табл. 3.7 L-битные блоки.

(2) Используя начальный сегмент, создаём таблицу для каждого возможного L-битного значения (т.е., L-битное значение используется в качестве индекса в таблице). Номер блока последнего местоположения каждого L-битного блока записывается в таблицу (т.е., для i от 1 до Q, Tj= i, где j – десятичное представление содержания i-ого L-битного блока).
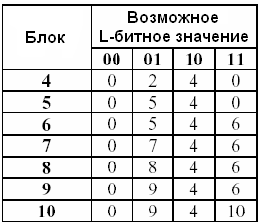
Для нашего примера создана таблица 3.8 с помощью 4х начальных блоков:
Табл. 3.8 Последнее местоположение каждого L-битного блока.

(3) Просматриваем каждый из K блоков в тестовом сегменте и определяем номер блоков после последнего местоположения того же самого L-битного блока (т.е., i – Tj). Заменяем значение в таблице положением текущего блока (т.е., Tj= i). Прибавляем вычисленное расстояние между местоположениями того же L-битного блока к накопленной сумме log2 всех разниц, определённых в K блоках (т.е., sum = sum + log2(i – Tj)).
Для нашего примера, таблица (см. табл. 3.9) и накопленная сумма выводятся следующим образом:
Для 5-ого блока : 5 расположена в “01” строке таблицы (т.е. T1),
и sum=log2(5-2) = 1.584962501.
Для 6-ого блока : 6 расположена в “11” строке таблицы (т.е., T3), и sum =
1.584962501 + log2(6-0) = 1.584962501 + 2.584962501 = 4.169925002.
Для 7-ого блока : 7 расположена в “01” строке таблицы (т.е., T1), и sum =
4.169925002 + log2(7-5) = 4.169925002 + 1 = 5.169925002.
Для 8-ого блока : 8 расположена в “01” строке таблицы (т.е., T1), и sum =
5.169925002 + log2(8-7) = 5.169925002 + 0 = 5.169925002.
Для 9-ого блока : 9 расположена в “01” строке таблицы (т.е., T1), и sum =
5.169925002 + log2(9-8) = 5.169925002 + 0 = 5.169925002.
Для 10-ого блока: 10 расположена в “11” строке таблицы (т.е., T3), и sum =
5.169925002 + log2(10-6) = 5.169925002 + 2 = 7.169925002.
Состояния таблицы:
Табл.3.9 Последнее местоположение каждого L-битного блока в тестовом сегменте.
(4) Вычисляем
тестовую статистику:
![]() ,
где
,
где![]() - запись таблицы, соответствующая
десятичному представлению содержанияi-ого
L-битного
блока.
- запись таблицы, соответствующая
десятичному представлению содержанияi-ого
L-битного
блока.
Для нашего примера,
![]()
(5) Вычисляем
P-значение =
erfc![]() ,
где ожидаемоеЗначение(L)
и
,
где ожидаемоеЗначение(L)
и
![]() берутся из таблицы 3.10:
берутся из таблицы 3.10:
Табл.3.10 Выбор ОжидаемогоЗначения и отклонения.

В предположении
случайности, значение ожидаемоеЗначение(L)
– теоретически-ожидаемое значение
вычисленной статистики для данной
L-битной
длины. Теоретическое стандартное
отклонение задаётся
![]() , где
, где![]() .
.
Для нашего примера,
P-значение =
erfc![]()
Заметим, что ожидаемое значение и отклонение (variance) для L = 2 не предусмотрены в вышеприведённой таблице, т.к. блок длиной два бита не рекомендуется брать для теста. Однако, это значение L принято в примере для простоты. Значения для ожидаемого значения и отклонения для случая, когда L=2, хоть и не приведены в вышеприведённой таблице, но взяты из книги “Handbook of Applied Cryptography.”
Правило принятия решения (1%- уровень)
Если вычисленное P-значение < 0.01, то считаем, что последовательность неслучайна. В противном случае, считаем, что последовательность случайна.
Выводы и интерпретация результатов.
Т.к. вычисленное на шаге 5 пункта 4 P-значение0.01 (P-значение = 0.767189), делаем вывод, что последовательность случайна.
Теоретические
ожидаемые значения для
![]() были вычислены, как показано в таблице
на шаге 5 пункта 4. Еслиfn
существенно
отличается от ожидаемогоЗначения(L),
то последовательность сильно сжимаема.
были вычислены, как показано в таблице
на шаге 5 пункта 4. Еслиfn
существенно
отличается от ожидаемогоЗначения(L),
то последовательность сильно сжимаема.
Рекомендации
Этот тест требует
длинную последовательность бит (n
≥
(Q
+ K)L),
которая делится на два сегмента L-битных
блоков, где L
должно быть
выбрано таким, что 6
≤
L
≤
16.
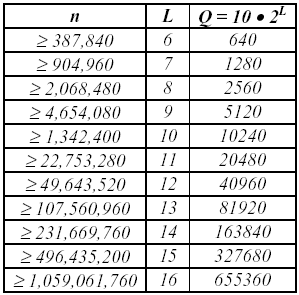
Первый сегмент состоит из Q
начальных
блоков, где Q
должно быть
выбрано таким, что Q
=
![]() .
Второй
сегмент состоит из K
тестовых блоков, где K
=
.
Второй
сегмент состоит из K
тестовых блоков, где K
=![]() .
Значения L,
Q
и n
должны
выбираться следующим образом:
.
Значения L,
Q
и n
должны
выбираться следующим образом:
Табл.3.11 Выбор значений L, Q и n.