
- •Пояснительная Записка
- •1 Введение 6
- •5.3 Расчет 117
- •Введение
- •Исследовательская часть
- •Структура подсистемы защиты информации в системе глобальной спутниковой связи и методы обеспечения средств мониторинга и управления объектами защиты информации
- •Описание среды комплекса спутниковой глобальной радиосвязи и выявление целей защиты информации
- •Состав и структура подсистемы защиты информации в комплексе спутниковой глобальной радиосвязи.
- •Прослушивание второго рода, как метод построения эффективных атак на систему связи.
- •Алгоритм массирования – как метод защиты от прослушивания второго рода.
- •Линейные кодовые последовательности.
- •Нелинейные кодовые последовательности.
- •Однократное гаммирование.
- •Требования к алгоритму маскирования.
- •Специальная часть
- •Основные требования.
- •Соответствие предъявляемому уровню безопастности.
- •Построение на основе использования криптографии симметричных ключей.
- •Описание.
- •Математическое описание.
- •Описание параметров.
- •Формирование ключа.
- •Разворачивание ключа.
- •Определение времени жизни сеансовых ключей
- •Программная и аппаратная гибкость реализации
- •Оценка сложности программной и аппаратной реализации
- •Вычислительная сложность (скорость) зашифрования/расшифрования
- •Оценочное время выполнения зашифрования/расшифрования блока данных
- •Оценочная скорость алгоритма в виде числа тактов работы процессора
- •Скорость выполнения зашифрования/расшифрования блока данных
- •Пакет тестов Национального института стандартов и технологий (nist)
- •Частотный тест.
- •Тест на самую длинную серию единиц в блоке.
- •Тест ранга двоичных матриц.
- •Тест с дискретным преобразованием Фурье (спектральный тест).
- •Универсальный статистический тест Маурэра.
- •Сжатие при помощи алгоритма Лемпела-Зива.
- •Тест линейной сложности.
- •Результаты тестирования
- •Результаты проведения тестов
- •Спектральный тест
- •Тест линейной сложности
- •Технологический раздел
- •Введение
- •Общие принципы тестирования
- •Общие методики оценки качества алгоритма маскирования данных
- •Графические тесты
- •Гистограмма распределения элементов
- •Распределение на плоскости
- •Проверка серий
- •Проверка на монотонность
- •Оценочные тесты
- •Методы тестирования алгоритма маскирования данных
- •Система оценки статистических свойств
- •Оценка результатов тестирования
- •Генерация последовательностей для тестирования
- •Исполнение набора статистических тестов
- •Анализ прохождения статистических тестов
- •Организационно-экономический раздел
- •Введение
- •Теоретическая часть
- •Оценка затрат на разработку по
- •Составляющие затрат на программный продукт
- •Составляющие затрат на разработку программ Ср.
- •Затраты на непосредственную разработку кп
- •Сложность комплекса программ
- •Применение современных методов разработки кп.
- •Факторы организации процесса разработки кп, влияющие на непосредственные затраты при создании сложных программ.
- •Затраты на изготовление опытного образца как продукции производственно-технического назначения.
- •Затраты на технологию и программные средства автоматизации разработки комплекса программ.
- •Составляющие затрат на эксплуатацию программ, влияющие на процесс их разработки.
- •Исходные данные
- •Расчёт затрат
- •1)Составляющие затрат на разработку программ:
- •2) Затраты на эксплуатацию программ:
- •3) Накладные расходы
- •Производственно-экологическая безопасность
- •Введение
- •Машинный зал и рабочее место программиста
- •Вредные факторы, присутствующие на рабочем месте и их классификация
- •Вредные производственные воздействия
- •Электрическая опасность
- •Нерациональность освещения
- •Расчет искусственного освещения методом коэффициента использования светового потока
- •Психофизические факторы
- •Микроклимат
- •Посторонние шумы
- •Постороннее электромагнитное излучение
- •Химические факторы
- •Эргономические требования
- •Эргономика окружающей среды
- •Экологическая безопасность
- •Заключение
- •Литература
- •Приложение 1
- •Приложение 2
- •Приложение 3
Сжатие при помощи алгоритма Лемпела-Зива.
Цель теста
Суть этого теста – число савокупно-определённых образцов (слов) в последовательности. Цель этого теста – определить, как сильно тестируемая последовательность может быть сжата. Последовательность принимается неслучайной, если она может быть существенно сжата. Случайная последовательность будет иметь характерное число определённых образцов.
Вызов функции
LempelZivCompression(n), где:
n Длина строки бит.
Последовательность бит, вырабатываемая генератором случайных чисел, который тестируется; = 1, 2, … , n.
Тестовая статистика.
Wobs: Число разъединённых и савокупно-определённых слов в последовательности.
Соответствующее распределение для тестовой статистики – нормальное распределение.
Описание теста
(1) Делаем «грамматический разбор» последовательности в последовательные, разъединённые и определённые слова, которые будут образовывать «словарь» слов в последовательности. Это заканчивается созданием подстрок из непрерывных бит последовательности, пока не будет создана подстрока, которая не встречалась прежде в последовательности. Результирующая подстрока – это новое слово в словаре.
Пусть Wobs = число савокупно-определённых слов.
Например, если ε = 010110010, то просмотр происходит следующим образом:
Табл. 3.12 «Грамматический разбор» последовательности.
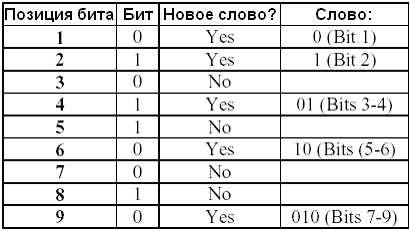
В "словаре" пять слов: 0, 1, 01, 10, 010. Следовательно, Wobs = 5.
(2) Вычисляется
P-значение =
![]() erfc
erfc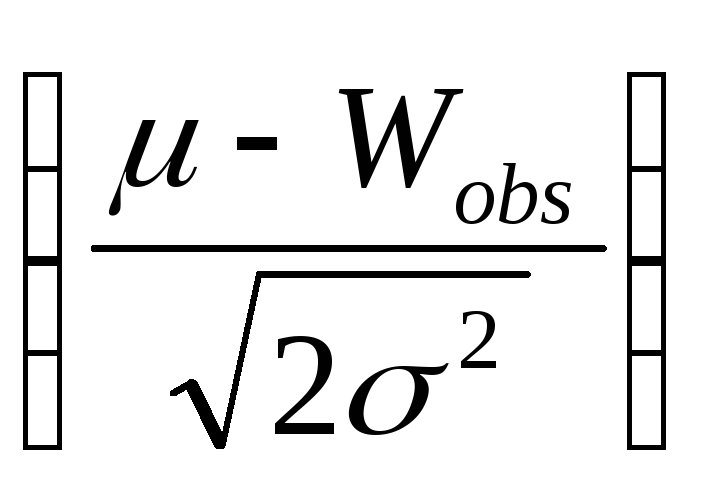 ,
где
,
где
![]() и
и![]() ,
когда
,
когда![]() .
Для других значений n,
значения
.
Для других значений n,
значения
![]() и
и
![]() должны
быть вычислены. Заметим, что т.к. нет
известной теории для определения точных
значений
должны
быть вычислены. Заметим, что т.к. нет
известной теории для определения точных
значений
![]() и
и
![]() ,
эти значения были вычислены (в предположении
случайности) с помощью генератораSHA-1.
Blum-Blum-Shub
генератор даст сходные значения для
,
эти значения были вычислены (в предположении
случайности) с помощью генератораSHA-1.
Blum-Blum-Shub
генератор даст сходные значения для
![]() и
и
![]() .
.
Т.к. длина
последовательности в нашем примере
намного меньше рекомендуемой длины,
значения для
![]() и
и![]() будут не обоснованы. Поэтому, предположим,
что тест проводится для последовательности
длиной 1000000 бит, и было получено значениеWobs
= 69600,
тогда
P-значение =
будут не обоснованы. Поэтому, предположим,
что тест проводится для последовательности
длиной 1000000 бит, и было получено значениеWobs
= 69600,
тогда
P-значение =
![]() erfc
erfc![]()
Правило принятия решения (1%- уровень)
Если вычисленное P-значение < 0.01, то считаем, что последовательность неслучайна. В противном случае, считаем, что последовательность случайна.
Выводы и интерпретация результатов.
Т.к. полученное на шаге 2 пункта 4 P-значение 0.01 (P-значение = 0.949310), делаем вывод, что последовательность случайна.
Заметим, что для
n
=
![]() ,
если бы Wobs
опустилось
ниже 69561, то мы заключили бы, что
последовательность может быть существенно
сжата и, поэтому, неслучайна.
,
если бы Wobs
опустилось
ниже 69561, то мы заключили бы, что
последовательность может быть существенно
сжата и, поэтому, неслучайна.
Рекомендации
Рекомендуется
для тестирования брать последовательности
длиной минимум
![]() бит (т.е.n≥
бит (т.е.n≥![]() ).
).
Тест линейной сложности.
Цель теста
Суть этого теста – длина сдвигового регистра с линейной обратной связью (LFSR). Цель этого теста – определить, будет или нет последовательность достаточно сложной, чтобы считаться случайной. Случайные последовательности характеризуются длинными сдвиговыми регистрами LFSR. Слишком короткий сдвиговый регистр LFSR подразумевает неслучайность.
Вызов функции
LinearComplexity(M, n), где:
M Длина блока в битах.
n Длина строки бит.
Последовательность бит, вырабатываемая генератором случайных чисел, который тестируется; = 1, 2, … , n.
K Число степеней свободы; K = 6 было принято в тестовом коде.
Тестовая статистика.
![]() :
Мера того, насколько хорошо наблюдаемое
число включений сдвиговых регистров
LFSR
фиксированной длины соответствует
числу включений в предположении
случайности.
:
Мера того, насколько хорошо наблюдаемое
число включений сдвиговых регистров
LFSR
фиксированной длины соответствует
числу включений в предположении
случайности.
Соответствующее
распределение для тестовой статистики
– это распределение
![]() .
.
Описание теста
(1) Делим n-битную последовательность на N независимых блоков из M бит, где n = MN.
(2) Используя специальный алгоритм (Berlekamp-Massey algorithm), определяем линейную сложность Li каждого из N блоков (i = 1,…,N). Li – это длина самой короткой последовательности сдвиговых регистров с линейной обратной связью, которая порождает все биты в блоке i. Внутри любой Li-битной последовательности, некоторая комбинация бит, когда складывается по модулю 2, производит следующий бит в последовательности (бит Li + 1).
Например, если M = 13 и тестируемый блок 1101011110001, то Li = 4, и последовательность порождается сложением 1-ого и 2-ого бита внутри a 4-битной подстроки чтобы получить следующий бит (5-ый бит). Процесс происходит следующим образом:
Табл. 3.13 Алгоритм определения линейной сложности
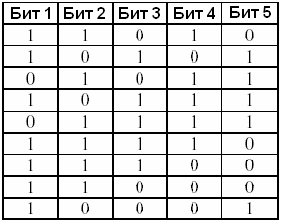
Первые 4 бита и результирующий 5-й бит:
Биты 2-5 и результирующий 6-й бит:
Биты 3-6 и результирующий 7-й бит:
.
.
.
.
.
.
Биты 9-12 и результирующий 13-й бит:
Для этого блока работает алгоритм с пробной линейной обратной связью. Могут применяться для блока и другие алгоритмы с линейной обратной связью (например, сложение бит 1-ого и 3-его для получения 5-ого бита, или сложение 1, 2 и 3-его бит для получения 6-ого бита, и.т.д.).
(3)
Предполагая случайность, вычисляем
теоретическое значение
![]() :
:
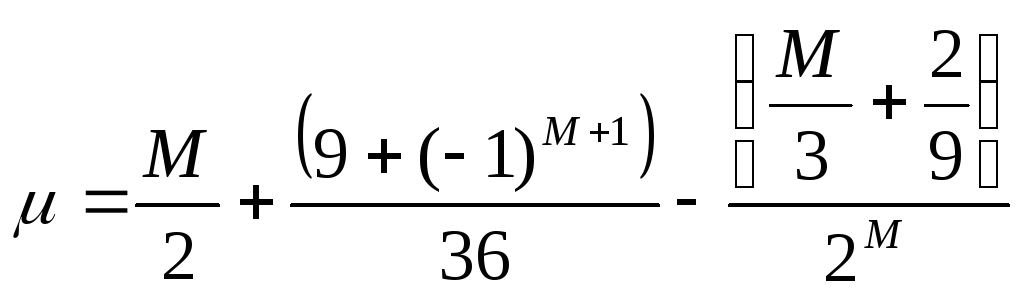 .
.
Для нашего примера,
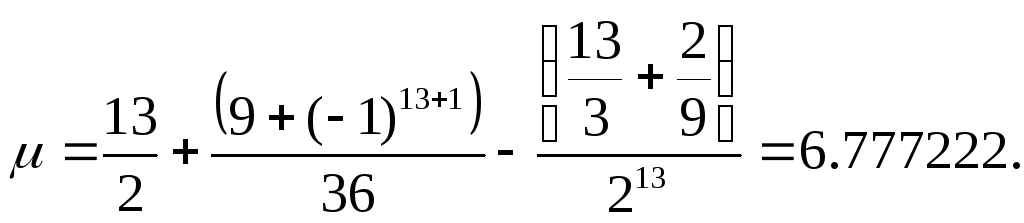
(4)
Для каждой подстроки , вычисляются
значения Ti,
где
![]() .
.
Для нашего примера,
![]() .
.
(5) Записываем значения Ti в v0,…, v6 следующим образом :
Если: Ti ≤ -2.5 Увеличиваем v0 на единицу.
-2.5 < Ti ≤ -1.5 Увеличиваем v1 на единицу.
-1.5 < Ti ≤ -0.5 Увеличиваем v2 на единицу.
-0.5 < Ti ≤ 0.5 Увеличиваем v3 на единицу.
0.5 < Ti ≤ 1.5 Увеличиваем v4 на единицу.
1.5 < Ti ≤ 2.5 Увеличиваем v5 на единицу.
Ti > 2.5 Увеличиваем v6 на единицу.
(6) Вычисляется
![]() ,
где
,
где![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
(7)
Вычисляется P-значение
= igamc![]() .
.
Правило принятия решения (1%- уровень)
Если вычисленное P-значение < 0.01, то считаем, что последовательность неслучайна. В противном случае, считаем, что последовательность случайна.
Выводы и интерпретация результатов.
Т.к вычисленное на шаге 7 пункта 4 P-значение 0.01, делаем вывод, что последовательность случайна.
Заметим, что если
бы P-значение
было <
0.01, это
указывало бы на то, что наблюдаемые
частотные отсчёты Ti
хранящиеся
в
![]() отличаются
от ожидаемых значений; предполагается,
что распределение частотыTi
(в
отличаются
от ожидаемых значений; предполагается,
что распределение частотыTi
(в
![]() )
должно быть пропорционально
)
должно быть пропорционально![]() ,
как показано на шаге 6 пункта 4.
,
как показано на шаге 6 пункта 4.
Рекомендации
Выбираем
![]() .
Значение M
должно быть
500≤
M
≤
5000, и N
≥ 200 для
получения правильного значения
.
Значение M
должно быть
500≤
M
≤
5000, и N
≥ 200 для
получения правильного значения
![]() .
.
