2. Описание параметров.

Разработанное программное обеспечение позволяет варьировать длиной блока в силу наличия такого параметра как размерность матрицы. В зависимости от размера открытого текста можно подбирать и размер матрицы, чтобы снизить число раундов маскирования.

1. Размер слова.

На данный момент разработан программный продукт, использующий алгоритм, работающий с 32-х битными словами, в дальнейшем будет разработан программный продукт, использующий алгоритм, работающий с 16-и и 64-х битными словами.

2. Размер блока.

Программный продукт, использует алгоритм, работающий с 128-ми битным блоком данных. Размер информационного массива, подлежащий маскированию, может варьироваться и быть кратным 32 бита * n, гдеn– размерность матрицы.

3. Размер ключа.

Длина ключа равна 512 бит. Ключ представляется в виде 16-ти 32-х битных блоков. Размер ключевого массива может варьироваться и быть кратным 32 бита *n², гдеn– размерность матрицы.

4. Требования, предъявляемые к ключу.

Ключ должен являться массивом статистически независимых битов, принимающих с равной вероятностью значения 0 и 1. При этом некоторые конкретные значения ключа могут оказаться «слабыми», то есть шифр может не обеспечивать заданный уровень стойкости в случае их использования. Однако, предположительно, доля таких значений в общей массе всех возможных ключей ничтожно мала. Поэтому ключи, выработанные с помощью некоторого датчика истинно случайных чисел, будут качественными с вероятностью, отличающейся от единицы на ничтожно малую величину. Если же ключи вырабатываются с помощью генератора псевдослучайных чисел, то используемый генератор должен обладать высокой криптостойкостью. Иными словами, задача определения отсутствующих членов вырабатываемой генератором последовательности элементов не должна быть проще, чем задача вскрытия алгоритма маскирования. Кроме того, для отбраковки ключей с плохими статистическими характеристиками могут быть использованы различные статистические критерии. На практике обычно хватает критерия для проверки независимости битов ключа – критерий серий.

2. Формирование ключа.

Выше были описаны требования к ключам . В соответствии с этими требованиями сформируем ключ.

В алгоритме маскирования используется 512–битный ключ. Для его формирования используем генератор псевдослучайных чисел.

С помощью генератора генерируем последовательность длиной 512 бит. Для проверки равновероятного распределения битов ключа между значениями 0 и 1 используем тест «Дырок».

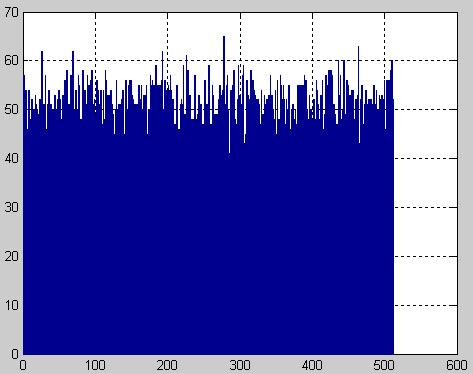
Рис. 3.2 Гистограмма последовательности

Проверим равномерность распределения 0 и 1 в исследуемой последовательности на основе анализа количества появлений «блоков» - подпоследовательностей, состоящих из одних единиц, и «дырок» - подпоследовательностей, состоящих из одних нулей.

Пусть  =  1,  2, … ,  n. – двоичная последовательность длины n = 512 бит.

Сначала определим предтестовую статистику π – долю единиц в рассматриваемой последовательности:

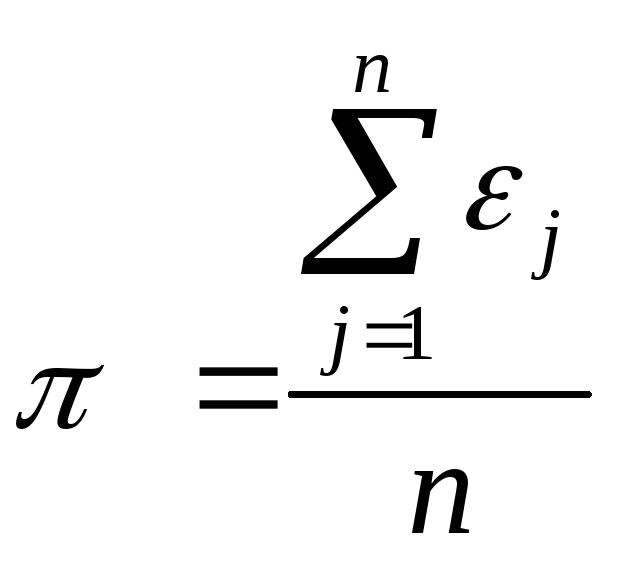
Если , то тест считается не пройденным. Для нашей последовательности π = 0,4219, т. е. 0,0781 ≤ τ = 0,088.

Вычислим статистику (количество блоков и дырок):

,

где r(k) = 0, если ε_k = ε_k+1 и r(k) = 1, если ε_k ≠ ε_k-1, и

P-значение = erfc.

Если вычисленное P-значение < 0.01, то считаем, что последовательность неслучайна. В противном случае, считаем, что последовательность случайна.

Для нашей ключевой последовательности P-значение = 0,6669.

Результатом тестирования сгенерированной последовательности по тесту «Дырок» явился результат, показывающий равномерное распределение нулей и единиц в ней.

Проверим выделенную последовательность на равновероятность распределения нулей и единиц по другому критерию. В книге Кнута «Искусство программирования» автор предлагает для коротких последовательностей использовать следующий критерий: b-ичная последовательность длины N случайна, если она k-распределена для всех положительных целых чисел .k-распределенность у Кнута вводится следующим образом. Пусть задана b-ичная последовательность X₀, X_1,…, X_N-1. Можно сказать, что , если. Такую последовательность можно назвать k-распределённой, еслидля всех b-ичных чисел x₁x₂…x_k.

Я проверил выбранный мною ключ по описанному выше критерию для k=1,2,3,4 (аналогично делается для k=5,6,7,8). Критерий дал положительный ответ, т.е. можно считать ключевую последовательность случайной и равномерно-распределённой.