
- •Пояснительная Записка
- •1 Введение 6
- •5.3 Расчет 117
- •Введение
- •Исследовательская часть
- •Структура подсистемы защиты информации в системе глобальной спутниковой связи и методы обеспечения средств мониторинга и управления объектами защиты информации
- •Описание среды комплекса спутниковой глобальной радиосвязи и выявление целей защиты информации
- •Состав и структура подсистемы защиты информации в комплексе спутниковой глобальной радиосвязи.
- •Прослушивание второго рода, как метод построения эффективных атак на систему связи.
- •Алгоритм массирования – как метод защиты от прослушивания второго рода.
- •Линейные кодовые последовательности.
- •Нелинейные кодовые последовательности.
- •Однократное гаммирование.
- •Требования к алгоритму маскирования.
- •Специальная часть
- •Основные требования.
- •Соответствие предъявляемому уровню безопастности.
- •Построение на основе использования криптографии симметричных ключей.
- •Описание.
- •Математическое описание.
- •Описание параметров.
- •Формирование ключа.
- •Разворачивание ключа.
- •Определение времени жизни сеансовых ключей
- •Программная и аппаратная гибкость реализации
- •Оценка сложности программной и аппаратной реализации
- •Вычислительная сложность (скорость) зашифрования/расшифрования
- •Оценочное время выполнения зашифрования/расшифрования блока данных
- •Оценочная скорость алгоритма в виде числа тактов работы процессора
- •Скорость выполнения зашифрования/расшифрования блока данных
- •Пакет тестов Национального института стандартов и технологий (nist)
- •Частотный тест.
- •Тест на самую длинную серию единиц в блоке.
- •Тест ранга двоичных матриц.
- •Тест с дискретным преобразованием Фурье (спектральный тест).
- •Универсальный статистический тест Маурэра.
- •Сжатие при помощи алгоритма Лемпела-Зива.
- •Тест линейной сложности.
- •Результаты тестирования
- •Результаты проведения тестов
- •Спектральный тест
- •Тест линейной сложности
- •Технологический раздел
- •Введение
- •Общие принципы тестирования
- •Общие методики оценки качества алгоритма маскирования данных
- •Графические тесты
- •Гистограмма распределения элементов
- •Распределение на плоскости
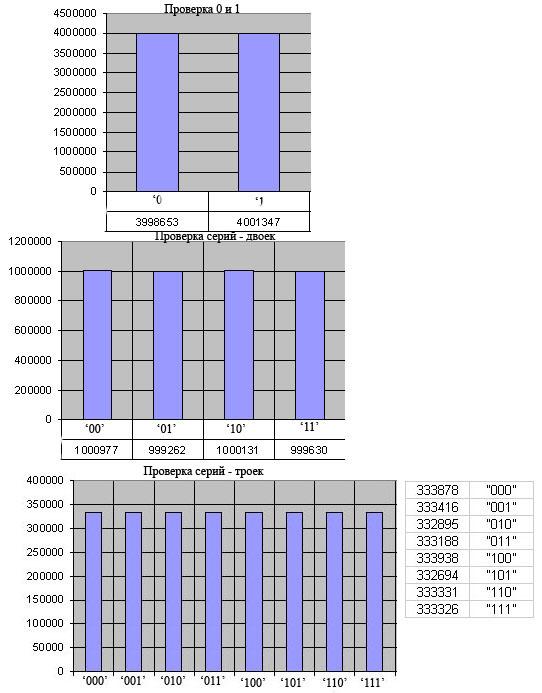
- •Проверка серий
- •Проверка на монотонность
- •Оценочные тесты
- •Методы тестирования алгоритма маскирования данных
- •Система оценки статистических свойств
- •Оценка результатов тестирования
- •Генерация последовательностей для тестирования
- •Исполнение набора статистических тестов
- •Анализ прохождения статистических тестов
- •Организационно-экономический раздел
- •Введение
- •Теоретическая часть
- •Оценка затрат на разработку по
- •Составляющие затрат на программный продукт
- •Составляющие затрат на разработку программ Ср.
- •Затраты на непосредственную разработку кп
- •Сложность комплекса программ
- •Применение современных методов разработки кп.
- •Факторы организации процесса разработки кп, влияющие на непосредственные затраты при создании сложных программ.
- •Затраты на изготовление опытного образца как продукции производственно-технического назначения.
- •Затраты на технологию и программные средства автоматизации разработки комплекса программ.
- •Составляющие затрат на эксплуатацию программ, влияющие на процесс их разработки.
- •Исходные данные
- •Расчёт затрат
- •1)Составляющие затрат на разработку программ:
- •2) Затраты на эксплуатацию программ:
- •3) Накладные расходы
- •Производственно-экологическая безопасность
- •Введение
- •Машинный зал и рабочее место программиста
- •Вредные факторы, присутствующие на рабочем месте и их классификация
- •Вредные производственные воздействия
- •Электрическая опасность
- •Нерациональность освещения
- •Расчет искусственного освещения методом коэффициента использования светового потока
- •Психофизические факторы
- •Микроклимат
- •Посторонние шумы
- •Постороннее электромагнитное излучение
- •Химические факторы
- •Эргономические требования
- •Эргономика окружающей среды
- •Экологическая безопасность
- •Заключение
- •Литература
- •Приложение 1
- •Приложение 2
- •Приложение 3
Проверка на монотонность
Данный тест позволяет оценить равномерность распределения символов в исследуемой последовательности на основе анализа длин участков невозрастания и неубывания элементов последовательности.
Построение производится следующим образом. Исследуемая последовательность ε графически представляется в виде следующих друг за другом непересекающихся участков невозрастания и неубывания элементов последовательности.
У последовательности, чьи статистические свойства близки к свойствам истинно случайной последовательности, вероятность появления участка невозрастания (неубывания) определенного размера зависит от его длины: чем больше длина, тем меньше вероятность (рис. 4.6, а). В противном случае последовательность не является случайной (рис. 4.6, б).
Пример 4.3.
Вход:
ε= 1 2 3 4 5 5 5 4 4 3 2 2 2 1 2 3 4 5.
Тест:
Разобъем последовательность на участки невозрастания и неубывания:
ε= 1234555 4432221 2345.
Получаем участок неубывания длиной 6, затем участок невозрастания длиной 7 и вновь участок неубывания длиной 4.
а

б
Рис. 4.5. Проверка серий графическая:
а – результат положительный
б – результат отрицательный

Рис. 4.6. Проверка на монотонность графическая;
а – результат положительный
б – результат отрицательный
Оценочные тесты
В отличии от графических тестов, где результаты интерпретируются пользователями, вследствие чего возможны различия в трактовке результатов, оценочные тесты характеризуются тем, что они выдают численную характеристику, которая позволяет однозначно сказать, пройден тест или нет.
В таблице 4.1 приведена информация по наиболее известным подборкам статистических тестов, применяемых для анализа криптоалгоритмов.
Таблица 4.1. Наборы статистических тестов.
|
Автор |
Где описан или где реализован |
|
Д. Кнут. (Стэнфордский Университет) |
Исскуство программирования . Том 2. Получесленные алгоритмы |
|
Дж. Марсалья |
DIEHARD |
|
Ч. Густафсон |
CRYPT-S |
|
А. Менезис |
Руководство по прикладной криптографии |
|
А. Рухин |
Руководство по статистическому тестированию генераторов ПСП |
Методы тестирования алгоритма маскирования данных
Система оценки статистических свойств
Различные статистические тесты могут применяться к программной реализации алгоритма маскирования информационных данных, для того чтобы сравнить выходные данные с истинно случайной последовательностью. Случайность – вероятностное свойство; это означает, что свойства случайной последовательности могут быть охарактеризованы и описаны в терминах вероятности. Вероятный результат статистических тестов, применяемых к истинно случайной последовательности, известен априорно и может быть описан в вероятностных терминах. Существует много статистических тестов, оценивающих присутствие или отсутствие «образца», который при обнаружении указал бы, что последовательность неслучайна. Поскольку существует так много тестов, оценивающих, является ли последовательность случайной или нет, никакой определенный конечный набор тестов не считают «законченным». Кроме этого, результаты статистического теста должны интерпретироваться с некоторой осторожностью и предостережением, чтобы избежать неправильных заключений.
Каждый тест основан на вычислении значения тестовой статистики, которое является функцией данных. Если значение тестовой статистики есть S, аt– критическое значение (теоретическое эталонное распределение для этой статистики), то вероятность ошибки 1-ого рода и 2-ого рода есть соответственно
P( S > t || H0 истина) = Р(отклонить H0 | H0 истина),
P( S ≤ t || H0 ложна) = Р(принять H0 | H0 ложна),
Тестовая статистика использует вычисление Р-значение, гдеР-значениеесть вероятность того, что совершенный генератор случайных чисел произвел бы последовательность менее случайную, чем исследуемая, для типа неслучайности, проверяемого тестом. ЕслиР-значениедля теста равно 1, то последовательность абсолютно случайна.Р-значение, равное 0, указывает, что последовательность абсолютно неслучайна. Для теста следует выбрать уровень значимости α. ЕслиР-значениебольше или равно α, то принимается нулевая гипотеза (H0– гипотеза о том, что проверяемая последовательность является случайной), т.е. последовательность кажется случайной. ЕслиР-значение меньше α, то нулевая гипотеза отклоняется, т.е. последовательность кажется неслучайной. Параметр α обозначает вероятность ошибки 1-ого рода.
Значение α, равное 0.01, говорит о том, что из 100 случайных последовательностей не прошла бы тест только одна. При Р-значении≥ 0.01 последовательность рассматривается как случайная с доверительностью 99%. ПриР-значении< 0.01 последовательность рассматривается как неслучайная с доверительностью 99%.
По отношению к исследуемым выходным данным программного обеспечения маскирования данных можно сделать следующие предположения.
Равномерность. В любой точке при формировании выходной последовательности случайных или псевдослучайных битов 0 и 1 равновероятны и вероятности их появления равны ½. Ожидаемое число нулей (или единиц) равно n/2, гдеn– длина последовательности.
Масштабируемость. Любой тест, применяемый к выходной последовательности, может также применяться к произвольной подпоследовательности. Если последовательность случайна, то любая ее подпоследовательность должна также быть случайна. Следовательно, любая подпоследовательность должна пройти все тесты на случайность.
В таблице 4.2 даны общие характеристики статистических тестов.
Таблица 4.2. Набор статистических тестов.
|
№ |
Статистический тест |
Определяемый дефект |
|
1. |
Частотный тест |
Слишком много нулей или единиц |
|
2. |
Проверка кумулятивных сумм |
Слишком много нулей или единиц в начале последовательностей |
|
3. |
Проверка «дырок» в подпоследовательностях |
Отклонение в распределении подпоследовательностей единиц |
|
4. |
Проверка «дырок» |
Большое (малое) число подпоследовательностей нулей и единиц свидетельствуют, что колебание потока бит слишком быстрое (медленное) |
|
5. |
Проверка рангов матриц |
Отклонение распределения рангов матриц от соответствующего распределения для истинно случайной последовательности, связанное с периодичностью подпоследовательностей |
|
6. |
Спектральный тест |
Периодические свойства последовательностей |
|
7. |
Проверка непересекающихся шаблонов |
Непериодические шаблоны встречаются слишком часто |
|
8. |
Проверка пересекающихся шаблонов |
Слишком часто встречаются m-битные последовательности единиц |
|
9. |
Универсальный статистический тест Маурера |
Сжимаемость (регулярность) последовательности |
|
10. |
Проверка случайных отклонений |
Отклонение от распределения числа появлений подпоследовательностей определенного вида |
|
11. |
Разновидность проверки случайных отклонений |
Отклонение от распределения числа появлений подпоследовательностей определенного вида |
|
12. |
Проверка аппроксимированной энтропии |
Неравномерность распределения m –битных слов. Малые значения означают высокую повторяемость |
|
13 |
Проверка серий |
Неравномерность распределения m-битных слов |
|
14. |
Сжатие при помощи алгоритма Лемпела –Зива |
Большая сжимаемость, чем истинно случайная последовательность |
|
15. |
Линейная сложность |
Отклонение то распределения линейной сложности для конечной длины (под) строки |
Итак, оценка статистических испытаний основана на проверке гипотезы о случайности исследуемой последовательности нулей и единиц. Таблица 4.3. показывает пошаговый процесс, позволяющий оценить конкретную двоичную последовательность.
Таблица 4.3. Процедура оценки
|
Номер шага |
Пошаговый процесс |
Комментарии |
|
1. |
Постановка гипотезы |
Предполагаем, что последовательность является случайной |
|
2. |
Вычисление тестовой статистики последовательности |
Проводим тестирование на битовом уровне |
|
3. |
Вычисляем Р -значение |
Р
–значение |
|
4. |
Сравнение
Р –значения
с |
Задаем Если
Р –значение> |
