1. Линейные кодовые последовательности.

Типичными и наиболее распространенными являются М-последовательности (рис. 2.3.), для которых справедливо рекуррентное правило:

, (2.1)

где – характеристический многочлен. Комбинация символов 00..000 является запрещенной, поскольку все последующие вычисления по выражению (2.1) приведут к нулевому результату.

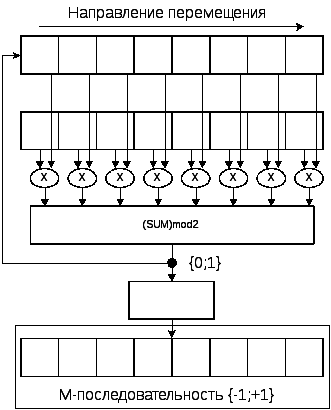
Рис. 2.3. Схема формирования М-последовательности

На основании полученной последовательности символов формируется расширяющая функция. Таким образом, при длинехарактеристического многочлена период формируемой последовательности не может превышатьсимволов. Период М-последовательности. Ширина спектра М-последовательности определяется ее самым коротким элементом – символом и равна, в то время как база такого сигнала –.

Важными характеристиками М-последовательности являются свойства ее автокорреляционной функции (АКФ). Для ее построения используется математическая операция свертка. Свертка вычисляется как в частотной, так и во временной областях.

Схема вычисления свертки во временной области приведена на рис. 2.4. Если длины сворачиваемых последовательностей PиQравныLPиLQ, то длина свертки равнаLP+LQ–1.

АКФ формируется с помощью свертки М-последовательности самой на себя.

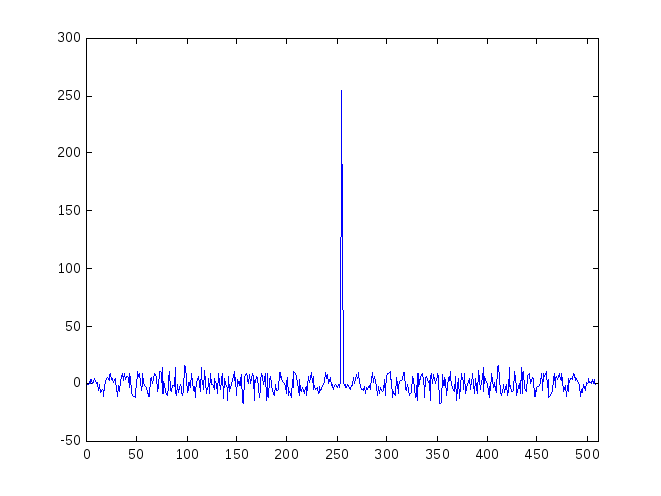
В качестве основных свойств АКФ являются величина пика и максимальный уровень боковых лепестков. На практике применяются М-последовательности, указанные величины АКФ для которых равны исоответственно (рис. 2.5.).

Для выявления М-последовательностей при заданном значении mосуществляется перебор всевозможных вариантов характеристического многочлена С = 000…00 – 111…11. Дляm=8 их число равно 256, однако не при всех С будет сформирована М-последовательность.

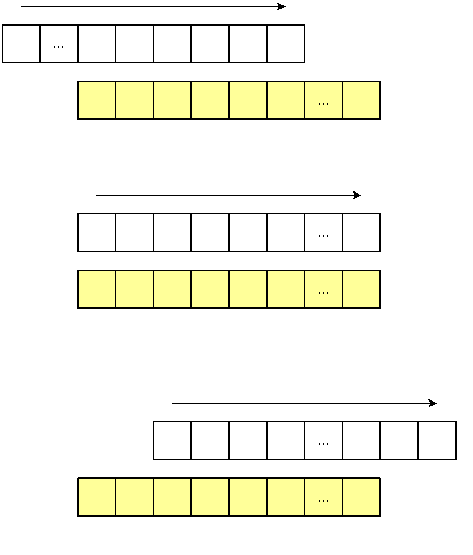
Рис. 2.4. Схема вычисления свертки (затемненная последовательность неподвижна)

Пик

Рис. 2.5. Типичные вид и свойства АКФ для М-последовательности

Для передачив эфир каждый бит информации (“1” либо “0”) кодируется последовательностьюлибо. Допустим, что в эфир передается (11 бит), используетсяM-последовательность длиной 255 символов. Тогда длина выдаваемой в эфир последовательности равна 11 х 255  = 2805 символов.

Для моделирования обработки сигнала в приемном устройстве необходимо свернуть последовательность (из 2805 символов для рассматриваемого примера) с последовательностью (из 255 символов для рассматриваемого примера). На рис. 2.6. положительный пик соответствует принятому биту «1» и отрицательный пик – биту «0».

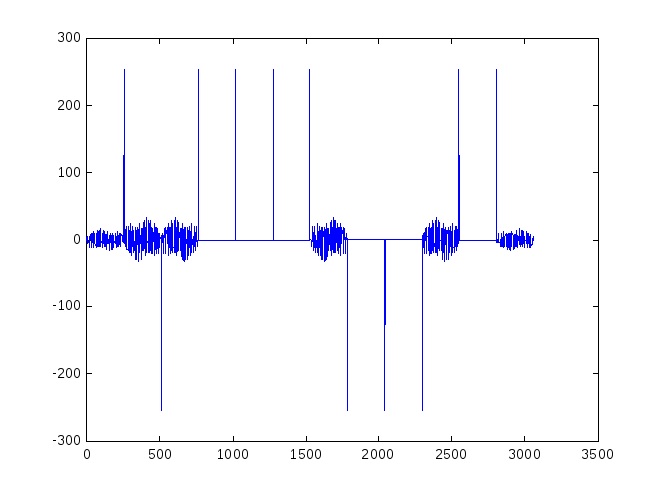
Рис. 2.6. Типичный вид принятого сигнала после свертки

При относительной простоте генерации линейные рекуррентные кодовые последовательности имеют низкую структурную скрытность. В соответствии с соотношением (2.1) для формирования М-последовательности нужно знать коэффициентов. Их можно определить изуравнений вида (2.1) относительно неизвестныхи.

2. Нелинейные кодовые последовательности.

Лучшей структурной скрытностью обладают нелинейные кодовые последовательности:

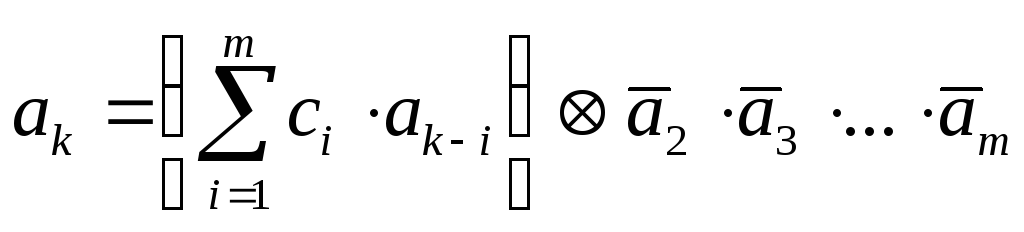, (2.2)

Наличие дополнительного члена, образующего нелинейную обратную связь, позволяет исключить зацикливание в связи с выработкой комбинации 00...000.

Схема формирования последовательности согласно выражению (2.2) приведена на рис. 2.6.

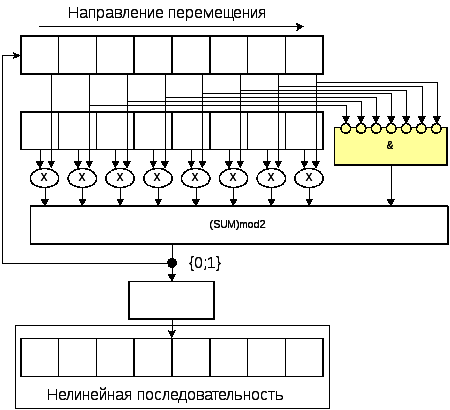
Рис. 2.6. Схема формирования нелинейной последовательности

Для зондирования местности и объектов с целью восприятия в радиолокационном диапазоне волн применяют внутриимпульсную модуляцию. Одним их распространенных способов является линейно-частотное модулирование (ЛЧМ).

При этом комплексный сигнал

, (2.3)

где a(t)=1,f₀=0,T=1,t= -0.5:0.001:0.5 после излучения также подвергается операции свертки (сжатию) в приемном тракте. Действительная и мнимая составляющие ЛЧМ-сигнала приведены на рис. 2.7.

Для свертки (обозначение: * ) комплексных сигналов во временной области необходимо вычислить 4 свертки действительных сигналов. Пусть – принимаемый сигнал,– сигнал в приемнике. Тогда:

. (2.4)

Для сигнала :re=real( u(t) ),im= –imag( u(t) ), для сигнала:re=real( u(t) ),im=imag( u(t) ). Различие заключается в знаке перед мнимыми частями.

В качестве примера на рис. 2.8. приведен результат свертки ЛЧМ-сигнала. Отчетливо виден пик, по которому обнаруживается принятый ЛЧМ-сигнал.

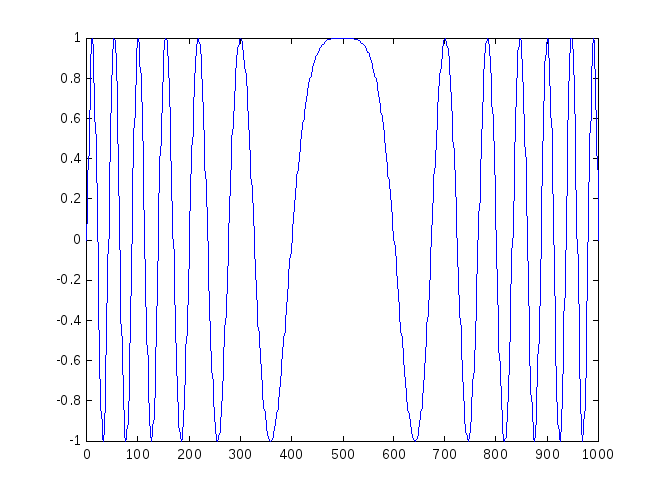
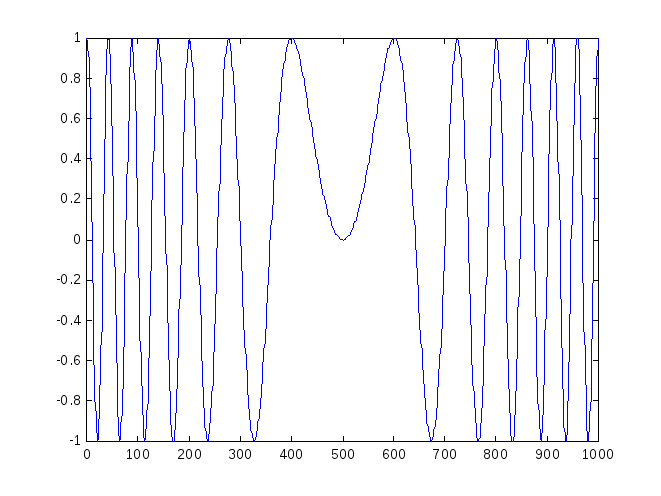
Рис. 2.7. Комплексные (Re, Im) составляющие ЛЧМ-сигнала

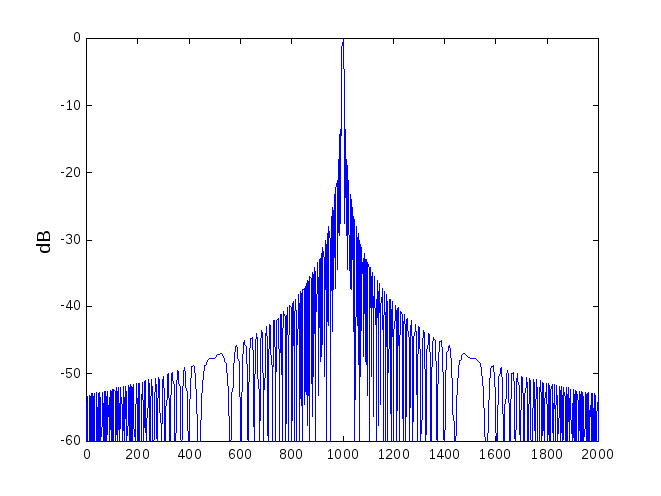
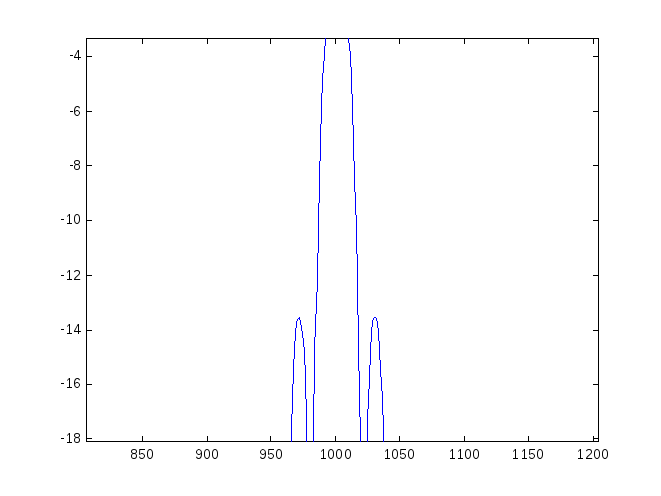
Рис. 2.8. Вид ЛЧМ- сигнала после свертки (сжатия)

При относительной простоте генерации нелинейные рекуррентные кодовые последовательности имеют также малую структурную скрытность и как линейные рекуррентные кодовые последовательности обладают большим коэффициентом избыточности.