1. Графические тесты

К данной категории можно отнести, например, следующие тесты:

• гистограмма распределения элементов последовательности;

• распределение на плоскости;

• проверка серий;

• проверка на монотонность;

• автокорреляционная функция;

• профиль линейной сложности;

• графический спектральный тест.

1. Гистограмма распределения элементов

Данный тест позволяет оценить равномерность распределения символов в исследуемой последовательности, а также определить частоту появления конкретного символа.

Строится гистограмма следующим образом. В исследуемой последовательности ε подсчитывается, сколько раз встречается каждый элемент, после чего строится график зависимости числа появлений элементов от их численного представления (ASCII-значение для байтов).

Пример 4.1

Вход:

ε = 0 1 2 1 3 2 1

Тест:

Преобразуем исходную последовательность байтов в последовательность ASCII – значений символов:

ε = 48 49 50 49 51 50 49;

теперь подсчитаем, сколько раз встречается каждое значение:

n₄₈ = 1,

n₄₉ = 3,

n₅₀ = 2,

n₅₁ = 1.

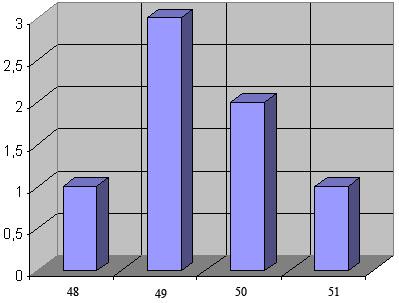
Для того чтобы последовательность удовлетворяла свойствам случайности, необходимо, чтобы в ней присутствовали все возможные элементы рассматриваемой разрядности, при этом разброс частот появления символов стремиться к нулю (рис 4.1, а). В противном случае последовательность не является случайной (рис 4.1, б).

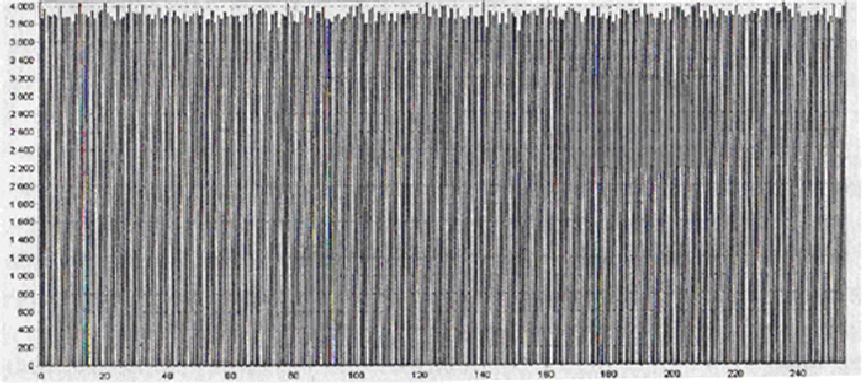а

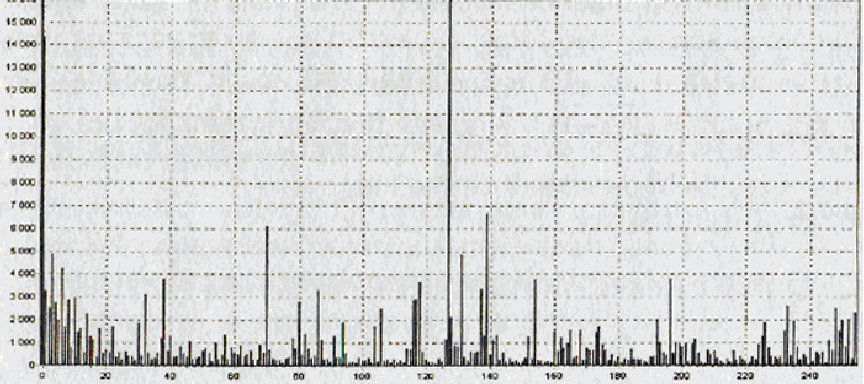б

Рис. 4.1. Примеры гистограмм:

а – результат положительный;

б – результат отрицательный;

Данный тест может принести пользу также в тех случаях, когда оценивается качество последовательности с законом распределения, отличным от равномерного, либо последовательности, в которой некоторые символы вообще отсутствуют (рис. 4.2).

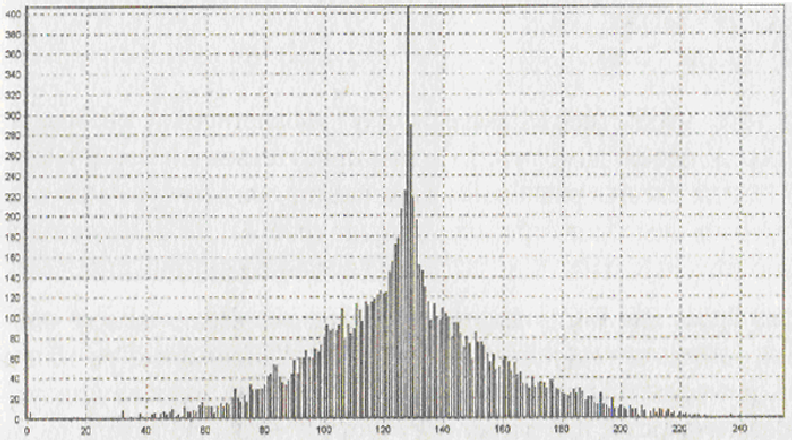Рис. 4.2. Пример гистограммы последовательности с законом распределения символов, близким к нормальному

2. Распределение на плоскости

Данный тест предназначен для определения зависимостей между элементами исследуемой последовательности.

Построение распределения на плоскости осуществляется следующим образом. На поле размером (2^r - 1) * (2^r - 1) (R – разрядность чисел исследуемой последовательности) наносятся точки с координатами (ε_i; ε_i+1), где ε_i- элементы исследуемой последовательности ε, i = 1, (n-1), n – длина последовательности.

Пример 4.2

Вход:

ε = 2 3 5 4 3.

Тест:

Получаем точки:

точка 1 (2;3),

точка 2 (3;5),

точка 3 (5;4),

точка 4 (4;3).

Далее анализируется полученная картина. Если между элементами последовательности отсутствуют зависимости, то точки на поле расположены хаотично (рис. 4.3, а). Если на поле присутствуют зависимости, наблюдаются «узоры» - последовательность не является случайной (рис. 4.3, б). Для последовательностей большой длины хорошим результатом является абсолютно черное поле (рис. 4.4).

Рис. 4.3. Распределение на плоскости:

а – результат положительный

б – результат отрицательный

Рис. 4.4 Распределение на плоскости (положительный результат для последовательности большой длины)

3. Проверка серий

Данный тест позволяет оценить равномерность распределения символов в исследуемой последовательности на основе анализа частоты появления нулей и единиц и серий, состоящих из k бит.

Построение осуществляется следующим образом. Подсчитывается, сколько раз встречаются нули, единицы, серии-двойки (00, 01, 10, 11), серии-тройки (000, 001, 010, 011, 100, 101, 110, 111) и т. д. в битовом представлении исследуемой последовательности ε. Полученные результаты представляются в графическом виде.

Пример 4.3.

Вход:

ε= 2 6 4 7 1 8 3.

Тест:

Представляем исходную последовательность в битовом виде:

ε=0010 0110 0100 0111 0001 1000 0011;

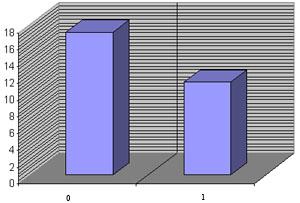
подсчитываем число единиц и нулей:

ε=0010011001000111000110000011;

n ₀ = 17,

n ₁ = 11;

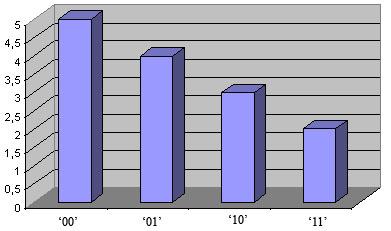
Подсчитываем число серий – пар каждого вида:

ε=00 10 01 10 01 00 01 11 00 01 10 00 00 11;

n ₀₀ = 5,

n ₀₁ = 4,

n ₁₀ = 3,

n ₁₁ = 2;

Подсчитываем число серий – троек каждого вида (последний бит отбрасывается, так как он не входит в состав тройки):

ε=001 001 100 100 011 100 011 000 001 1;

n ₀₀₀ = 1,

n ₀₀₁ = 3,

n ₀₁₀ = 0,

n ₀₁₁ = 2;

n ₁₀₀ = 3,

n ₁₀₁ = 0,

n ₁₁₀ = 0,

n ₁₁₁ = 0.

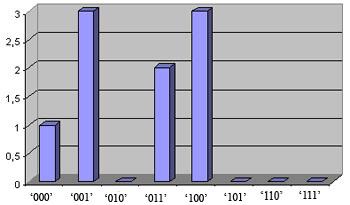
У последовательности, чьи статистические свойства близки к свойствам истинно случайной последовательности, разбросы меж­ду числом появлений нулей и единиц, между числом появлений серий-пар каждого вида и между числом появлений серий-троек каждого вида должны стремиться к нулю (рис. 4.5, а). В противном случае последовательность не является случайной (рис. 4.5, б).