3. Тест ранга двоичных матриц.

1. Цель теста

Суть теста – ранг отдельных подматриц всей последовательности. Цель этого теста – проверить на линейность зависимость среди подстрок постоянной длины исходной последовательности. Заметим, что этот тест также присутствует в серии тестов DIEHARD.

2. Вызов функции

Rank(n), где:

n Длина строки бит.

 Последовательность бит, вырабатываемая генератором случайных чисел, который тестируется;  =  1,  2, … ,  n.

M Число строк в каждой матрице. Для ряда тестов, M устанавливается равной 32. Если используются другие значения M, необходимо вычислять новые приближения.

Q Число столбцов в каждой матрице. Для ряда тестов, Q устанавливается равной 32. Если используются другие значения Q, необходимо вычислять новые приближения.

3. Тестовая статистика.

: Мера того, насколько хорошо исследуемое число рангов различных порядков соответствует ожидаемому числу рангов случайной последовательности.

Соответствующее распределение для тестовой статистики – это распределение .

4. Описание теста

(1) Последовательно делим последовательность на MQ-битные отдельные блоки; будет таких блоков. Отброшенные биты в дальнейших вычислениях не используются. ПредставляемMQ-битные сегменты в виде матриц M Q.

Каждая строка матрицы заполнена Q-битными блоками исходной последовательности ε.

Например, если n = 20, M = Q = 3, и ε = 01011001001010101101, то делим поток на N = матрицы размерностью MQ (33 = 9). Заметим, что последние два бита последовательности (0 и 1) отбрасываются. Получившиеся матрицы : 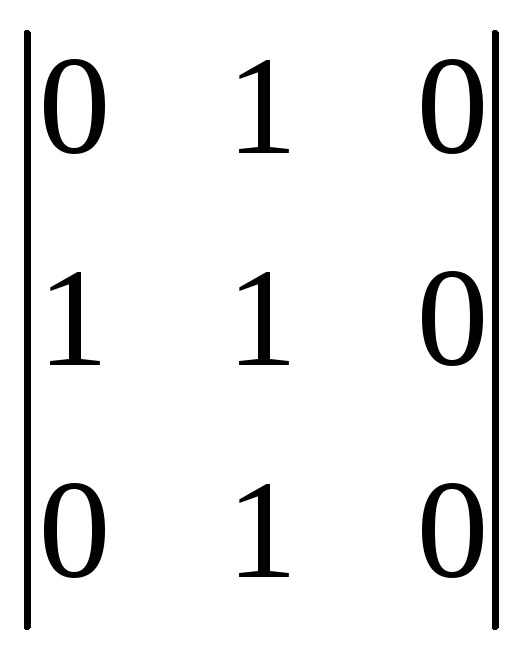и.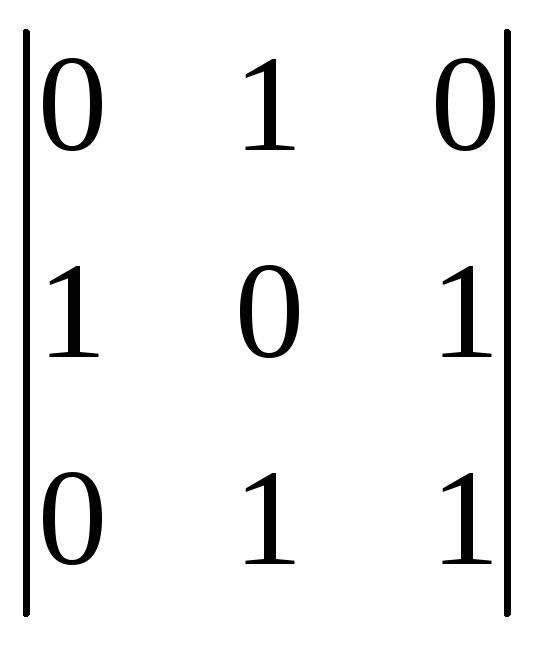

(2) Определяем двоичный ранг каждой матрицы, гдеl=1,…,N. Метод определения ранга описан в приложении А.

Для нашего примера, ранг первой матрицы равен 2 (R1 = 2), ранг второй матрицы равен 3 (R2 = 3).

(3) Обозначим FM = число матриц с рангом = M (max ранг),

FM-1 = число матриц с рангом = M-1 (max ранг - 1),

N – FM - FM-1 = число оставшихся матриц.

Для нашего примера, FM = F3 = 1 (R2 имеет max ранг 3), FM-1 = F2 = 1 (R1

имеет ранг 2), и нет матриц, имеющих любой меньший ранг.

(4) Вычисляется

.

Для нашего примера,

(5) Вычисляем Р-значение = . Т.к. в примере 3 класса, P-значение для примера равно igamc.

Для нашего примера, Р-значение = .

5. Правило принятия решения (1%- уровень)

Если вычисленное P-значение < 0.01, то считаем, что последовательность неслучайна. В противном случае, считаем, что последовательность случайна.

6. Выводы и интерпретация результатов.

Т.к. вычисленное на шаге 5 пункта 4 P-значение 0.01 (P-значениеe = 0.741948), делаем вывод, что последовательность случайна.

Заметим, что большие значения (и, следовательно, маленькие P-значения) указывают на отклонение распределения ранга от распределения ранга в случайной последовательности.

7. Рекомендации

Вероятности для M = Q = 32 были вычислены и введены в тесте. Могут быть выбраны и другие значения для M и Q, но необходимо будет вычислить новые вероятности. Минимальное число бит в тестируемой последовательности должно быть n ≥38MQ (т.е., должно быть по крайней мере 38 матриц). Для M = Q = 32, каждая тестируемая последовательность должна состоять минимум из 38912 бит.