1. Частотный тест.

1. Цель теста

Суть теста – количественное соотношение нулей и единиц во всей последовательности. Цель этого теста – определить, будет ли число единиц и нулей в последовательности приблизительно таким же, как в случайной последовательности. Тест оценивает близость количества единиц к ½ длины всей последовательности, то есть число нулей и единиц в последовательности должно быть примерно одинаковым. Все последующие тесты зависят от прохождения этого теста; нет признака, указывающего на то, что протестированная последовательность неслучайна.

2. Вызов функции

Frequency(n), где:

n Длина строки бит.

 Последовательность бит, вырабатываемая генератором случайных чисел, который тестируется;  =  1,  2, … ,  n.

3. Тестовая статистика и распределение.

S_obs: Абсолютное значение суммы Xi (где, Xi = 2 - 1 = 1) в последовательности делится квадратным корнем длины последовательности.

Соответствующее распределение для тестовой статистики полунормальное (для больших n). ( Если z (где z ) распределена нормально, то |z| распределена полунормально.)

Если последовательность случайна, то единицы с плюсами и минусами сократятся, и статистика будет близка к 0. Если же в последовательности много нулей или единиц, то тестовая статистика будет сильно отличаться от нуля.

4. Описание теста

(1) Замена 0-й и 1-ц на 1: Нули и единицы входной последовательности () заменяются на значения –1 и +1 и суммируются , где Xi = 2i –1.

Например, если  = 1011010101, то n=10 и Sn = 1 + (-1) + 1 + 1 + (-1) + 1 + (-1)

+ 1 + (-1) + 1 = 2.

(2) Вычисляется статистика

Для нашего примера

(3) Вычисляется P-значение =erfc, где erfc – комплементарная функция ошибок.

Для нашего примера P-значение =erfc= 0.527089.

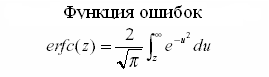
5. Правило принятия решения (1%- уровень)

Если вычисленное P-значение < 0.01, то считаем, что последовательность неслучайна. В противном случае считаем, что последовательность случайна.

6. Выводы и интерпретация результатов.

Так как полученное на 3-м шаге пункта 4 Р-значение ≥0,01 (Для нашего примера P-значение = 0.527089), то заключаем, что последовательность случайна.

Если бы Р-значение было мало(< 0.01), то соответственно было бы велико значение или. Большие положительные значенияS_n указывают на большое количество единиц в последовательности, и большие отрицательные значения S_n указывают на большое количество нулей.

7. Рекомендации

Рекомендуется для тестирования брать последовательности, длина которых ≥100 бит.

n≥100.

2. Тест на самую длинную серию единиц в блоке.

1. Цель теста

Суть этого теста – самая длинная серия единиц внутри М-битного блока. Цель этого теста – определить, будет ли длина самой длинной серии единиц внутри тестируемой последовательности близка к длине самой длинной серии единиц, которая бы ожидалась в случайной последовательности. Заметим, что неправильность ожидаемой длины самой длинной серии единиц предполагает неправильность ожидаемой длины самой длинной серии нулей. Поэтому, достаточно провести только тест для единиц.

2. Вызов функции

LongestRunOfOnes(n), где:

n Длина строки бит.

• Последовательность бит, вырабатываемая генератором случайных чисел, который тестируется;  =  1,  2, … ,  n.

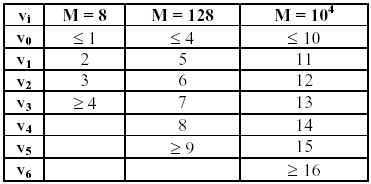
M Длина каждого блока. В зависимости от длины тестируемой последовательности выбирается одно из трёх значений M: M = 8, M = 128 и M = 10⁴ в соответствии с таблицей 3.4.

Табл. 3.4 Выбор значения M

N Число блоков; выбирается в соответствии со значением М.

3. Тестовая статистика.

: Мера того, насколько хорошо длина самой большой серии внутри M-битных блоков соответствует ожидаемой длине самой большой серии внутри М-битных блоков случайной последовательности.

Соответствующее распределение для тестовой статистики – это распределение .

4. Описание теста

(1) Делим последовательность на M-битные блоки.

(2) Располагаем в виде таблицы частоты самых длинных серий единиц в каждом блоке по категориям, где каждая ячейка содержит число серий единиц данной длины (табл. 3.5).

Для возможных значений M, ячейки v_i будут содержать следующие значения:

Табл. 3.5 Частоты самых длинных серий единиц в каждом блоке.

(3) Вычисляем , где значения 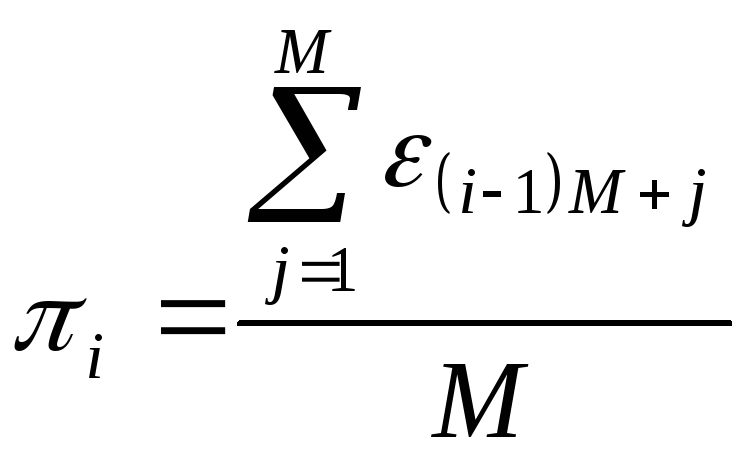, для 1i N.

Значения K и N определяются значением M в соответствии с таблицей 3.6.

Табл. 3.6 Определение значенийK и N.

(4) Вычисляется P-значение = igamc, где igamc - это неполная гамма-функция для Q(a,x) .

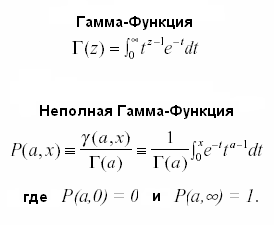
5. Правило принятия решения (1%- уровень)

Если вычисленное P-значение < 0.01, то считаем, что последовательность неслучайна. В противном случае, считаем, что последовательность случайна.

6. Выводы и интерпретация результатов.

Заметим, что большие значения указывают на то, что тестируемая последовательность содержит группы единиц.

7. Рекомендации

Рекомендуется для тестирования брать последовательности, состоящие минимум из количества бит, указанного в таблице пункта 2.