Пусть функция f(x) задана на некотором промежутке вида (a; +1). Прямую y = kx + b называют асимптотой (наклонной при k 6= 0 и горизонтальной при k = 0) функции f при x ! +1, если

lim f(x) (kx + b) = 0:

x!+1

Чтобы найти асимптоты, сначала выясняют, существует ли предел

f(xx):

Если этот предел существует и равен k, то рассматривают вопрос о существовании предела

lim (f(x) kx)

x!+1

и, если он существует и равен b, то прямая y = kx + b является асимптотой.

Аналогично определяют и находят асимптоты при x ! 1. Рассматриваются также вертикальные асимптоты: если для конечного a существует бесконечный предел limx!a+0 f(x) или limx!a 0 f(x), то прямую x = a называют вертикальной асимп-

тотой.

Например, прямые x = =2 + k , k 2 Z, являются вертикальными асимптотами функции y = tg x.

§ 6.8. Некоторые классические неравенства

Теорема 6.8.1 (Неравенство Янга). Пусть p > 1 и q – сопряжённое с p число, т. е.

Тогда для любых неотрицательных чисел x и y справедливо неравенство

называемое неравенством Янга.

Доказательство. Достаточно рассмотреть только положительные x и y.

считая y фиксированным положительным параметром, и покажем, что ' принимает только неотрицательные значения. Это и будет означать справедливость неравенства Янга.

По знаку первой производной

d'(x) = xp 1 y dx

находим, что функция '(x) строго убывает при x 6 y1=(p 1), а при x > y1=(p 1) строго возрастает. Значит, минимальное значение '(x) имеет при x = y1=(p 1).

Так как q = p=(p 1), то при всех x > 0

'(x) > ' y1=(p 1) = p1yp=(p 1) + 1q yq y1=(p 1)+1 = 0:

Теорема доказана.

Функция ' обращается в нуль только при x = y1=(p 1), т. е. когда xp = yq. Поэтому знак равенства в (6.8.2) имеет место в том и только том случае, когда xp = yq.

Отметим, что число, сопряжённое с p, часто обозначают p0.

Теорема 6.8.2 (Неравенство Гёльдера). Пусть p > 1 и q –

сопряжённое с p число. Тогда для любых двух наборов по n неотрицательных чисел a1; : : : ; an и b1; : : : ; bn справедливо неравенство

называемое неравенством Гёльдера.

Доказательство. Достаточно рассмотреть случай, когда и среди ak и среди bk есть числа, отличные от нуля.

Для каждого k = 1; : : : ; n положим

Доказательство. Достаточно рассмотреть случай, когда сумма в левой части (6.8.5) положительна. Запишем тождество

и к каждой из сумм в его правой части применим неравенство Гёльдера:

приходим к (6.8.5). Теорема доказана.

Отметим частный случай неравенства (6.8.5), когда p = 2:

Если при n = 3 тройки чисел (a1; a2; a3) и (b1; b2; b3) считать компонентами векторов в ортонормированном базисе, то неравенство Коши–Буняковского даст оценку модуля скалярного произведения векторов через длины этих векторов. А неравенство (6.8.6) даст оценку длины суммы векторов через длины этих векторов. Поэтому неравенство (6.8.6), как и неравенство Минковского (6.8.5), называют также неравенством треугольника.

Теорема 6.8.5 (Неравенство Иенсена). Пусть функция f(x)

выпукла на промежутке [a; b]. Тогда для любых n точек x1;

называемое неравенством Иенсена.

Доказательство. Положим

n

X

s := kxk:

k=1

Тогда s 2 (a; b). Пусть

y= L(x s) + f(s)

–опорная прямая функции f(x) в точке s. При всех x 2 [a; b] имеем

В частности, для каждого k = 1; : : : ; n

f(xk) > L(xk s) + f(s):

Умножим эти оценки на k и сложим полученные неравенства по k от 1 до n:

Отсюда вытекает (6.8.7). Теорема доказана.

Если функция f строго выпукла, то неравенство (6.8.8) при x 6= s является строгим. Значит, в этом случае строгим является и неравенство (6.8.7).

Если функция f(x) вогнута на промежутке [a; b], то при тех же условиях на точки xk и числа k неравенство Иенсена имеет вид

XX

Сравним с помощью неравенства Иенсена среднее арифметическое и среднее геометрического произвольного набора положительных чисел. При этом будет использована вогнутость функ-

ции ln x, в которой легко убедиться по знаку второй производной:

(ln x)00 = 1=x2 < 0.

Пусть x1; x2; : : : ; xn – произвольные числа. Средним арифметическим этих чисел называется выражение

1

n (x1 + x2 + + xn);

а средним геометрическим, если эти числа положительны, – выражение

Поэтому в силу возрастания показательной функции ex

Таким образом, установлено следующее утверждение.

Теорема 6.8.6. Для любых положительных чисел x1; : : : ; xn справедливо неравенство

т. е. среднее геометрическое положительных чисел не превосходит их среднего арифметического.

Формула (6.8.10) при n = 2

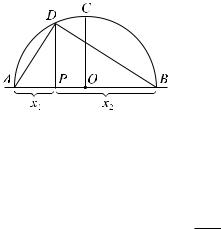
допускает простую геометрическую интерпретацию. Построим на отрезке AB длины x1 + x2 как на диаметре полуокружность, обозначим её центр O.

Пусть радиус OC ? AB, длина OC равна (x1 + x2)=2. Если DP ? AB, то из подобия прямоугольных треугольников M ADP и M DBP следует, что длина отрезка DP равна px1x2.

Таким образом, неравенство (6.8.11) означает, что длина перпендикуляра, опущенного из произвольной точки рассматриваемой полуокружности на диаметр AB, не превосходит длины радиуса OC.

Теорема 6.8.7 (Неравенство Чебышева). Если числа a1; : : :

которое называют неравенством Чебышева.

Доказательство. Имеем

X X X X

Если в полученной двойной сумме поменять индексы k и m, значение суммы не изменится. Значит,

nn

В силу (6.8.12) для любых индексов k и m имеем (ak am) (bk bm) > 0. Поэтому (6.8.13) вытекает из (6.8.14).

Легко убедиться, что если одна из последовательностей a1; : : : , an и b1; : : : ; bn возрастает, а другая убывает, то в (6.8.13) нужно заменить знак неравенства 6 на >.

Если все числа bk равны между собой, то при любых ak в (6.8.13) имеет место знак равенства. Это показывает, в частности, что множитель n в правой части неравенства (6.8.13) нельзя заменить на меньший.

Установленные в этом параграфе неравенства можно значительно обобщить. С некоторыми такими обобщениями мы познакомимся в дальнейшем.