Показательную функцию, у которой в качестве основания взято число e, называют экспоненциальной. Вместо ex пишут также exp x. Это обозначение удобно, например, когда x является дробью.

§ 4.7. Элементарные функции

Логарифмическая функция. Показательная функция y = ax, где a > 0 и a 6= 1, строго монотонна и непрерывна на всей оси, а область её значений – полуось (0; +1). Поэтому на (0; +1) существует обратная функция, которую называют логарифмической функцией по основанию a и обозначают x = loga y.

Далее независимую переменную будем, как обычно, обозначать x, а зависимую y, т. е. будем говорить о функции y = loga x.

Учитывая характер монотонности функции ax, видим, что при a > 1 функция loga x строго возрастает от 1 до +1, а при 0 < a < 1 строго убывает от +1 до 1. График логарифмической функции имеет вид:

y

a>1

110 Гл. 4. Непрерывные функции

Поскольку показательная и логарифмическая функции являются взаимно обратными, справедливы тождества

aloga x = x; x > 0; loga ax = x; x 2 R:

Выведем с помощью этих тождеств свойства логарифмов.

10: loga(xy) = loga x + loga y для любых положительных чисел

xи y.

Всамом деле,

aloga(xy) = x y = aloga xaloga y = aloga x+loga y:

Так как показательная функция принимает каждое свое значение только один раз, то в полученном равенстве можно приравнять показатели степени, что приводит к требуемому результату.

20: Из 10 для положительных x и y получаем

Таким образом, для любых положительных чисел x и y

loga xy = loga x loga y:

30: Если x > 0, то при каждом y справедливо равенство

loga xy = y loga x:

В самом деле,

aloga xy = xy = aloga x y = ay loga x

и нужное равенство получим, приравняв показатели степени. 40: Если числа a и b положительны и не равны 1, то

loga b logb a = 1:

Действительно,

aloga b logb a = aloga b logb a = blogb a = a

и опять приравниваем показатели.

Если в качестве основания логарифма взято число e, то логарифм называют натуральным. Поэтому число e называют основанием натуральных логарифмов. Натуральный логарифм числа x обозначают ln x или log x.

Степенная функция. Функцию y = xa, где x > 0 и a –

произвольное число, называют степенн´ой функцией. Степенную функцию можно представить как сложную функ-

Из (4.7.1) в силу теоремы о непрерывности сложной функции вытекает непрерывность степенной функции.

Для положительных a степенную функцию xa доопределяют в нуле, положив 0a := 0. Тогда функция y = xa становится непрерывной на [0; +1).

На рисунке изображены графики степенной функции при различных значениях показателя a.

В случае, когда a – целое число, функцию xa рассматривают при любых x. При этом по определению считают x0 1 при всех x, в том числе и при x = 0. Для целых значений показателя a функция xa является чётной или нечётной в зависимости от чётности или нечётности a.

Если a – нечётное число, то для положительных a функция xa обратима при всех x и для отрицательных a она обратима при всех x 6= 0.

Тригонометрические функции. Будем пользоваться определениями тригонометрических функций из школьного курса. Докажем их непрерывность.

Теорема 4.7.1. При любом x 6= 0 справедливо неравенство

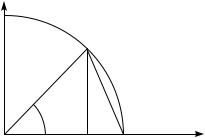
Доказательство. Пусть сначала 0 < x < =2. Рассмотрим окружность радиуса 1.

y

B

Рассмотрим угол \AOB, радианная мера которого равна x. Длина дуги ^ AB равна x, а sin x = BC. Но длина дуги ^ AB больше, чем длина хорды AB, а длина отрезка AB как гипотенузы прямоугольного треугольника 4ABC больше длины катета BC. Этим неравенство (4.7.2) доказано для 0 < x < =2.

Так как функции в левой и правой частях неравенства (4.7.2) чётные, то (4.7.2) справедливо и при =2 < x < 0. А если jxj >=2, то (4.7.2) следует из того, что j sin xj 6 1.

Теорема доказана.

Теорема 4.7.2. Каждая из функций y = sin x, y = cos x, y = tg x и y = ctg x непрерывна в своей области определения.

Доказательство. Начнём с функции y = sin x. Дадим аргументу приращение x и рассмотрим приращение функции:

Поэтому y ! 0 при x ! 0, что доказывает непрерывность синуса.

Непрерывность косинуса можно доказать аналогично, а можно воспользоваться равенством cos x = sin(x + =2) и теоремой о непрерывности сложной функции.

Непрерывность тангенса и котангенса получаем, сославшись на теорему о непрерывности частного.

Функция tg x на интервале ( =2; =2) непрерывна и строго возрастает от 1 до +1. Согласно теореме 4.5.2 значениями этой функции являются все действительные числа. Таким образом, функция y = tg x устанавливает взаимно однозначное соответствие интервалов ( =2; =2) и (1; +1).

В § 1.10 показано, что любой конечный интервал имеет мощность континуум. Теперь мы видим, что множество всех действительных чисел также имеет мощность континуум (об этом было сказано в § 1.10).

называют соответственно гиперболическим синусом, гиперболическим косинусом, гиперболическим тангенсом и гиперболическим котангенсом.

Они определены при всех x, исключение составляет гиперболический котангенс, который не определен в точке x = 0. Все гиперболические функции непрерывны в своей области определения. Это вытекает из теоремы о непрерывности сложной функции.

Графики гиперболических функций изображены на рисунке. Связь гиперболических функций с тригонометрическими, объясняющая, в частности, их названия, будет выяснена в даль-

нейшем.

Определение. Показательную, логарифмическую, степенную, основные и обратные тригонометрические функции, основные и обратные гиперболические функции и все функции, которые могут быть получены из перечисленных с помощью конечного числа арифметических действий и построения сложных функций, называют элементарными функциями.