
- •Введение
- •Глава 1 Действительные числа
- •1.1 Бесконечные десятичные дроби
- •1.2 Сравнение чисел
- •1.3 Точная верхняя и точная нижняя грани числового множества
- •1.4 Сложение чисел
- •1.5 Умножение чисел
- •1.6 Непрерывность множества действительных чисел
- •1.7 Последовательности вложенных отрезков
- •1.8 Дедекиндовы сечения
- •1.9 Об аксиоматическом определении действительных чисел
- •1.10 Счётные и несчётные множества
- •Глава 2 Предел последовательности
- •2.1 Определение предела последовательности
- •2.3 Арифметические свойства пределов
- •2.4 Бесконечно малые и бесконечно большие последовательности
- •2.5 Предел монотонной последовательности
- •2.6 Число e
- •2.7 Частичные пределы
- •2.8 Верхний и нижний пределы последовательности
- •2.9 Критерий Коши
- •Глава 3 Предел функции
- •3.1 Понятие функции
- •3.2 Определение предела функции
- •3.3 Свойства предела функции
- •3.4 Критерий Коши
- •3.5 Предел сложной функции
- •3.6 Односторонние пределы
- •3.7 Сравнение функций
- •Глава 4 Непрерывные функции
- •4.1 Непрерывность функции в точке
- •4.2 Классификация точек разрыва
- •4.3 Свойства функций, непрерывных на отрезке
- •4.4 Равномерная непрерывность функций
- •4.5 Непрерывность обратной функции
- •4.6 Показательная функция
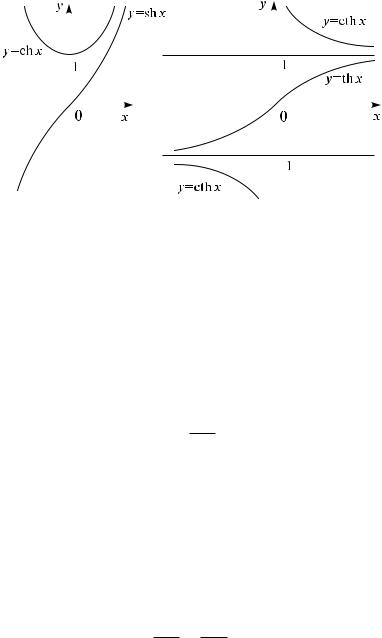
- •4.7 Элементарные функции
- •4.8 Примеры вычисления пределов
- •Глава 5 Производные и дифференциалы
- •5.1 Производная
- •5.2 Дифференциал функции
- •5.3 Производная обратной функции
- •5.4 Производная сложной функции
- •5.5 Производные и дифференциалы высших порядков
- •Глава 6 Свойства дифференцируемых функций
- •6.1 Локальные экстремумы функции
- •6.2 Теоремы о среднем
- •6.3 Раскрытие неопределённостей
- •6.4 Формула Тейлора
- •6.5 Формула Тейлора для элементарных функций
- •6.6 Исследование функций с помощью старших производных
- •6.7 Функции, выпуклые на промежутке
- •6.8 Некоторые классические неравенства
- •Глава 7 Кривые в трёхмерном пространстве
- •7.1 Векторнозначные функции
- •7.2 Определение кривой. Длина кривой
- •7.3 Гладкие кривые
- •Краткие сведения об ученых, упоминаемых в тексте
114 |
|
|
Гл. 4. Непрерывные функции |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В силу доказанных теорем каждая элементарная функция непрерывна в своей области определения.
§ 4.8. Примеры вычисления пределов
Рассматриваемые здесь пределы играют важную роль при изучении элементарных функций. В учебной и научно-популярной литературе эти пределы нередко называют “замечательными пределами”.
Пример 1. Найдём предел
lim sin x:
x!0 x
Здесь нельзя воспользоваться теоремой 3.3.1 о пределе частного, так как предел знаменателя равен нулю.
Поскольку речь идёт о пределе чётной функции, достаточно рассмотреть x 2 (0; =2).
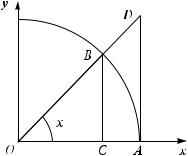
Будем опираться на геометрические соображения. Рассмотрим часть окружности радиуса 1 с центром в начале координат, расположенную в первом квадранте.
Пусть радианная мера угла AOB равна x. Из подобия прямоугольных треугольников AOD и COB находим
sinADx = cos1 x;
§ 4.8. Примеры вычисления пределов |
115 |
т. е. AD = tg x. Значит, площадь треугольника AOD равна |
|
||||||||||||
|
1 |
|
tg x: |
|
|||||||||
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||
Площадь кругового сектора AOB равна x=2, поэтому |
|
||||||||||||
|
x |
< |
|
1 |
|
tg x: |
|
||||||
2 |
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||
Отсюда |
|
|
|
sin x |
|
|
|||||||
cos x < |
: |
|
|||||||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
||
Согласно (4.7.2) sin x < x. Следовательно, |
|
||||||||||||
cos x < |
sin x |
< 1: |
|
||||||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
x |
|
||||
Так как функция cos x непрерывна, то cos x ! 1 при x ! 0. |
|||||||||||||
Поэтому согласно теореме 3.3.4 |
|
|
|
|
|
|
|
|
|||||
lim |
sin x |
= 1: |
(4.8.1) |
||||||||||
|
|||||||||||||
x!0 |
x |
|
|||||||||||
Пример 2. Покажем, что |
|
|
|
|
|
|
|
|
|||||
lim (1 + x)1=x = e: |
(4.8.2) |
||||||||||||
x!0 |
|
|
|
|
|
|
|
|
|||||
В § 2.6 доказано, что для x = 1=n, n 2 N, такой предел при n ! 1 существует. Он был взят в качестве определения числа e.
При доказательстве равенства (4.8.2) будет использована функция, которую называют целой частью числа. Обычно эту функцию обозначают [x]. По определению
[x] := max n:
n6x; n2Z

116 |
|
|
|
|
|
Гл. 4. |
Непрерывные функции |
||||
Таким образом, [x] – наибольшее целое число, не превосходящее x, |
|||||||||||
т. е. [x] 6 x < [x] + 1. График функции [x] имеет вид |
|
|
|||||||||
Если x > 0, то |
|
|
|
|
|
|
|
|
|
|
|
(1 + x)1=x = 1 + |
1 |
|
1=x |
< 1 + |
1 |
|
[1=x]+1 |
|
|||
|
|
|
|
= |
|
||||||
1=x |
|
|
|
[1=x] |
|
|
|||||
= 1 + |
1 |
|
|
[1=x] |
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
[1=x] |
|
|
1 + [1=x] : |
|
|
||||||
Предел полученного выражения при x ! +0 равен e. С другой |
|||||||||||
стороны, |
|
|
|
|
|
|
|
|
|
|
|
(1 + x)1=x > 1 + [1=x1] + 1 [1=x] = |
|
|
|
|
|
||||||
= 1 + [1=x1] + 1 |
[1=x]+1 1 + [1=x1] + 1 |
1 |
: |
||||||||
Предел этого выражения при x ! +0 также равен e. Таким обра- |
|||||||||||
зом, в силу теоремы 3.3.4 равенство (4.8.2) доказано для x ! +0. |
|||||||||||
Пусть теперь x < 0. Будем считать, что x 2 ( 1; 0). Имеем |
|||||||||||
(1 + x)1=x = (1 jxj) 1=jxj = 1 jxj |
1=jxj |
1 + |
1 j jjxj |
1=jxj |
||||||||||||
= |
= |
|||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
1 jxj |
|
|
|
|
|
|
|
|
|
|
||
= 1 + 1 j |
jjxj |
|
|
|
1 + 1 j jjxj : |
|
|
|
|
|||||||
|
x |
|
|
|
jxj |
|
|
|
|
x |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Но если x ! 0, то дробь |
|
|
jxj |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
! 0: |
|
|
|
|
|
|
||||
|
|
|
|
1 x |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
j |
j |
|
|
|
|
|
|
||||

§ 4.8. Примеры вычисления пределов |
117 |
При x 2 ( 1; 0) эта дробь положительна, поэтому в силу доказанного уже для x > 0 равенства (4.8.2) получаем его и при x < 0.
Пример 3. Пусть a > 0 и a 6= 1. Найдём предел
|
|
|
lim |
|
loga(1 + x) |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||||
|
|
|
x!0 |
|
|
|
|
|
|
|
|
|
|
||||||
Пользуясь непрерывностью логарифмической функции и ра- |
|||||||||||||||||||
венством (4.8.2), имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
lim |
loga(1 + x) |
= lim log |
a |
(1 + x)1=x |
= |
|
|
|
|
||||||||||
|
|
|
|
|
|||||||||||||||
x!0 |
x |
x!0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||||
|
|
|
= log |
|
|
lim (1 + x)1=x |
|
= log |
|
e = |
: |
||||||||
|
|
|
|
|
|
ln a |
|||||||||||||
Таким образом, |
|
|
a |
x!0 |
|
|
|
|
a |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
loga(1 + x) |
1 |
|
|
|
|
|
|
||||||||
|
|
|
lim |
|
|
|
|
|
|
|
= |
|
|
|
; |
|
|
|
(4.8.3) |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||
в частности, |
|
x!0 |
|
|
|
|
|
|
ln a |
|
|
|
|
||||||
|
|
|
|
ln(1 + x) |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
lim |
= 1: |
|
|
|
|
|
(4.8.4) |
|||||||||
|
|
|
|
|
x |
|
|
|
|
|
|||||||||
|
|
|
x!0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 4. Вычислим предел
lim ax 1;
x!0 x
считая a > 0 и a 6= 1.
Положим t := ax 1. Тогда ax = 1+t и x = loga(1+t). Значит,
|
|
ax 1 |
= |
|
|
|
t |
: |
|
|||
|
x |
loga |
(1 + t) |
|
||||||||
|
|
|
|
|
|
|
||||||
При x ! 0 в силу непрерывности показательной функции име- |
||||||||||||
ем t ! 0. Поэтому с помощью (4.8.3) находим |
|
|||||||||||
lim |
ax 1 |
= lim |
|
|
t |
|
= ln a: |
(4.8.5) |
||||
|
|
|
|
|
||||||||
x!0 |
x |
t!0 loga(1 + t) |
|
|||||||||
В частности, |
|
|
|
|
ex 1 |
|
|
|
|
|
||
|
|
lim |
|
|
= 1: |
|
|
(4.8.6) |
||||
|
|
x |
|
|
||||||||
|
|
x!0 |
|
|
|
|
|
|||||
