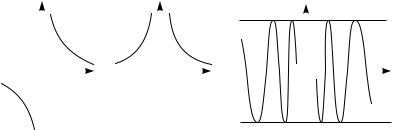
Если разрыв функции в точке не является разрывом первого рода, его называют разрывом второго рода. На следующем рисунке изображены некоторые характерные примеры точек разрыва второго рода.

§ 4.3. Свойства функций, непрерывных на отрезке

Определение. Функцию называют непрерывной на отрезке

[a; b], если она непрерывна во всех точках интервала (a; b), т. е. во внутренних точках отрезка, непрерывна справа в точке a и непрерывна слева в точке b.

Множество непрерывных на отрезке [a; b] функций обозначают C[a; b] и, если f непрерывна на [a; b], пишут f 2 C[a; b].

Наряду с непрерывностью на отрезке рассматривают непрерывность функций на интервале, на полуотрезке, полуоси и всей оси. Множество функций, непрерывных на интервале (a; b), обозначают C(a; b). Обозначения в остальных случаях аналогичны.

Когда ясно, о непрерывности на каком промежутке идёт речь, пишут f 2 C.

Понятно, что если функции f(x) и g(x) непрерывны на промежутке [a; b], то на [a; b] непрерывны функции f(x) g(x), f(x) g(x), а если g(x) не обращается в нуль на этом промежутке, то непрерывна и функция f(x)=g(x).

Теорема 4.3.1. Если функция непрерывна на отрезке, то она ограничена на этом отрезке.

[a; b] означает существование такого числа L, что jf(x)j 6 L при всех x 2 [a; b].

Докажем теорему от противного. Предположим, что функция f 2 C[a; b], но не является ограниченной на [a; b]. Тогда для каждого n 2 N существует такая точка xn 2 [a; b], что jf(xn)j > n. Таким образом, limn!1 f(xn) = 1.

Последовательность точек fxng ограничена, так как все они принадлежат отрезку [a; b]. Значит, по теореме Больцано–Вей- ерштрасса существует сходящаяся подпоследовательность fxnk g. Пусть := limk xnk , тогда 2 [a; b].

В силу непрерывности функции f в точке (если – один из концов отрезка, имеется в виду односторонняя непрерывность) для любой сходящейся к последовательности точек ftkg из [a; b]

имеем limk f(tk) = f( ).

Значит, limk!1 f(xnk ) = f( ). Но из limn!1 f(xn) = 1 следует равенство limn!1 f(xnk ) = 1 и мы пришли к противоречию.

Теорема доказана.

Отметим, что для функций, непрерывных на интервале, утверждение, подобное теореме 4.3.1, не верно. Это видно на примере функции 1=x, которая на интервале (0; 1) непрерывна, но неограничена.

Теорема 4.3.2 (Теорема Вейерштрасса). Если функция непрерывна на отрезке [a; b], то в некоторых точках этого отрезка она достигает точную верхнюю и точную нижнюю грани своих значений на [a; b].

Доказательство. Докажем достижимость точной верхней грани. Заметим, что точная верхняя грань значений функции существует, так как согласно теореме 4.3.1 из непрерывности функции на отрезке следует её ограниченность.

Пусть f 2 C[a; b] и M := supx2[a;b] f(x). Для каждого натурального n существует точка xn 2 [a; b] такая, что f(xn) >

M 1=n. Так как f(xn) 6 M при всех n, то

Последовательность fxng согласно теореме Больцано–Вейер- штрасса имеет сходящуюся подпоследовательность fxnk g. Пусть

:= limk xnk , тогда 2 [a; b].

Так как f непрерывна в точке , то limk!1 f(xnk ) = f( ).

Аиз (4.3.1) следует, что limk!1 f(xnk ) = M. Значит, M = f( ). Для точной нижней грани рассуждения аналогичны.

Теорема доказана.

Таким образом, можно говорить о максимальном значении функции, непрерывной на отрезке, и писать в этом случае не

supx2[a;b] f(x) а maxx2[a;b] f(x).

Для функций, непрерывных на интервале, утверждение, подобное теореме 4.3.2, не имеет места, даже если дополнительно предполагать ограниченность функции.

Теорема 4.3.3 (Теорема Коши о промежуточных значениях). Пусть функция f(x) непрерывна на отрезке [a; b] и f(a) 6= f(b). Тогда для любого числа c, заключённого между f(a) и f(b), существует точка 2 [a; b] такая, что c = f( ).

Доказательство. Рассмотрим сначала случай, когда числа f(a) и f(b) имеют разные знаки и c = 0.

Разделим отрезок [a; b] пополам. Если в точке деления значение функции равно нулю, то в качестве можно взять эту точку деления.

А если в точке деления значение функции f отлично от нуля, то в концах одного из получившихся отрезков значения f имеют разные знаки. Обозначим этот отрезок [a1; b1]. Заметим, что b1 a1 = (b a)=2.

Делим теперь отрезок [a1; b1] пополам и повторяем предыдущее рассуждение. То есть если в точке деления функция обращается в нуль, то нужная точка уже найдена. В противном случае выбираем тот из полученных отрезков, в концах которого функция принимает значения разных знаков. Обозначим этот отрезок [a2; b2], его длина в два раза меньше длины отрезка [a1; b1].

Продолжим этот процесс. Если мы не встретим нуль функции на каком-то шаге, то получим последовательность вложенных отрезков f[an; bn]g, длины которых bn an = (b a)=2n стремятся к нулю. Значит, согласно теореме 1.7.1 существует точка , принадлежащая всем этим отрезкам.

Покажем, что f( ) = 0. Если бы это было не так, то функция f сохраняла бы знак в некоторой окрестности точки . При достаточно больших n отрезки [an; bn] целиком содержатся в этой окрестности, так как она содержит точку , а длины отрезков

стремятся к нулю. Поскольку в концах отрезков [an; bn] значения функции f имеют разные знаки, мы пришли к противоречию с тем, что функция сохраняет знак в указанной окрестности точки .

Чтобы доказать теорему Коши в общем случае, введём функцию g(x) := f(x) c. Функция g непрерывна на отрезке [a; b] и в его концах принимает значения разных знаков. Значит, по уже доказанному существует точка 2 [a; b], в которой g( ) = 0. Таким образом, f( ) c = 0 и f( ) = c.

Теорема доказана.

Следствие 4.3.4. Пусть [a; b] – некоторый промежуток, т. е. отрезок, интервал или полуотрезок, и функция f непрерывна на этом промежутке. Положим

M := sup f(x);

x2[a;b]

если значения f на [a; b] ограничены сверху, и M := +1 в противном случае. Аналогично

m := inf f(x)

x2[a;b]

или m := 1.

Тогда для каждого числа c 2 (m; M) существует точка 2 [a; b] такая, что c = f( ).

Доказательство. Согласно определению точной верхней

грани в промежутке [a; b] имеется точка x такая, что c < f(x ) 6 M.

Точно также имеется такая точка x , что m 6 f(x ) < c. Рассмотрим след функции f на отрезке с концами в точках x

и x . Так как f непрерывна на этом отрезке, а в его концах имеет значения, между которыми лежит c, то согласно теореме 4.3.3 в некоторой точке отрезка функция f принимает значение c, что и требовалось доказать.

Следовательно, для функции f, непрерывной на произвольном промежутке, образом этого промежутка при отображении, осуществляемом функцией f, является некоторый промежуток.

Если в следствии 4.3.4 промежуток [a; b] является отрезком, то в силу теоремы 4.3.1 величины m и M конечны, а согласно теореме 4.3.2 они являются значениями функции f. Значит, в этом случае значения f целиком заполняют отрезок [m; M].