
ДПА-11-2014-1
.pdf
Вариант 72
Часть первая
Задания 1.1 – 1.16 содержат по четыре варианта ответов, из которых только ОДИН ответ ПРАВИЛЬНЫЙ. Выберите правильный, по Вашему мнению, ответ и отметьте его в бланке ответов.
1.1. Упростите выражение  6 b .
6 b .
А) 12 b ; |
Б) 7 b ; |
В) 6 b ; |
|
Г) 8 b . |
|||||||||
|
|
|
|
|
|
1 |
1 |
|
|
|
|||
1.2. Представьте в виде степени выражение q |
4 |
:q 5 . |
|
|
|
||||||||
1 |
|
5 |
|
4 |
|
|
|
1 |
|
||||
А) q |
20 |
; |
Б) q |
4 |
; |
В) q |
5 |
; |
|
Г) q |
10 |
. |
|
1.3. Укажите верное неравенство. |
|
|
|
|
|
|
|
|
|||||
А) sin100° < 0; |
Б) cos200° > 0; |
В) tg160° > 0; |
Г) ctg220° > 0. |
||||||||||
1.4.Множеством решений какого из неравенств является множество действительных чисел?
А) 2x > −1; |
Б) 2x < −1; |
В) 2x >1; |
|
Г) 2x <1. |
|||
1.5. Вычислите значение выражения |
lg25+ lg4. |
|
|
|
|||
А) 100; |
Б) lg29; |
В) 2; |
|
Г) 10. |
|||
1.6. Упростите выражение sin(α −β) + sinβcosα . |
|
|
|
||||
А) cosαsinβ ; |
Б) cosαcosβ ; |
В) sinαcosβ ; |
Г) |
sinαsinβ. |
|||
1.7. Найдите общий вид первообразных функции |
f (x) = e4x . |
||||||
А) 15e5x +C ; |
|
|
|
В) 4e4x +C ; |
|
|
|
Б) e4x +C ; |
|
|
|
Г) 14e4x +C . |
|
|
|
1.8. Сколько критических точек имеет функция f |
(x) = 1 x2 |
− 9x ? |
|||||
|
|
|
|
|
2 |
|
|
А) три точки; |
|
|
|
В) одну точку; |
|
|
|
Б) две точки; |
|
|
|
Г) ни одной точки. |
|
|
|
1.9. Решите неравенство |
x + 2 |
≥ 0. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
x −5 |
|
|
|
|
|
А) (−∞; −5] [2; +∞); |
В) [–2; 5); |
|
|
|
|||
Б) (−∞; −2] (5; +∞) ; |
Г) [–2; 5]. |
|
|
|
|||
161
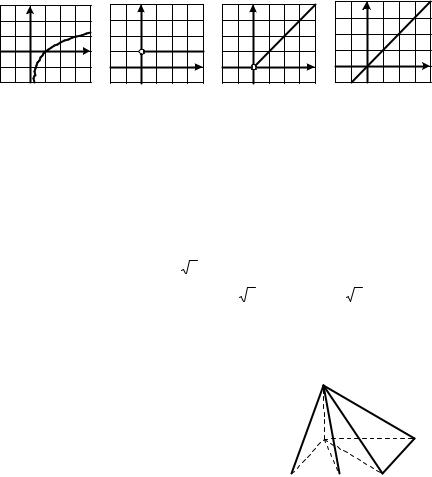
1.10. На одном из рисунков изображен график функции y = 3log3 x . Укажите этот рисунок.
А) |
y |
|
Б) |
y |
|
В) |
y |
|
Г) |
y |
|
|
|
1 |
|
|
1 |
|
|
1 |
|
|
1 |
|
|
|
0 |
1 |
x |
|
|
|
|
|
|
|||
|
0 |
1 |
x |
0 |
1 |
x |
0 |
1 |
x |
|||
|
|
|
|
1.11. Оркестру требуются скрипач, пианист и флейтист. На место скрипача есть 7 кандидатов, на место пианиста — 5, а на место флейтиста — 2. Сколько существует вариантов нового состава оркестра?
А) 14; |
Б) 35; |
В) 50; |
Г) 70. |
1.12. Цену товара сначала снизили на 20 %, а потом повысили на 20 %. Как изменилась цена товара по сравнению с первоначальной?
А) не изменилась; |
В) увеличилась на 4 %; |
||
Б) уменьшилась на 4 %; |
Г) уменьшилась на 2 %. |
||
1.13. Периметр квадрата равен 20 |
2 см. Найдите его диагональ. |
||
А) 5 см; |
Б) 10 см; |
В) 5 2 см; |
Г) 10 2 см. |
1.14. Сколько сторон имеет правильный многоугольник, угол которого ра-
вен 150°?
А) 12; |
Б) 15; |
В) 18; |
Г) 20. |
|
|||
1.15. Основанием пирамиды MABCD, изобра- |
M |
|
|||||
женной на рисунке, является прямоугольник, |
|
|
|||||
боковое ребро MB перпендикулярно плос- |
|
|
|||||
кости основания пирамиды, точка E — се- |
B |
C |
|||||
редина ребра AD. Укажите линейный угол |
|
|
|||||
двугранного угла с ребром AD. |
A |
|
D |
||||
А) MAB; |
В) MDB; |
E |
|||||
|
|
||||||
|
|
|
|||||
Б) MEB; |
Г) MCB. |
|
|
|
|||
|
|
|
JJJG |
|
|
|
|
1.16. Найдите координаты вектора AF , если A(5;–3;–7), F(1;–5;3). |
|
||||||
А) |
JJJJG |
В) |
JJJG |
|
|
||
AF |
(4; 2; –10); |
AF (6; –8; –4); |
|
||||
Б) |
JJJJG |
Г) |
JJJG |
|
|
||
AF |
(–4; –2; 10); |
AF (–4; –8; –4). |
|
||||
162

Вариант 73
Часть первая
Задания 1.1 – 1.16 содержат по четыре варианта ответов, из которых только ОДИН ответ ПРАВИЛЬНЫЙ. Выберите правильный, по Вашему мнению, ответ и отметьте его в бланке ответов.
1.1. Упростите выражение sin(32π +α). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
А) sinα; |
|
Б) –sinα; |
В) cosα ; |
Г) –cosα . |
|
|
|
|||||||||||||||||
1.2. Решите уравнение 2x = |
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
А) –3; |
|
Б) 3; |
8 |
|
|
В) –4; |
|
|
Г) 4. |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
1.3. Укажите область определения функции y = 4 x −16 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
А) [–16; +∞); |
Б) [16; +∞); |
В) [–2; +∞); |
Г) [2; +∞). |
|
|
|
||||||||||||||||||
1.4. График какой из функций изображен на ри- |
|
|
|
|
y |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
сунке? |
|
В) y = log3 x ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
А) y = 3 x ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||
Б) y = x3 ; |
|
Г) y = 3x . |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
a |
a . |
|
|
|
|
|
|
|
|
1 |
|
x |
||
1.5. Представьте в виде степени выражение |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4 |
|
|
1 |
7 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
А) a |
3 |
; |
Б) |
a 3 ; |
В) a |
6 |
; |
Г) a |
6 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.6. Вычислите интеграл ∫x3 dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А) 1 ; |
|
Б) − 1 |
; |
|
|
В) |
1 |
; |
|
|
Г) − 1 . |
|
|
|
||||||||||
3 |
|
|
|
3 |
|
|
|
|
4 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|||
1.7. Чему равно значение выражения lgtgx + lgctgx? |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
А) 100; |
|
Б) 10; |
|
|
|
В) 1; |
|
|
Г) 0. |
|
|
|
||||||||||||
1.8. Найдите производную функции |
y = ex cosx . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
А) y'= ex sin x ; |
|
|
|
|
В) |
y'= ex (cosx +sin x) ; |
|
|
|
|||||||||||||||
Б) y'= −ex sin x ; |
|
|
|
Г) |
y'= ex (cosx −sin x) . |
|
|
|
||||||||||||||||
1.9. В какой координатной четверти находится вершина параболы
y = (x +8)2 −16? |
|
А) в I четверти ; |
В) в ІІІ четверти ; |
Б) во ІІ четверти ; |
Г) в ІV четверти . |
163
1.10. Решите неравенство x2 < x . |
|
Г) (−∞;0) (1; +∞) . |
|
А) (–∞; 1); |
Б) (–∞; 0); |
В) (0; 1); |
|
1.11. Из натуральных чисел от 1 до 18 включительно ученик наугад называет одно. Какова вероятность того, что это число является делителем
числа 18? |
|
|
|
|
|
|
|
|
|
||
А) |
1 |
; |
Б) |
|
5 |
; |
В) |
2 |
; |
Г) |
1 . |
|
2 |
|
|
18 |
|
|
9 |
|
|
3 |
|
1.12. Цену на некоторый товар последовательно снизили на 10 %, на 20 %
и на 25 %. На |
сколько процентов |
снизилась |
цена |
по сравнению |
||
с первоначальной? |
|
|
|
|
|
|
А) на 46 %; |
Б) на 54 %; |
В) на 55 %; |
Г) на 60 %. |
|||
1.13. Чему равна |
длина окружности, |
ограничивающей |
круг, |
площадь |
||
которого равна 16π см2? |
|
|
|
|
|
|
А) 4π см; |
Б) 8π см; |
В) 12π см; |
Г) 16π см. |
|
||
1.14. В треугольнике MND известно, что ND=10 см, |
sinM=0,8, |
sinD=0,4. |
||||
Найдите сторону MN. |
|
|
|
|
|
|
А) 8 см; |
Б) 16 см; |
В) 5 см; |
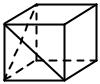
1.15. На рисунке изображен куб ABCDA1B1C1D1. Найдите угол между прямыми AB1 и A1D.
А) 30°; Б) 45°; В) 60°; Г) 90°.
1.16. При каком значении k векторы
m (5−2k ;6; −2) и n (k −4;6;−2) равны? А) –3; Б) 3; В) –9;
Г) 20 см.
B1 C1 A1 D1
B C A D
Г) 9.
164

Вариант 74
Часть первая
Задания 1.1 – 1.16 содержат по четыре варианта ответов, из которых только ОДИН ответ ПРАВИЛЬНЫЙ. Выберите правильный, по Вашему мнению, ответ и отметьте его в бланке ответов.
1.1. Графику какой из функций принадлежит точка A(16;−2)?
А) y = 4 x ; |
Б) y = 4 − x ; |
В) y = −4 x ; |
Г) y = −4 − x . |
1.2. Какое из данных неравенств является неверным?
А) sin100°< cos160° ; Б) cos100°< sin10° ;
1.3. Решите уравнение |
4x = 7 . |
||||||
А) |
7 |
; |
Б) |
|
4 |
; |
|
7 |
|||||||
|
4 |
|
|
|
|||
1.4. Чему равно значение выражения
А) 1 |
; |
Б) –8; |
8 |
|
|
1.5. Вычислите значение выражения
А) 2; Б) 5;
1.6.Найдите производную функции А) f '(x) = −tg3x ;
Б) f '(x) = −3tg3x ;
В) sin100°< tg100° ; Г) cos100°< cos180°.
В) log4 7 ; Г) log7 4.
(2−0,7)3 2−0,9 ?
В) 2; Г) –6.
log2 25
log2 5
В) 10; Г) 20. f (x) = ctg3x .
В) f '(x) = −sin12 3x ; Г) f '(x) = −sin32 3x .
2
1.7. Вычислите интеграл ∫x5 dx .
|
|
|
|
|
1 |
|
|
|
|
|
|
|
А) 75; |
|
Б) 12,6; |
|
В) 5,5; |
|
Г) 10,5. |
||||||
1.8. Решите уравнение cos2x = |
3 |
. |
|
|
|
|
||||||
2 |
π |
|
|
|||||||||
|
|
|
π |
|
πk |
|
|
|
|
|
||
А) (−1)k |
+ |
, k Z ; |
|
В) ± |
+2πk , k Z ; |
|||||||
|
6 |
|||||||||||
6 |
2 |
|
||||||||||
Б) ± |
π |
+πk , |
k Z ; |
|
Г) (−1)k |
π |
+πk , k Z . |
|||||
|
|
|||||||||||
|
|
|
||||||||||
12 |
|
|
|
|
|
12 |
|
|||||
1.9. В секторе футбольного стадиона каждый следующий ряд содержит на
3 места больше, |
чем предыдущий. Сколько |
рядов в секторе, если |
|
в первом ряду 32 места, а в последнем — 122 места? |
|||
А) 27 рядов; |
Б) 28 рядов; |
В) 30 рядов; |
Г) 31 ряд. |
165
1.10. Освободитесь от иррациональности в знаменателе дроби 384 .
А) 23 4 ; |
Б) 43 4 ; |
В) 43 2 ; |
Г) 23 2 . |
1.11. В классе a девочек и b мальчиков. Первым вызвали к доске мальчика. Какова вероятность того, что второй отвечать у доски будет девочка?
А) |
|
a |
|
; |
Б) |
|
a |
|
|
; |
В) |
a −1 |
; |
|
a |
+b |
a +b −1 |
a +b |
|
||||||||||
|
|
|
|
|
|
|
||||||||
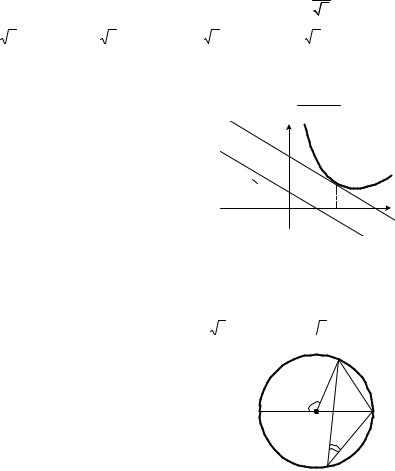
1.12. Прямые m и n, изображенные на ри- |
|
n |
||||||||||||
сунке, |
параллельны, причем прямая m |
|
||||||||||||
x |
|
|||||||||||||
является касательной к графику функ- |
|
|||||||||||||
|
+ |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
ции |
y = f (x) |
в точке с абсциссой x0 , |
|
|
y |
|||||||||
|
|
|
||||||||||||
а уравнение |
прямой n |
|
имеет |
вид |
|
|
|
|||||||
x +3y − 2 = 0. Найдите |
f '(x0). |
|
|
|
|
|||||||||
Г) a b+−b1−1 .
m |
y |
|
2 |
|
y = f (x) |
|
|
|
= |
|
|
|
0 |
x |
|
0 |
x0 |
А) – 1 |
; |
Б) 3; |
В) –2; |
Г) 1. |
3 |
|
|
|
|
1.13. Чему равна площадь треугольника DEF, если
D =150° ?
А) 40 см2; |
Б) 20 см2; |
В) 40 3 см2; |
1.14. На рисунке изображена окружность с центром O, хорда AB равна радиусу окружности. Чему равна разность α −β ?
А) 90°; Б) 60°; В) 45°; Г) 30°.
1.15. Вычислите площадь боковой поверхности прямой призмы, основанием которой является ромб со стороной 6 см, а высота призмы равна 12 см.
DE = 8см, DF =10см,
Г) 20 3 см2.
3 см2.
A
α
O B
β
А) 432 см2; |
Б) 72 см2; |
В) 144 см2; |
Г) 288 см2. |
||
1.16. Какой вектор коллинеарен вектору mJG (–2; –4; 1)? |
|
||||
А) aJG |
(–6; –12; –3); |
В) cG |
(–6; 12; –3); |
|
|
Б) bJG |
(6; 12; 3); |
|
Г) nG |
(6; 12; –3). |
|
166

Вариант 75
Часть первая
Задания 1.1 – 1.16 содержат по четыре варианта ответов, из которых только ОДИН ответ ПРАВИЛЬНЫЙ. Выберите правильный, по Вашему мнению, ответ и отметьте его в бланке ответов.
1.1. Представьте выражение a−1,4 :a1,6 |
в виде степени. |
|
|||
А) a0,2 ; |
Б) a−3 ; |
В) a− |
7 |
; |
Г) a3 . |
8 |
|||||
1.2. Упростите выражение cos(2π −α). |
|
|
|||
А) sinα ; |
Б) –sinα ; |
В) cosα ; |
Г) –cosα . |
||
1.3. Чему равно значение функции |
f (x) =3 x +15 в точке x0 = 12 ? |
||
А) 9; |
Б) 3; |
В) 27; |
Г) –3. |
1.4. Какое неравенство имеет решения? |
|
||
А) 10x < −10; |
Б) 10x ≤ 0 ; |
В) 10x < 0,01; |
Г) 10x2 < 0,1. |
1.5. Какое равенство является верным? |
|
||
А) |sin2| = sin2; |
|
В) |sin2| = cos2; |
|
Б) |sin2| = −sin2 ; |
Г) |sin2| = −cos2. |
||
1.6. График какой из функций не пересекает ось ординат?
А) y = 3x ; |
Б) y = (13)x ; |
В) y = x3 ; |
Г) y = log3 x . |
1.7.На одном из рисунков изображен график функции y = lg(−x). Укажите этот рисунок.
А) y |
|
|
Б) y |
|
|
В) |
y |
Г) |
y |
|
0 |
1 |
x |
0 |
1 |
x |
1 0 |
x |
1 0 |
x |
|
1.8. Найдите общий вид первообразных функции |
f (x) = x + 7. |
|
|
|||||||
А) |
x2 |
+ 7x + C ; |
В) |
x2 |
+ 7 +C ; |
||
2 |
2 |
|
|||||
|
|
|
|
|
|
||
Б) x2 + 7x + C ; |
Г) |
|
x2 |
|
+ C . |
||
|
2 |
||||||
|
|
|
|
|
|
|
|
1.9.Найдите номер члена арифметической прогрессии 8; 8,4; 8,8; ... , рав-
ного 12,4.
А) 9; |
Б) 10; |
В) 11; |
Г) 12. |
167

1.10. Найдите угловой коэффициент касательной к графику функции
f (x) = 3e−4x |
в точке с абсциссой x0 = 0 . |
|
|
А) –4; |
Б) –12; |
В) 3; |
Г) 0. |
1.11. Четыре однотипных станка-автомата обрабатывают 8 одинаковых деталей в минуту. За какое время три таких станка обработают 60 деталей?
А) 10 мин; |
Б) 8 мин; |
В) 7 мин; |
Г) 6 мин. |
1.12. Положительные числа a и b таковы, что число a составляет 50% от числа b. Сколько процентов число b составляет от числа a?
А) 25%; |
|
Б) 50%; |
В) 100%; |
Г) 200%. |
|
||
1.13. Дано: ∆MNK ~ ∆M1N1K1, стороны MN и M1N1 |
— соответственные, |
||||||
MN=6 см, |
M1N1=15 см. Найдите |
периметр треугольника MNK, если |
|||||
периметр треугольника M1N1K1 равен 40 см. |
|
|
|||||
А) 16 см; |
|
Б) 8 см; |
В) 20 см; |
Г) 100 см. |
|
||
1.14. В треугольнике ABC, изображенном на рисунке, |
B |
|
|||||
AB = BC . Найдите угол γ, если β = 36°. |
β |
|
|||||
|
|
|
|
|
|
||
А) 144°; |
Б) 120°; |
В) 110°; |
Г) 108°. |
|
|
||
1.15. Диагонали параллелограмма параллельны плос- |
A |
γ |
|||||
кости α. Каково взаимное расположение плос- |
C |
||||||
|
|||||||
кости α и плоскости параллелограмма? |
|
|
|||||
А) совпадают; |
|
|
В) параллельны; |
|
|
||
Б) пересекаются; |
|
|
Г) установить невозможно. |
|
|||
1.16. Точка K — середина отрезка MN, M(3;–1;4), K(2;5;–2). Найдите |
|||||||
координаты точки N. |
|
|
|
|
|||
А) N(5; 4; 2); |
Б) N(2,5; 2; 1); |
В) N(1; –6; 6); |
Г) N(1; 11; –8). |
||||
168
Вариант 76
Часть первая
Задания 1.1 – 1.16 содержат по четыре варианта ответов, из которых только ОДИН ответ ПРАВИЛЬНЫЙ. Выберите правильный, по Вашему мнению, ответ и отметьте его в бланке ответов.
1.1. Какое число является решением неравенства 3x > 9?
А) 1; |
|
|
|
|
|
Б) 1,5; |
|
В) 0,2; |
|
|
Г) 2,4. |
||||
1.2. Найдите значение выражения log |
2 |
1 |
. |
|
|
|
|
|
|
||||||
32 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
А) –5; |
Б) 5; |
|
В) 16; |
|
|
Г) 4. |
|||||||||
1.3. Решите уравнение sin4x = −1. |
|
|
|
|
|
|
|
|
|
||||||
А) − |
|
π |
+ 2πk , |
k Z ; |
|
В) − |
π |
+ |
πk |
, k Z ; |
|||||
|
2 |
|
|
|
|
8 |
|
2 |
|
||||||
Б) − |
π |
+ πk , k Z ; |
|
Г) − |
π |
|
+ πk , k Z . |
||||||||
4 |
|
|
|||||||||||||
|
|
|
|
|
|
8 |
|
|
|
|
|||||
1.4. Найдите производную функции f (x) = 7x . |
|||||||||||||||
А) f '(x) = 7x ; |
|
В) f '(x) = 7x ln7; |
|||||||||||||
Б) f |
'(x) = |
7x |
; |
|
Г) f '(x) = (x −1) 7x−1 . |
||||||||||
ln7 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.5.Вычислите площадь заштрихованной фигуры, изображенной на рисунке.
А) 1; |
Б) 2; |
В) |
1 |
; |
Г) 1 |
1 . |
|
|
|
2 |
|
|
2 |
1.6.Между какими двумя последовательными натуральными числами находится на коор-
y |
|
|
1 |
y = cosx |
|
0 |
π |
x |
|
2 |
|
динатной прямой число 3 40 ? |
|
|
|
А) 1 и 2; |
Б) 3 и 4; |
В) 2 и 3; |
Г) 4 и 5. |
1.7. Упростите выражение cos7α−cos3α . |
|
||
|
sin2α |
|
|
А) 2cos5α ; |
Б) –2cos5α ; |
В) –2sin5α; |
Г) 2sin5α. |
1.8. Какое неравенство выполняется при всех отрицательных значениях x?
А) x3 +1≤ 0 ; |
Б) x3 < −x3 ; |
В) − x3 < 0 ; |
Г) x3 > −x3. |
1.9. Решите уравнение 4 6log6 x = 5− x2 . |
|
||
А) –5; 1; |
Б) –1; 5; |
В) 1; |
Г) 5. |
169
1.10. Цена некоторого товара после двух последовательных повышений возросла на 68 %, причем в первый раз цена была повышена на 40 %. На сколько процентов была повышена цена во второй раз?
А) на 28 %; |
Б) на 14 %; |
В) на 30 %; |
Г) на 20 %. |
1.11. В ящике лежат 40 карточек, пронумерованных числами от 1 до 40. Какова вероятность того, что номер наугад взятой карточки будет кратным числу 8?
А) 1 ; |
Б) 1 ; |
В) |
1 |
; |
Г) |
|
1 |
. |
|
10 |
|||||||||
4 |
5 |
|
8 |
|
|
|
|||
1.12. Чему равно наименьшее значение функции |
f (x) =tg x cosx − 3? |
||||||||
А) такого значения не существует; |
|
|
В) –3; |
|
|
|
|||
Б) –4; |
|
|
|
Г) –2. |
|
|
|
||
1.13. Одно из оснований трапеции на 6 см меньше другого, а средняя линия трапеции равна 8 см. Найдите большее основание трапеции.
А) 5 см; |
Б) 11 см; |
В) 9 см; |
1.14. Отрезок BM — высота треугольника ABC, изображенного на рисунке. Чему равна площадь треугольника ABC ( длины отрезков на рисунке приведены в сантиметрах)?
А) 36 см2; |
В) 60 см2; |
Б) 72 см2; |
Г) 24 см2. |
Г) 12 см.
B
6 |
10 |
||
|
|
|
|
A 4 M |
|
C |
|
|
|||
1.15. Вычислите площадь боковой поверхности конуса, радиус основания которого равен 8 см, а образующая — 12 см.
А) 32π см2; |
Б) 48 см2; |
В) 48π см2; |
1.16. Сторона основания правильной четырехугольной пирамиды MABCD, изображенной на
рисунке, равна 2. Чему равен модуль вектора
JJJJG JJJJG
MC −MA ?
А) 2 2 ; Б) 2; |
В) 2 ; |
Г) 1. |
Г) 96π см2.
M
B C A
C A  D
D
170
