
ДПА-11-2014-1
.pdf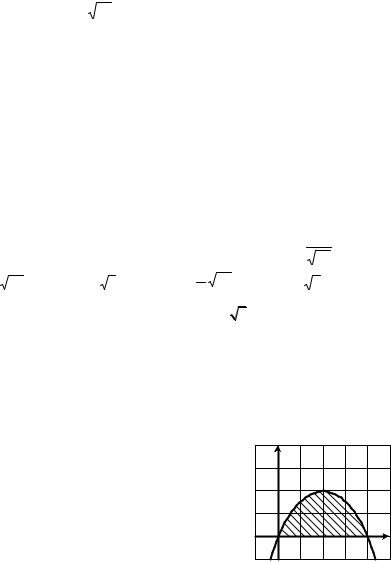
Вариант 47
Часть первая
Задания 1.1 – 1.16 содержат по четыре варианта ответов, из которых только ОДИН ответ ПРАВИЛЬНЫЙ. Выберите правильный, по Вашему мнению, ответ и отметьте его в бланке ответов.
1.1. Решите уравнение |
2x |
= 4. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
А) 1; |
|
Б) 2; |
|
В) 4; |
|
|
|
|
Г) 16. |
||||||||||||||
1.2. Сократите дробь |
a |
+27 |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
a3 +3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
2 |
|
1 |
|
|
1 |
|
|
|
|
|
|
2 |
1 |
|||
А) a |
3 |
+9; |
|
Б) a |
3 |
|
+3a 3 +9 |
; В) a |
3 +3; |
|
|
|
Г) a |
3 |
−3a 3 +9. |
||||||||
1.3. Решите уравнение |
sinx = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
А) |
π |
+πk , |
k Z ; |
|
|
|
|
В) 2πk , k Z ; |
|
|
|
|
|
|
|||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Г) π+ 2πk , k Z . |
|
|
|
|||||||||
Б) πk , k Z ; |
|
|
|
|
|
|
|
||||||||||||||||
1.4. Укажите область определения функции |
f (x) = log9(7− x) . |
||||||||||||||||||||||
А) (7; +∞); |
|
Б) (–∞; 7); |
В) [7; +∞); |
|
|
Г) (–∞; 7]. |
|||||||||||||||||
1.5. Освободитесь от иррациональности в знаменателе дроби |
|
18 . |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 27 |
|
А) 64 27 ; |
|
Б) 94 3 ; |
В) |
2 4 27 ; |
|
|
|
Г) 64 3 . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
1.6. Укажите область значений функции |
y = 7+ 4 x . |
|
|
|
|
|
|
||||||||||||||||
А) [7; +∞); |
|
Б) [0; +∞); |
В) [0; 3]; |
|
|
|
Г) (–∞; +∞). |
||||||||||||||||
1.7. Найдите производную функции |
f (x) = tg3x . |
|
|
|
|
|
|
|
|
||||||||||||||
А) |
f '(x) = 3ctg3x ; |
|
|
|
|
В) |
f '(x) = |
|
3 |
|
; |
|
|
|
|
||||||||
|
|
|
|
cos2 3x |
|
|
|
||||||||||||||||
Б) |
f '(x) = |
1 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
Г) |
f '(x) = − |
3 |
|
|
|
. |
|
|
|||||||||||
cos23x |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
2 |
3x |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|||
1.8.Вычислите площадь заштрихованной фигуры, изображенной на рисунке.
А) |
4 |
; Б) |
20 ; |
В) |
2 |
; |
Г) |
14 . |
3 |
|
3 |
3 |
|
|
3 |
||
1.9. Упростите |
выражение 6−| a −3|, если a < 3. |
|||||||
А) 9 – a; |
Б) 3 – a; |
В) a + 9; |
|
Г) a + 3. |
||||
1.10. Найдите разность арифметической прогрессии (an), если a4 = 8 , a9 = 23.
y |
|
|
|
1 |
|
y = 2x − x2 |
|
|
|
|
|
0 |
1 |
2 |
x |
А) 3; |
Б) 4; |
В) 3,5; |
Г) 4,5. |
111
1.11. Средняя высота 10 домов равна 60 м, а средняя высота четырех из них — 48 м. Чему равна средняя высота остальных 6 домов?
А) 60 м; Б) 64 м; В) 68 м; Г) 72 м.
1.12. Сколько четырехзначных чисел, цифры которых могут повторяться, можно записать, используя цифры 1, 2, 3 и 4?
А) 24; |
Б) 64; |
В) 256; |
Г) 128. |
1.13. Найдите сторону ромба, диагонали которого равны 24 см и 18 см.
А) 30 см; |
Б) 15 см; |
В) 21 см; |
1.14. Отрезки AB и CD, изображенные на рисунке, параллельны. Чему равна сумма углов α и β?
А) 60°; |
В) 150°; |
Б) 120°; |
Г) найти невозможно . |
Г) 27 см.
A α |
B |
|
|
60° |
|
C |
β |
D |
|
||
1.15. Точка M удалена от плоскости α на 15 см. Из этой точки проведена к плоскости α наклонная MK. Найдите длину этой наклонной, если ее
проекция на плоскость α равна 8 см. |
|
||
А) 16 см; |
Б) 17 см; |
В) 19 см; |
Г) 23 см. |
1.16. Найдите координаты середины отрезка AB, если A(8;3;–4), B(6;7;–2). |
|||
А) (7; 5; –3); |
Б) (1; –2; –1); |
В) (7; –2; –3); |
Г) (–1; 5; –1). |
112
Вариант 48
Часть первая
Задания 1.1 – 1.16 содержат по четыре варианта ответов, из которых только |
||||||||||||||||||||
ОДИН ответ ПРАВИЛЬНЫЙ. Выберите правильный, по Вашему мнению, |
||||||||||||||||||||
|
|
|
|
|
|
ответ и отметьте его в бланке ответов. |
||||||||||||||
1.1. Решите неравенство log0,2 x < log0,2 6. |
|
|
|
|||||||||||||||||
А) (0; 6); |
|
|
|
|
Б) (–∞; 6); |
|
В) (6; +∞); |
Г) (–∞; +∞). |
||||||||||||
1.2. Вычислите значение выражения |
cos126°cos36°+sin126°sin36° . |
|||||||||||||||||||
А) 0; |
|
|
|
|
Б) –1; |
|
|
|
|
|
В) 1; |
|
|
Г) 1 . |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1.3. Решите уравнение 102−x |
= 1000 . |
|
|
|
|
|
|
|
||||||||||||
А) –1; |
|
|
|
|
Б) 1; |
|
|
|
|
|
В) 5; |
|
|
Г) –2. |
||||||
1.4. Чему равно значение выражения |
32 −4 (−9)2 |
? |
||||||||||||||||||
А) 2 3 ; |
|
|
|
|
Б) 0; |
|
|
|
|
|
В) 6; |
|
|
Г) 12. |
||||||
|
|
|
|
|
|
|
1 |
|
1 |
+9 |
|
|
|
|
|
|
|
|
||
1.5. Сократите дробь |
|
m2 −6m |
4 |
. |
|
|
|
|
|
|
|
|||||||||
|
1 |
|
9 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
m2 |
− |
|
|
|
|
|
|
|
|
|
|
|
А) −6m4 |
; |
|
|
Б) m4 |
−3; |
|
1 |
|
|
; |
|
1 |
||||||||
|
|
|
В) m1 +3 |
|
Г) m1 −3 . |
|||||||||||||||
1 |
|
|
|
|
1 |
|
|
|
|
|
4 |
|
|
|
|
4 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m4 −3 |
|
|
m4 +3 |
|||
1.6. Решите уравнение sin5x = |
3 |
. |
|
|
|
|
|
|
|
|||||||||||
2 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
π |
|
πk |
|
|
|
|
|
|
|
|
|
|
π |
|
+ πk , k Z ; |
|
А) (−1)k |
+ |
, k Z ; |
|
|
|
|
В) (−1)k |
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
15 |
|
5 |
|
|
|
|
|
|
|
30 |
|
5 |
|||||
Б) ± |
π |
+ |
|
2πk , k Z ; |
|
|
|
|
|
Г) ± |
π |
+ |
2πk , k Z . |
|||||||
|
|
|
|
|
|
|
|
|||||||||||||
15 |
|
5 |
|
|
|
|
|
|
|
|
30 |
|
|
5 |
|
|||||
1.7. Сколько нулей имеет функция f (x) =16− x4 ? |
|
|||||||||||||||||||
А) ни одного; |
|
Б) один; |
|
|
|
В) два; |
|
|
Г) четыре. |
|||||||||||
1.8. Укажите область определения функции y = log−x 2. |
||||||||||||||||||||
А) (–∞; –1); |
|
|
|
|
|
|
|
|
В) (–∞; 0); |
|
||||||||||
Б) (−∞; −1) (−1; 0) ; |
|
|
|
|
|
Г) (–∞; +∞). |
||||||||||||||
113
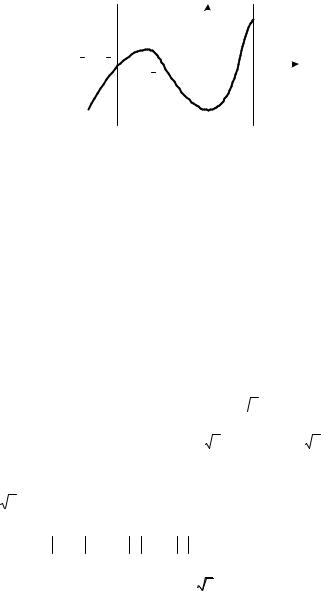
1.9. Функция y = f (x) определена на промежутке [–8; 3] и имеет производную в каждой точке области определения. На рисунке изображен
график функции |
y = f '(x) . |
Определите |
промежутки возрастания |
||||||||||||||||
функции y = f (x) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
А) [–8; –4] и [0; 3]; |
|
|
|
|
|
В) [–3; 1]; |
|
|
|
|
|
|
|||||||
Б) [–6; –3] и [2; 3]; |
|
|
|
|
|
Г) определить невозможно. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
0 |
|
|
|
2 |
3 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.10. Вероятность не выиграть в лотерею ни одного приза, приобретя один лотерейный билет, составляет 0,92. Сколько призов разыгрывается в лотерею, если выпущено 10 000 лотерейных билетов?
А) 80 призов; |
Б) 800 призов; |
В) 920 призов; |
Г) 92 приза. |
1.11. Укажите множество значений функции y = x2 −4x +3. |
|||
А) [–1; +∞); |
Б) [–7; +∞); |
В) [–2; +∞); |
Г) [–3; +∞). |
1.12.Цену товара сначала повысили последовательно на 10 % и на 20 %,
апотом снизили на 15 %. Как изменилась цена товара по сравнению
спервоначальной?
А) увеличилась на 12,2 %; |
В) уменьшилась на 10,8 %; |
||
Б) увеличилась на 15 %; |
Г) не изменилась. |
|
|
1.13. Диагонали прямоугольника ABCD пересекаются в точке O, AB=3 см, |
|||
AC=8 см. Найдите периметр треугольника AOB. |
|
||
А) 22 см; |
Б) 16 см; |
В) 7 см; |
Г) 11 см. |
1.14. В треугольнике ABC известно, что AC = 4 2 см, A=30°, B=45°. Найдите сторону BC.
2 см, A=30°, B=45°. Найдите сторону BC.
А) 8 см; |
Б) 4 см; |
В) 4 3 см; |
Г) 8 3 см. |
1.15. Вычислите объем призмы, основанием которой является параллелограмм со сторонами 6 см и 4 см и углом 45°, а высота призмы рав-
на 7 2 см. |
|
|
|
А) 70 см3; |
Б) 84 см3; |
В) 56 см3; |
Г) 168 см3. |
1.16. Вычислите aJG−bJG , если aG = 2 , bG =1, угол между векторами aG и bG
равен 120°. |
|
|
|
А) 1; |
Б) 7; |
В) 7 ; |
Г) 3. |
114

Вариант 49
Часть первая
Задания 1.1 – 1.16 содержат по четыре варианта ответов, из которых только ОДИН ответ ПРАВИЛЬНЫЙ. Выберите правильный, по Вашему мнению, ответ и отметьте его в бланке ответов.
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|||
1.1. Представьте в виде степени выражение a4 |
:a6 . |
|
|
|||||||||||||
3 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|||||
А) a |
2 |
; |
Б) a |
12 |
; |
|
|
В) a |
24 |
|
; |
|
|
Г) a 3 . |
||
1.2. Упростите выражение |
2cos2 3α −1. |
|
|
|
|
|
||||||||||
А) sin2 3α; |
Б) –sin2 3α; |
В) –cos6α ; |
Г) cos6α . |
|||||||||||||
1.3. График какой из функций пересекает ось абсцисс? |
|
|
||||||||||||||
А) f (x) = 4x ; |
Б) f (x) = |
x |
; |
В) f (x) = 4x ; |
Г) f (x) = 4 . |
|||||||||||
4 |
||||||||||||||||
1.4. Решите уравнение 3tg x +12 = 0. |
|
|
|
|
|
|
|
|
||||||||
А) arctg4+ πk , |
k Z ; |
|
|
|
В) − 1arctg12+ |
πk |
, k Z ; |
|||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
||
Б) –arctg4+ 2πk , k Z ; |
Г) –arctg4+ πk , |
k Z . |
||||||||||||||
1.5. Чему равна сумма целых решений неравенства |
x −4 |
≤ 0 ? |
||||||||||||||
x +5 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
А) 0; |
Б) –5; |
|
|
|
В) –4; |
|
|
|
Г) –9. |
|||||||
1.6.Березы составляют 40 % количества всех деревьев, растущих в парке,
атополя — 30 % количества берез. Сколько процентов количества всех деревьев парка составляют тополя?
А) 20 %; |
Б) 28 %; |
В) 12 %; |
Г) 15 %. |
1.7. Решите уравнение 32x−x2 |
=112x−x2 . |
|
|
А) 0; |
Б) –2; 0; |
В) 0; 2; |
Г) корней нет. |
1.8.Найдите первообразную функции f (x) = sin x , график которой проходит через начало координат.
А) |
F(x) =1−cos x ; |
В) |
F(x) = cos x −1; |
Б) |
F(x) =1+cos x ; |
Г) |
F(x) = −cos x −1. |
1.9. Какое из неравенств выполняется при всех действительных значениях x?
А) (4 x )4 ≤ 0; |
Б) 4 x4 ≥ 0; |
В) 4 x ≥ 0 ; |
Г) (4 x )4 ≥ 0 . |
115
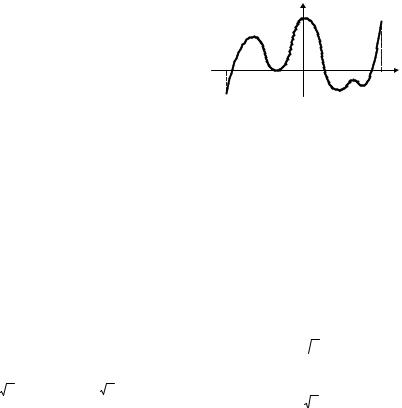
1.10. Функция y = f (x) определена на
промежутке [ a; b] и имеет производную в каждой точке области определения. На рисунке изображен график функции y = f '(x) . Сколько
точек экстремума имеет функция y = f (x)?
y |
|
a |
x |
0 |
b |
А) ни одной точки; |
Б) 6 точек; |
В) 3 точки; |
Г) 4 точки. |
|
1.11. Решите уравнение log2 log2 log3 x = 0 . |
|
|
||
А) 9; |
Б) 8; |
В) 4; |
|
Г) 3. |
1.12. Дважды подбрасывают монету. Какова вероятность того, что герб
выпадет хотя бы один раз? |
|
|
|
|
|
|||||
А) |
2 |
; |
Б) |
1 |
; |
В) |
1 |
; |
Г) |
3 . |
|
3 |
|
|
4 |
|
|
2 |
|
|
4 |
1.13. Стороны параллелограмма пропорциональны числам 3 и 7. Найдите эти стороны, если периметр параллелограмма равен 40 см.
А) 6 см, 14 см; Б) 12 см, 28 см; В) 3 см, 7 см; |
Г) 9 см, 21 см. |
1.14. Катеты прямоугольного треугольника равны 3 см и  7 см. Найдите синус острого угла треугольника, прилежащего к большему катету.
7 см. Найдите синус острого угла треугольника, прилежащего к большему катету.
А) |
7 |
; |
Б) |
7 |
; |
В) |
3 |
; |
Г) |
3 |
. |
|
7 |
||||||||||||
4 |
||||||||||||
4 |
||||||||||||
3 |
1.15. Точка M — середина отрезка AB, не пересекающего плоскость α. Точка A удалена от плоскости α на 6 см, а точка M — на 14 см. Чему равно расстояние от точки B до плоскости α?
А) 18 см; |
Б) 20 см; |
В) 22 см; |
Г) 24 см. |
1.16. Найдите координаты вектора mJG |
= aJG |
|
А) |
JJG |
В) |
m (2; 1; –1); |
||
Б) |
JJG |
Г) |
m (8; 5; 1); |
||
−3bJG , если aG(−1;1;2) , bG(3;2;1) . mJG (10; 5; 1);
mJG (–10; –5; –1).
116
Вариант 50
Часть первая
Задания 1.1 – 1.16 содержат по четыре варианта ответов, из которых только |
|||||||
ОДИН ответ ПРАВИЛЬНЫЙ. Выберите правильный, по Вашему мнению, |
|||||||
|
ответ и отметьте его в бланке ответов. |
||||||
1.1. Какая функция является убывающей? |
|
|
|
||||
А) y = 8x ; |
Б) y = − 8 ; |
В) y = −8x ; |
Г) y = 8x . |
||||
|
x |
|
|
|
|
|
|
1.2. Известно, что 5x :5y =125. Чему равно значение выражения x − y ? |
|||||||
А) 0; |
Б) 1; |
В) 2; |
Г) 3. |
||||
1.3. Найдите значение выражения 6 66 312 . |
|
|
|
||||
А) 54; |
Б) 36; |
В) 18; |
Г) 72. |
||||
1.4. Решите неравенство log2(x − 3) < 3. |
|
|
|
||||
А) (–∞; 11); |
Б) (–∞; 5); |
В) (3; 11); |
Г) (3; 12). |
||||
1.5. Чему равно значение выражения cos2 75°−sin2 75°? |
|
|
|
||||
А) 12 ; |
Б) – 12 ; |
В) |
3 |
; |
Г) – |
3 |
. |
2 |
2 |
||||||
1.6.Укажите множество всех значений x, при которых верно равенство loga x2 = 2loga | x |.
А) (0; +∞); |
|
|
Б) (–∞; 0); |
В) (–∞; 0) (0; +∞); |
|
Г) . |
|
|
|||||||||||
1.7. Решите уравнение sin x − |
|
2 |
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
π |
|
|
|
|
|
|
|
|
|||||||
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
А) (−1)k +1 |
+ πk , k Z ; |
|
|
В) |
± |
+ 2πk , k Z ; |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||
Б) (−1)k |
π |
+ πk , k Z ; |
|
|
Г) |
± 3π + 2πk , k Z . |
|
|
|
|
|
||||||||
4 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|||
|
|
|
|
y |
|
|
|
||||||||||||
1.8. Вычислите площадь заштрихованной фигуры, |
|
|
4 |
|
|
||||||||||||||
|
|
||||||||||||||||||
изображенной на рисунке. |
|
|
|
|
|
|
|
|
|
|
y = |
4− |
x2 |
||||||
А) 16 ; |
|
|
Б) 8 ; |
В) 4; |
|
Г) 6. |
|
|
|
|
|
|
|
||||||
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
1.9. Периодом функции |
y = f (x) является число 5. |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
0 |
|
1 2 |
|
x |
|||||||||||||
Найдите |
значение |
выражения |
2f (−3)+ f (7), |
|
|
|
|
|
|
|
|||||||||
если f (2) = 6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
А) найти невозможно; |
|
Б) 12; |
|
|
|
В) –6; |
|
Г) 18. |
|
|
|||||||||
117
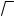
1.10. В арифметической прогрессии ( |
an) известно, что |
a1 = 3, |
a2 = −4. |
||
Укажите формулу n-го члена этой прогрессии. |
|
|
|
||
А) an = 7n −4 ; |
Б) an =10−7n ; |
В) an = −7n −4 ; Г) an = 7n −10 . |
|||
1.11. Среднее арифметическое восьми чисел |
равно |
40, а |
среднее |
||
арифметическое трех из них равно 50. Чему равно среднее |
|||||
арифметическое остальных пяти чисел? |
|
|
|
||
А) 30; |
Б) 35; |
В) 32; |
Г) 34. |
|
|
1.12. В ящике лежат четыре карточки, на которых написаны числа 1, 2, 3 и 5. Какова вероятность того, что произведение чисел, записанных на двух наугад выбранных карточках, является нечетным числом?
А) 1 ; |
Б) |
2 |
; |
В) 1 ; |
Г) |
3 |
. |
|
|||||||
2 |
5 |
|
4 |
4 |
|
||
1.13. Дано: |
∆ABC и ∆MKE, |
A = M, B = K, |
AB = 6 см, BC =12см, |
||||
MK = 3см. Найдите сторону KE. |
|
|
|
||||
А) 8 см; |
Б) 6 см; |
В) 4 см; |
Г) 2 см. |
||||
1.14. Известно, что AD — большее основание трапеции ABCD. Через вершину B проведена прямая, которая параллельна стороне CD и пересекает основание AD в точке M. Найдите периметр трапеции ABCD, если периметр треугольника ABM равен 28 см, а основание BC — 5 см.
А) 28 см; |
Б) 33 см; |
В) 38 см; |
Г) найти невозможно. |
1.15. Вычислите объем пирамиды, основанием которой является парал-
лелограмм со сторонами 4 см и 5 2 см и углом 45° между ними, а высота пирамиды равна 9 см.
2 см и углом 45° между ними, а высота пирамиды равна 9 см.
А) 60 см3; |
Б) 180 см3; |
В) 30 см3; |
Г) 90 см3. |
1.16. Найдите координаты середины отрезка EF, если E(16;7;–8), F(8;–9;–6).
А) (–8; –16; 2); |
В) (12; –1; –7); |
Б) (8; 16; –2); |
Г) (24; –2; –14). |
118

Вариант 51
Часть первая
Задания 1.1 – 1.16 содержат по четыре варианта ответов, из которых только |
||||||||||||||||||||||||||||||
ОДИН ответ ПРАВИЛЬНЫЙ. Выберите правильный, по Вашему мнению, |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
ответ и отметьте его в бланке ответов. |
|
|
|
|
|
|
|||||||||||||||||
1.1. Упростите выражение (1− sinα)(1+ sinα) . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
А) –1; |
|
|
|
|
|
Б) 1; |
|
|
|
В) cos2 α; |
|
|
Г) sin2 α . |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
||||
1.2. Представьте в виде степени выражение b6b2 . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||
А) b 8 ; |
|
|
|
|
|
Б) b |
12 |
; |
|
|
|
В) b |
3 |
; |
|
|
|
|
Г) b 8 . |
|
|
|
||||||||
1.3. Какая функция является степенной? |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
А) y = x8 ; |
|
|
Б) y = 8x ; |
В) y = 8 |
; |
|
|
Г) y = 8x . |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
1.4. Какое из уравнений не имеет корней? |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
А) |
cosx = −π ; |
Б) cosx = − |
π |
; |
В) cosx = − 5 |
; |
Г) cosx = − |
|
3 |
. |
||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|||
1.5. Чему равно значение выражения log4(64a) , если log4 a = 2? |
|
|
|
|||||||||||||||||||||||||||
А) 128; |
|
|
|
|
|
Б) 5; |
|
|
|
В) 66; |
|
|
|
|
Г) 7. |
|
|
|
||||||||||||
1.6. Решите уравнение (14)x (6425)x = (54)2 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
А) 2; |
|
|
|
|
|
Б) 1; |
|
|
|
В) –1; |
|
|
|
|
Г) –2. |
|
|
|
||||||||||||
1.7. Решите неравенство 5log5(3−x) <1. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
А) (2; +∞); |
|
|
Б) (2; 3); |
|
|
|
В) (–∞; 2); |
|
|
Г) (0; 2). |
|
|
|
|||||||||||||||||
1.8. Найдите производную функции |
f (x) = |
x +3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
x −2 |
|
1 |
|
|
|
|
|
|
|
|
||||
А) |
|
f '(x) = |
|
|
|
; |
|
|
|
|
|
В) f '(x) = − |
|
|
|
; |
|
|
|
|
|
|||||||||
|
(x −2)2 |
|
|
|
|
|
(x −2)2 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Б) |
|
f '(x) = |
|
|
5 |
|
; |
|
|
|
|
|
Г) f '(x) = − |
|
5 |
|
|
. |
|
|
|
|
|
|||||||
(x −2)2 |
|
|
|
|
|
(x −2)2 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1.9. Вычислите |
площадь заштрихованной фигуры, |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
y |
|
|
y = 3x |
|||||||||||||||||||||||
изображенной на рисунке. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||||||||
А) |
|
8 |
|
; |
|
|
|
|
|
|
В) |
8ln3; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Б) |
|
3ln3 |
; |
|
|
|
|
|
|
Г) |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3ln310 |
|
|
|
|
|
|
103 ln3. |
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
1 0 |
|
1 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
119

1.10. Найдите номер члена арифметической прогрессии (an ) , равного 10,9,
если a1 = 8,5 и разность прогрессии d = 0,3. |
|
||
А) 7; |
Б) 8; |
В) 9; |
Г) 10. |
1.11. Сколько корней имеет уравнение (x − 4)(x −8) 2− x = 0 ?
2− x = 0 ?
А) один корень; |
В) три корня; |
Б) два корня; |
Г) ни одного корня. |
1.12. Сколько шестизначных чисел, кратных числу 10, все цифры которых различны, можно записать, используя цифры 0, 1, 2, 3, 4 и 5?
А) 36; |
Б) 60; |
В) 24; |
Г) 120. |
1.13.Какое из данных утверждений верно? А) любой ромб является квадратом;
Б) если диагонали четырехугольника перпендикулярны, то он является ромбом;
В) существует квадрат, не являющийся ромбом; Г) если диагонали параллелограмма не равны, то он не является
прямоугольником.
1.14.В окружности, радиус которой равен 13 см, на расстоянии 5 см от центра проведена хорда. Найдите длину этой хорды.
А) 8 см; |
Б) 12 см; |
В) 24 см; |
1.15. На рисунке изображен куб ABCDA1B1C1D1. Укажите угол между прямой AС1 и плоскостью DCС1.
А) C1AD; Б) AC1D; В) AC1C; Г) C1AC.
1.16. При каком положительном значении k модуль |
||
|
JJG |
|
вектора m (2; −3; k) равен 7? |
|
|
А) 36; |
Б) 9; |
В) 8; |
Г) 30 см.
B1 C1 A1 D1
B C A D
Г) 6.
120
