книги / Механика сплошных сред (теоретические основы обработки давлением композитных материалов с задачами и решениями, примерами и упражнениями)

П3. МЕТОДЫ ПОСТРОЕНИЯ КООРДИНАТНЫХ ФУНКЦИЙ

Поясним суть метода на простом примере. Пусть некоторая область Ω имеет

вид прямоугольника. Такую область можно представить в виде пересечения ( ) двух полос, находящихся на интервалах | x | ≤ a и | y | ≤ b соответственно:

Ω = Ω1 Ω2.

Уравнения этих wj полос имеют вид

w1 = a2 – x2 ≥ 0; w2 = b2 – y2 ≥ 0.

Соответственно уравнение границы области Ω определяется соотношением

w = w1 α w2 .

Заменив знак α операции R-конъюнкции его выражением (П3.6) при α= 0, имеем

Формула (П3.9) является аналитическим выражением области Ω, причем функция w положительна внутри этой области, равна нулю на границе и отрицательна вне ее.

Отметим, что метод R-функций наиболее эффективен тогда, когда исследуемая область может быть представлена как комбинация простых областей канонического вида – полуплоскость, полоса, прямоугольник, круг и т. п., – легко поддающихся математическому описанию.

П3.1.3. Метод конформных отображений

Многие задачи МСС могут быть реализованы с использованием в качестве основного решения в (П3.2) так называемых гармонических функций, методам построения которых в произвольных областях на плоскости посвящен раздел математики «Теория функций комплексного переменного» или сокращенно ТФКП. В частности, к таким задачам относятся некоторые задачи «Теории теплопроводности». По предложению Г. Я. Гуна гармонические функции используются для оценки технологических параметров некоторых процессов ОМД и могут быть применены как основное решение с последующей корректировкой по методу М. М. Филоненко-Бородича при моделировании течения металлов в этих процессах. Приведем некоторые необходимые сведения из ТФКП.

Пусть комплексные числа

561

ПРИЛОЖЕНИЕ (МАТЕМАТИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ СПЛОШНЫХ СРЕД)

где i – мнимая единица (i2 = –1) с действительной частью Rez = x1, мнимой

образуют множества Z z и W w соответственно. Геометрически множества Z и W представляют в виде плоскостей, в каждой из которых имеются действительная

ось (x1 – в Z; ϕ – в W) и мнимая ось (x2 – в Z; ψ – в W). Если одному множеству комплексных чисел z из Z ставится в соответствие другое множество комплексных

чисел w из W, то говорят, что задана комплексная функция

комплексного аргумента z. Геометрически функция (П3.12) отображает множество точек z плоскости Z на множество точек w плоскости W. Иначе точка w W называется образом точки z Z. Обратное отображение множества W на множество Z осуществляется с помощью комплексной функции

Если функции (П3.12) и (П3.13) однозначны, то говорят, что они осуществляют взаимно однозначные отображения, а сами функции называются однолист ными. При однолистном отображении функция (П3.13) называется обратной комплексной функцией.

Назначение функции комплексного переменного (П3.12) равносильно заданию двух функций действительных переменных

Комплексная функция w(z) имеет предел w0 = ϕ0 + iψ0 при z → z0 (z0 = a + ib)

lim w = w0 ,

z→z0

если существуют пределы

Функция w(z) называется непрерывной в точке z0, если она определена в некоторой окрестности z0, включая саму точку z0 и

562

П3. МЕТОДЫ ПОСТРОЕНИЯ КООРДИНАТНЫХ ФУНКЦИЙ

lim w( z) = w( z0 ).

z→z0

Для непрерывной в точке z0 = a + ib функции w(z) необходимо и достаточно, чтобы функции ϕ(xi) и ψ(xi) были непрерывными в точках x1 = a; x2 = b.

Функция w(z) называется непрерывной в области D Z, если она непрерывна в каждой точке z D.

Функция w, определенная в некоторой окрестности z точки z, называется

дифференцируемой функцией в точке z, если существует предел

называется производной комплексной функцией по комплексному аргументу. Правила дифференцирования комплексной функции по комплексному аргументу полностью совпадают с таковыми правилами для действительных функций действительного аргумента.

Необходимым и достаточным признаком дифференцируемости функции w(z) в точке (П3.10) является выполнение в этой точке условия Ж. д'Аламбера–Л. Эйлера

Упражнение П3.2. Показать, что функции ϕ и ψ, связанные между собой соотношениями Ж. д'Аламбера–Л. Эйлера (П3.16), являются гармоническими функциями, т. е. удовлетворяющими гармоническим уравнениям П. С. Лапласа

где – дифференциальный оператор (П1.76) 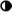Ниже будет показано, что с помощью гармонических функций ϕ и ψ в про-

извольной области D Z можно построить поле скоростей течения идеальной жидкости (мощность внутренних сил в такой жидкости равна нулю). Поля скоростей, построенные на гармонических функциях, будем называть гармоничес кими полями скоростей.

Функция w(z), имеющая производную (П3.15) в точке z D, называется мо ногенной в этой точке. Если однозначная функция w(z) моногенна в каждой точ-

563

ПРИЛОЖЕНИЕ (МАТЕМАТИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ СПЛОШНЫХ СРЕД)

ке z D, то она называется аналитической (регулярной) во всей области D. Производная (П3.15) аналитической функции представима в следующих равносильных формах:

которые учитывают условие (П3.16).

В соответствии с теоремой О. Коши всякая аналитическая в области D функция f(z) в окрестности точки z0 D может быть разложена в ряд Б. Тейлора

радиус сходимости которого меньше, чем расстояние от z0 до границы области

Тогда аналитическая в открытой окрестности (круговой области) с центром в точке z0 функция f(z) может быть представлена в виде степенного ряда

Функция аналитическая в кольцевых незамкнутых областях r < || z – z0 || < R (r ≥ 0; R ≤ ∞) может быть разложена в ряд А. П. Лорана

ω– окружность радиуса δ = || ζ – z0 ||, r < δ < R.

Всвязи с тем, что аналитические функции многократно дифференцируемы, функцию f(z) можно представить в виде производной некоторой аналитической функции w(z)

f(z) = w′(z).

Наоборот, w(z) определяется с точностью до аддитивной постоянной через функцию f(z):

564

П3. МЕТОДЫ ПОСТРОЕНИЯ КООРДИНАТНЫХ ФУНКЦИЙ

w( z) = ∫ f ( z)d z.

z

Используя разложения (П3.19) и (П3.20), получим представление функции w(z) в виде

Введем обозначения: k = – m; ak = C– m. Тогда ряд (П3.21) может быть представлен в следующей форме:

В этом ряду каждое слагаемое

является аналитической функцией во всех точках, кроме z = z0. Такие слагаемые будем называть простейшими аналитическими функциями. Точка z0 называется изолированной особой точкой функции w(z), если существует окрестность 0 < || z – z0 || < R этой точки (с исключением z0), в которой w(z) аналитична. Различают три типа изолированных особых точек, в зависимости от поведения функции w(z) в их окрестности:

а) точка z0 называется устранимой особой точкой, если существует конеч-

ный предел lim w(z) ;

z→z0

б) точка z называется полюсом, если lim w(z) = ∞ ;

0 z→z0

в) точка z0 называется существенно особой точкой, если не существует

lim w(z) .

z→z0

Функция w(z) называется целой (голоморфной) в некоторой области D, если в этой области она не имеет особых точек. Функция w(z) называется дробной (ме роморфной) в области D, если в этой области она не имеет других особенностей, кроме полюсов.

565

ПРИЛОЖЕНИЕ (МАТЕМАТИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ СПЛОШНЫХ СРЕД)

Нулем функции w(z) называют любую точку z = z0, в которой w(z0) = 0. Аналитическая функция w(z) в области своего существования может иметь лишь счетное множество нулей (предполагается, что во всей области не выполняется условие w(z) ≡ 0). В области аналитичности, в окрестности своего нуля z0 функция w(z) разлагается в ряд

где n ≥ 1. Число n называется порядком, или кратностью нуля. При n = 1 точка z0

называется простым нулем.

Целая функция w(z) может быть представлена в виде бесконечного произведения

где p – наименьшее неотрицательное число, для которого

h(z) – целая функция (полином степени не выше p); zk – последовательность нулей w(z), в которую каждый нуль входит столько раз, какова его кратность.

Приведем примеры представления целых функций в виде бесконечного произведения:

В ТФКП показано, что с помощью аналитических функций в некоторой области D Z, ограниченной линиями ϕ= ϕ+ = const; ϕ= ϕ– = const; ψ = ψ+ = const;

ψ= ψ– = const, можно построить плоское гармоническое поле скоростей. Рассмотрим плоское векторное поле

которое должно удовлетворять условиям соленоидальности

566

П3. МЕТОДЫ ПОСТРОЕНИЯ КООРДИНАТНЫХ ФУНКЦИЙ

Легко показать, что такое векторное поле может быть определено с помощью гармонических скалярных функций. Иначе одновременно соленоидальное и потенциальное векторные поля являются гармоническими. Действительно, для тождественного удовлетворения условию (П3.25) удобно ввести некоторую скалярную функцию ψ, называемую функцией тока, такую, что

При подстановке компонент (П3.27) вектора V в условие (П3.25) последнее обращается в тождество. Кроме того, для обращения в тождество условия (П3.26) удобно ввести другую скалярную функцию ϕ, называемую потенциалом векто ра скорости, или консервативной функцией, такую, что

При этом подстановка (П3.28) в (П3.26) также обращает последнее в тождество. Упражнение П3.3. Доказать, что подстановка (П3.27) в (П3.26) и (П3.28) в (П3.25) приводит к уравнениям П. С. Лапласа (П3.17), а подстановка (П3.27) в

(П3.25) и (П3.28) в (П3.26) – к тождеству Сравнивая (П3.27) и (П3.28) с условием Ж. д'Аламбера – Л. Эйлера (П3.16) и

с производной аналитической функции w(z) по комплексному аргументу z (П3.18), устанавливаем, что построение гармонического плоского векторного поля может быть сведено к построению аналитической функции (П3.11), назы-

ваемой для поля v комплексным потенциалом. Иначе, искомый вектор v (П3.24) будет равен величине, комплексно сопряженной с первой производной комплексного потенциала по комплексному аргументу z:

Величина w′называется комплексной скоростью. Производная комплексной скорости w′(z) по аргументу z может быть представлена в следующих равносильных формах:

567

ПРИЛОЖЕНИЕ (МАТЕМАТИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ СПЛОШНЫХ СРЕД)

Величина w′′ называется комплексной скоростью деформации.

С помощью гармонического векторного поля (П3.24), удовлетворяющего условиям (П3.25) и (П3.26), можно описать поле скоростей течения идеальной жидкости в некоторой области D, принадлежащей плоскости Z. Такую плоскость будем называть физической плоскостью, а построенные в D течения – гар моническими течениями. Линии тока (векторные линии поля скоростей) такого течения будут характеризоваться функцией тока

называемые эквипотенциальными линиями, вместе с линиями тока в плоскости Z образуют ортогональную сетку.

В ТФКП часто используется принцип отвердения, согласно которому любая линия тока (П3.31) течения с соленоидальным полем скоростей (П3.25) может рассматриваться как граничная линия некоторой области такого течения.

Комплексный потенциал (П3.10) осуществляет конформное отображение области D физической плоскости Z на область E (полоса, полуполоса или прямоугольник) плоскости комплексного потенциала W. При таком отображении угол между двумя любыми линиями в плоскости Z равен углу между образами этих линий в плоскости W, а бесконечно малые окружности в плоскости Z с точностью до малых высшего порядка остаются окружностями в плоскости W.

Таким образом, в ТФКП, по существу, разработаны методы конформного отображения произвольной области D, ограниченной эквипотенциалами ϕ = ϕ+; ϕ = ϕ– и линиями тока ψ = ψ+; ψ = ψ–, в плоскости физического течения Z на прямоугольник E, ограниченный прямыми линиями ϕ+ = const; ϕ– = const и ψ+ = const; ψ– = const в плоскости комплексного потенциала W.

П3.1.4. Метод интеграла К. Шварца–Э. Кристоффеля

Для конформного отображения полигональной области D, представляющей собой n-угольник с вершинами Ak и суммой внутренних углов α, выраженных в долях π

568

П3. МЕТОДЫ ПОСТРОЕНИЯ КООРДИНАТНЫХ ФУНКЦИЙ

k=1

ипостроения в этой области комплексного потенциала (П3.10) применяется

метод интеграла К. Шварца–Э. Кристоффеля.

Всоответствии с этим методом комплексный потенциал (П3.10) записывается в параметрическом виде

где функции z и w комплексного аргумента ζ записываются с помощью интеграла К. Шварца–Э. Кристоффеля:

Областью изменения комплексного параметра ζ = ξ + iη является верхняя полуплоскость (η ≥ 0) вспомогательной плоскости ζ. Таким образом, интеграл К. Шварца–Э. Кристоффеля позволяет конформно отобразить область D физической плоскости Z и область Е плоскости комплексного потенциала W на полуплоскость вспомогательной плоскости ζ.

Величины ak и bj в (П3.35) называются константами интеграла К. Шварца– Э. Кристоффеля. Они являются образами вершин Ak области D и Bj области E на действительной оси ξ соответственно. Принято положительным обходом облас ти считать такое движение вдоль ее границы, при котором область обхода остается слева. Назначение констант ak и bj на оси ξ и вершин Bk в области E, являющихся образами вершин Ak в области D, должно быть таким, чтобы при положительном обходе области D в Z и ее образов, как на границе прямоугольника E в W, так и на границе верхней полуплоскости в ζ, последовательность точек Ak соответствовала последовательности всех встречаемых их образов.

Главную трудность применения интеграла К. Шварца–Э. Кристоффеля составляет определение неизвестных констант ak (bj). Частично эта трудность устраняется за счет одного из свойств интеграла: при его составлении три любые его константы из множества ak (из множества bj) можно назначать произвольно (свобода выбора), а остальные константы ak (bj) и постоянные Cm должны быть определены из условий задачи или в процессе ее решения. Однако следует от-

569

ПРИЛОЖЕНИЕ (МАТЕМАТИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ СПЛОШНЫХ СРЕД)

метить, что свобода выбора трех констант ak (bj) всегда определяется необходи мостью решения задачи, так как неудачный выбор их может привести к сложному подынтегральному выражению в (П3.35). При назначении констант обычно используют еще одно свойство интеграла К. Шварца–Э. Кристоффеля: если одна констант ak (bj) помещена в бесконечность, то соответствующий этой константе в интеграле (П3.35) сомножитель равен единице. Процедура назначения трех произвольных констант называется нормировкой интеграла К. Шварца–

Э. Кристоффеля.

Значения нижних пределов интегрирования ζ0 в (П3.35) связано с выбором множества координат в плоскостях z, W и ζ.

Упражнение П3.4. Используя метод интеграла К. Шварца–Э. Кристоффеля и его нормировки для физической плоскости Z и плоскости комплексного потенциала W

показать, что конформному отображению области D, ограниченной в плоскости Z двумя лучами ψ+ = const и ψ– = const, исходящими из начала координат с углом α между ними, на полосу E шириной Δψ = ψ+ – ψ– в плоскости W соответствует комплексный потенциал

Покажем, что аналитическая функция (П3.36) описывает в физической плоскости Z течение потока источника при Δψ > 0 (стока при Δψ < 0) с интенсивностью (мощностью, производительностью) Δψ, помещенного в начало координат. Для этого разложим комплексный потенциал (П3.36) на действительную ϕ

имнимую ψ части (П3.11) при ImС1 = 0:

ϕ= Δψ ln (x2 + x2 )+ln α ; ψ = Δψ arctg x2 .

πα 1 2 C1 πα x1

Введем обозначения:

570