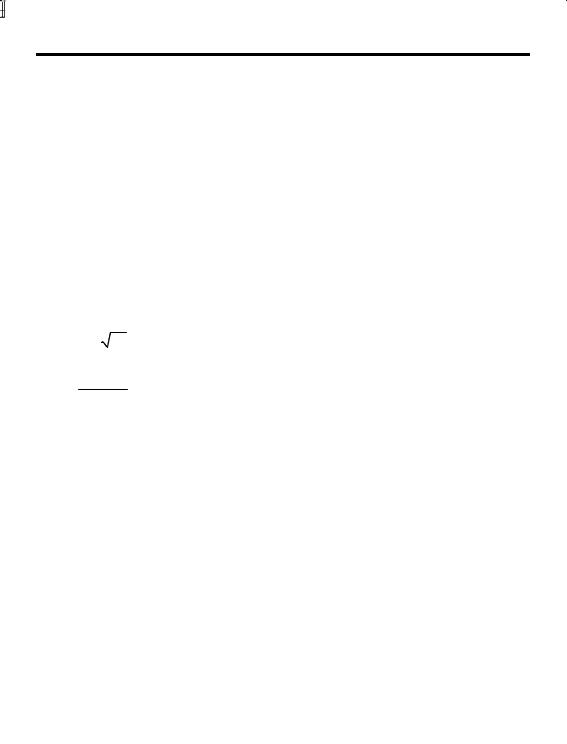книги / Механика сплошных сред (теоретические основы обработки давлением композитных материалов с задачами и решениями, примерами и упражнениями)

П1.9. Основные интегральные зависимости

Рассмотрим некоторые обобщения интегральных операций над векторами из векторного анализа для тензоров произвольного ранга.

Пусть область : ограничена поверхностью S с единичной внешней норма-

лью n . В дальнейшем предполагается, что S удовлетворяет всем требованиям, предъявляемым к поверхностям при выводе формул стоксовского типа векторного анализа. Тогда справедливо обобщение этих формул для тензоров произвольного ранга.

Если – замкнутый контур, каждая точка которого характеризуется радиу-

сом-вектором x , то в соответствии с обобщением формулы Дж. Стокса цирку

512

П1. ЭЛЕМЕНТЫ МАТРИЧНОГО И ТЕНЗОРНОГО ИСЧИСЛЕНИЙ

k

ляция тензорного поля Τa по контуру равна потоку ротора этого поля через

поверхность S , натянутую на контур , т. е.

В частности, если в (П1.100) k = 2 и Ta = Tb × , то, учитывая, что для симметричного тензора Tb

В соответствии с обобщением формулы М. В. Остроградского–К. Гаусса по-

k

ток поля Τa через замкнутую поверхность S с единичной внешней нормалью n

k

равен интегралу от дивергенции поля Τa по области Ω, ограниченной этой поверхностью, т. е.

SΩ

ВМДТТ неоднократно рассматривается задача об определении некоторого вектора a по заданной симметричной части

производной вектора по векторному аргументу a (П1.83). В этом случае получается переопределенная задача о нахождении трех (в трехмерном пространстве) компонент вектора a из шести скалярных уравнений. Если бы значения компонент тензора a = Τb + Τc , где

513

ПРИЛОЖЕНИЕ (МАТЕМАТИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ СПЛОШНЫХ СРЕД)

является альтернативной частью (П1.51) тензора a , были нам известны, то можно бы найти значение a по формуле

x

a = a0 + ∫ (a ) dy,

x0

где a0 – значение вектора a в точке m0 начала пути интегрирования с радиу- сом-вектором x0 . В этой формуле заменим подынтегральное выражение суммой его симметричной Tb (П1.104) и альтернативной Tc (П1.105) частей. Тогда

x x

a = a0 + ∫ Τb dy + ∫ Τc dy.

x0 x0

Перепишем последнее слагаемое этого выражения, используя значение Tc (П1.105) и тождество (П1.86)

а затем выполним интегрирование последнего слагаемого по частям:

С помощью (П1.86) третье слагаемое правой части (П1.106) запишем через значение Τc0 тензора Tc (П1.105) в точке m0: Τc0 ( x− x0 ) = 0,5( × a)×(x− x0 ) , а в

Тогда окончательно получаем формулу для вычисления вектора a по заданной симметричной части Tb производной этого вектора по векторному аргументу:

514

П1. ЭЛЕМЕНТЫ МАТРИЧНОГО И ТЕНЗОРНОГО ИСЧИСЛЕНИЙ

x0 x0

Скалярная форма записи формулы (П1.108) в декартовом прямолинейном множестве координат известна как формула Е. Чезаро.

Контрольные вопросы

1.Как формулируется правило А. Эйнштейна и исключение А. И. Лурье из этого правила?

2.Какие численные значения и в каких случаях принимают символы Л. Кронекера и Т. Леви-Чивиты?

3.Как записываются свойства матрицы косинусов по ее строкам и столбцам, с помощью которой осуществляется поворот декартова множества координат?

4.Что называется ортом?

5.Что называется декартовым тензором ранга (валентности) n в N-мерном пространстве? Как связаны с определением тензора скалярные и векторные величины?

6.В чем принципиальное отличие тензора второго ранга с компонентами аik от определителя и матрицы с такими же компонентами?

7.Как осуществляется р-скалярное произведение тензоров различного ранга. В каких случаях это произведение называется полным скалярным, а в каких – тензорным?

8.Как выполняется р-векторное произведение тензоров различного ранга и когда оно становится полным векторным?

9.Как выполняются операции транспонирования, симметрирования и альтернирования тензора? Как связаны между собой компоненты симметричного тензора, кососимметричного тензора?

10.Какие характеристики тензора зависят от ориентации множества координат и какие не изменяются при его повороте?

11.Что называется главным направлением тензора, главным множеством координат тензора?

12.Какой вид имеет матрица тензора в главном множестве координат и как определяются главные компоненты тензора?

13.Приведите примеры физических и геометрических аналогов тензоров нулевого, первого, второго, третьего и четвертого рангов; почему разность между тензором и его девиатором называется сферической частью тензора?

515

ПРИЛОЖЕНИЕ (МАТЕМАТИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ СПЛОШНЫХ СРЕД)

14.Что называется тензорным полем и в каких случаях тензорные поля являются нестационарными? Как математически записывается условие стационарности тензорных полей?

15.Как образуется дифференциальный оператор В. Р. Гамильтона (набла) произвольного ранга n?

16.Как выполняются над тензором дифференциальные операции различного ранга градиент, дивергенция и ротор? Как вычисляется производная тензора по векторному аргументу?

17.Приведите примеры множеств координат, в которых полная и частная производные тензора по координатам совпадают и различаются; как вычисляется полная производная в последнем случае?

18.Как записывается обобщение формулы М. В. Остроградского–К. Гаусса?

19.Каким образом вычисляется вектор по симметричной части его градиента?

Типовые варианты контрольной работы № 1 по разделу МСС «Тензорное исчисление и анализ тензорных полей»

Иллюстративный вариант А. С чем связано название сферической части тензора второго ранга?

Б. Какие оси координат называются главными осями тензора?

значение c = a Τb ; скалярное произведение a и c ; векторное произведение c и a ; тензорное произведение a и c .

Г. Записать матрицу тензора Тb из п. B в главных координатах.

Д.По векторному полю v с компонентами v1 = x13 − x23 ; v2 = x1 x22 в точке с

координатами x1 = 1; x2 = –1 найти один из единичных векторов n , направленный по касательной к изолинии скалярного поля ϕ = v .

Е. Расписать в скалярной форме ( u ) .

516

П1. ЭЛЕМЕНТЫ МАТРИЧНОГО И ТЕНЗОРНОГО ИСЧИСЛЕНИЙ

Ответы по пунктам иллюстративного варианта А. Название связано с геометрическим аналогом этой части тензора – сферой.

Б. Оси координат, которые совпадают с главными направлениями тензора.

∂2 u j

Е.∂ xk ∂ xj .

Вариант 1

А.Как формулируется правило А. Эйнштейна для повторяющихся индексов в одночлене, содержащем индексированные переменные?

Б. Как определяется производная вектора по векторному аргументу?

лить: значение c = Τb a ; скалярное произведение a и c ; векторное произведение c и a ; тензорное произведение a и c .

Г. Записать матрицу тензора Тb из п. B в главных координатах.

Д.По векторному полю v с компонентами v1 = x12 + x22 ; v2 = x12 x2 в точке с

координатами x1 = 1; x2 = 2 найти один из единичных векторов n , направленный по касательной к изолинии скалярного поля ϕ = v .

Е. Расписать в скалярной форме ×( ×u ) .

517

ПРИЛОЖЕНИЕ (МАТЕМАТИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ СПЛОШНЫХ СРЕД)

Вариант 2 А. Какие векторы называются ортами?

Б.Какому закону должны удовлетворять компоненты αkj строк матрицы косинусов?

лить: значение c = a Τb ; скалярное произведение a и c ; векторное произведение c и a ; тензорное произведение c и a .

Г. Записать матрицу тензора Тb из п. B в главных координатах.

Д. По скалярному полю ϕ = x12 x23 в точке с координатами x1 = 2; x2 = 3 найти один из единичных векторов n , ортогональный вектору v = ϕ.

Е. Расписать в скалярной форме ×( Τa ) .

Вариант 3 А. Какие операции можно выполнять над матрицами?

Б. Чему равен первый инвариант девиатора?

значение c = Τb a ; скалярное произведение a и c ; векторное произведение c и a ; тензорное произведение a и c .

Г. Записать матрицу тензора Тb из п. B в главных координатах.

Д. По векторному полю v с компонентами v1 = x1 x22 x3 ; v2 = x12 x2 x3 в точке с координатами x1 = 1; x2 = 3; x3 = 2 найти один из единичных векторов n , ортогональный вектору u = v .

Е. Расписать в скалярной форме ( u ) .

Вариант 4 А. Как формулируется исключение А. И. Лурье из правила А. Эйнштейна?

518

П1. ЭЛЕМЕНТЫ МАТРИЧНОГО И ТЕНЗОРНОГО ИСЧИСЛЕНИЙ

лить: значение c = a Τb ; скалярное произведение a и c ; векторное произведение c и a ; тензорное произведение c и a .

Г. Записать матрицу тензора Тb из п. B в главных координатах.

x2 = 3 найти один из единичных векторов n , ортогональный вектору

u= Τa .

Е.Расписать в скалярной форме ( u ) .

Вариант 5 А. Каким условиям должны удовлетворять перемножаемые матрицы?

Б. Как вычисляются величины aI, aII, aIII тензора Тa = [[aik]]?

числить: значение c = Τb a ; скалярное произведение a и c ; векторное произведение c и a ; тензорное произведение a и c .

Г. Записать матрицу тензора Тb из п. B в главных координатах.

Д.По векторному полю v с компонентами v1 = x1 x23 ; v2 = x14 + 2 x24 в точке с

координатами x1 = 1; x2 = –2 найти один из единичных векторов n , направленный по касательной к изолинии скалярного поля ϕ = v .

Е. Расписать в скалярной форме 2 Τa .

Вариант 6 А. Что называется скаляром?

519

ПРИЛОЖЕНИЕ (МАТЕМАТИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ СПЛОШНЫХ СРЕД)

Б. Какие компоненты тензора называются главными?

лить: значение c = a Τb ; скалярное произведение a и c ; векторное произведение a и c ; тензорное произведение c и a .

Г. Записать матрицу тензора Тb из п. B в главных координатах.

Д.По скалярному полю ϕ = x13 x23 в точке с координатами x1 = –1; x2 = 3 найти единичный вектор n , совпадающий по направлению с вектором

v= ϕ.

Е. Расписать в скалярной форме (u ) .

Вариант 7 А. Что называется главным направлением тензора?

Б.Какому закону должны удовлетворять компоненты αkj столбцов матрицы косинусов?

лить: значение c = Τb a ; скалярное произведение a и c ; векторное произведение c и a ; тензорное произведение a и c .

Г. Записать матрицу тензора Тb из п. B в главных координатах.

Д.По векторному полю v с компонентами v1 = x14 x23 ; v2 = x12 x25 в точке с

координатами x1 = –1; x2 = –2 найти единичный вектор n , совпадающий по направлению с вектором u = 2 v .

Е. Расписать в скалярной форме ψ .

Вариант 8

А.По какой схеме выполняется р-скалярное произведение и в каком случае оно называется полным скалярным произведением?

520