П1. ЭЛЕМЕНТЫ МАТРИЧНОГО И ТЕНЗОРНОГО ИСЧИСЛЕНИЙ
или
xi = αk i xk′ .
Тогда
∂x′i = αk i .
∂xk
Рассмотрим производные компонент вектора a в новом базисе по новым координатам:
∂ai′ |
∂ xm |
= αkp |
∂ai′ |
. |
|
|
∂ xm ∂ xk′ |
|
∂ xp |
При переходе к новому множеству координат ai′ = αiq aq . Тогда
∂a′ |
|
∂aq |
|
i |
= αkpαiq |
|
|
, |
∂ x |
∂ x |
p |
k |
|
|
|
а это и есть закон (П1.27), записанный для преобразования компонент тензора второго ранга.
Примечание. Поскольку дифференциал каждой компоненты вектора a
|
d a |
= |
∂ai |
d x |
, |
|
|
|
|
∂ x |
|
|
|
|
|
i |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
то дифференциал вектора a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ap |
|
|
|
|
|
∂a |
|
d x |
|
d a = d a e |
= |
|
|
d x e |
|
= |
m |
|
∂ x |
|
|
|
i i |
|
k |
|
k |
|
p |
|
∂ x |
j |
|
j |
|
|
|
|
|
|
|
|
|
|
|
или
ПРИЛОЖЕНИЕ (МАТЕМАТИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ СПЛОШНЫХ СРЕД)
Иначе, полная производная вектора по векторному аргументу образует тензор второго ранга:
Тензор с транспонированной матрицей называется градиентом вектора
Задача П1.8.1.3. В точке М(1, 2, 3) вычислить полную производную вектора a = x1 x2 e1 + x2 x3 e2 + x3 x1 e3 по вектору x , градиент этого вектора и след матриц полученных тензоров.
Решение. По формуле (П1.8.13) проводим вычисление полной производной вектора по векторному аргументу
|
d a |
= |
x2 |
x1 |
0 |
|
0 |
x |
x |
|
|
|
|
d x |
|
|
3 |
2 |
|
|
x3 |
0 |
x1 |
|
|
|
|
|
или в точке М |
|
|
|
|
|
|
d a |
|
2 |
1 |
0 |
|
|
= |
0 |
3 |
2 . |
|
|
d x |
|
|
|
3 |
0 |
1 |
|
|
|
|
|
Матрицу градиента вектора a можем получить транспонированием предыдущей матрицы
x2 |
0 |
x3 |
a = x1 |
x3 |
0 |
0 |
x2 |
x1 |
или в точке М

П1. ЭЛЕМЕНТЫ МАТРИЧНОГО И ТЕНЗОРНОГО ИСЧИСЛЕНИЙ
2 0 3a = 1 3 0 .
0 2 1
Отметим, что след матрицы обоих полученных тензоров равен дивергенции вектора a :
a = ∂ at .
∂xi
Спомощью числовых значений компонент матриц тензоров получим
a = 2 + 3 +1 = 6.
Задача П1.8.1.4. Показать, что альтернативная часть полной производной вектора a по векторному аргументу x связана с вихрем векторного поля a .
Решение. Разложим полную производную вектора a по векторному аргументу задачи П1.8.1.2 на симметричную и альтернативную части. Разложение, используя дифференциал вектора a , представим в виде
|
d a = |
1 |
|
∂ ai |
+ |
∂ ak |
d x+ |
1 |
|
∂ ai |
− |
∂ ak |
d x. |
|
2 |
∂ x |
2 |
∂ x |
|
|
|
|
∂ x |
|
|
|
∂ x |
|
|
|
|
|
k |
|
i |
|
|
|
k |
|
i |
|
Здесь второе слагаемое полного дифференциала d a есть произведение антисимметричной части полной производной вектора a по векторному аргументу
на дифференциал d x . Обозначим это произведение через d b и распишем его с цифровыми индексами:
|
|
|
|
1 |
|
∂ a |
∂ a |
|
|
|
|
|
|
|
∂ a |
|
∂ a |
|
|
|
|
|
|
|
d b = |
|
|
|
|
|
|
|
1 |
|
− |
|
|
|
2 |
|
d x |
+ |
|
|
|
1 |
|
− |
|
|
3 |
|
|
d x |
|
e + |
2 |
|
∂ x |
|
|
|
|
∂ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ x |
|
|
|
2 |
|
|
∂ x |
|
|
|
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
3 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
1 |
∂ a |
|
− |
∂ a |
|
|
|
|
|
+ |
∂ a |
|
− |
∂ a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3 |
|
d x |
|
|
|
|
2 |
|
1 |
|
|
d x |
|
e + |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
∂ x |
|
|
∂ x |
|
|
3 |
|
∂ x |
|
|
∂ x |
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
1 ∂ a |
− |
|
∂ a |
|
|
d x + |
∂ a |
− |
∂ a |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
1 |
|
|
|
|
|
3 |
|
|
|
d x |
|
|
e . |
|
|
|
|
|
|
|
|
|
∂ x |
|
∂ x |
|
|
|
|
|
|
|
2 ∂ x |
|
|
|
|
|
|
1 |
|
|
∂ x |
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ПРИЛОЖЕНИЕ (МАТЕМАТИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ СПЛОШНЫХ СРЕД)
Теперь рассмотрим векторное произведение
d c = ( a) d x.
Компоненты промежуточного вектора (ротора вектора a )
d = × a
записываются с помощью символа Т. Леви-Чивиты (П1.4)
Тогда компоненты вектора d c = d× d x найдем как векторное произведение
d c |
= |
|
∂ am d x . |
i |
ijk |
j |
m ∂ x k |
Расписывая последнее соотношение по цифровым индексам, учитывая свойства символа Т. Леви-Чивиты (П1.4), получим
|
|
|
∂ a |
|
∂ a |
|
|
|
|
|
|
∂ a |
∂ a |
2 |
|
|
|
d c = |
|
|
|
1 |
|
− |
|
3 |
|
d x |
+ |
|
|
|
1 |
|
− |
|
|
|
|
d |
∂ x |
∂ x |
∂ x |
∂ x |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
∂ a |
|
− |
∂ a |
|
|
|
+ |
∂ a |
2 |
− |
|
∂ a |
|
|
|
|
|
|
|
2 |
|
1 |
|
d x |
|
|
|
|
|
|
3 |
|
|
d x |
|
|
∂ x |
|
|
∂ x |
|
∂ x |
|
|
∂ x |
|
|
|
1 |
|
|
|
|
|
3 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
∂ a |
− |
∂ a |
|
|
|
|
+ |
∂ a |
− |
∂ a |
|
|
|
|
|
3 |
|
2 |
|
d x |
|
|
3 |
1 |
|
d x |
|
e . |
|
|
∂ x |
|
∂ x |
|
∂ x |
|
2 |
|
∂ x |
|
1 |
3 |
|
|
2 |
|
|
3 |
|
|
|
|
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сравнивая компоненты векторов d b и d c , устанавливаем, что
|
∂ ai |
− |
∂ ak |
d x = ( a) d x. |
|
∂ x |
|
|
∂ x |
|
|
k |
|
i |
|
Задача П1.8.1.5. Показать, что ротор второго ранга градиента вектора b равен нулю.

П1. ЭЛЕМЕНТЫ МАТРИЧНОГО И ТЕНЗОРНОГО ИСЧИСЛЕНИЙ
Решение. Градиент вектора b обозначим тензором
Τa = b ,
компоненты которого a |
= |
∂bk . |
|
|
|
|
|
i k |
|
∂ x |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
Тогда ротор второго ранга такого тензора |
|
|
|
|
|
2 Ta = [[rmp]] |
имеет компоненты |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
∂2 a |
|
|
r |
|
|
i k |
. |
|
|
pqk ∂ x |
|
|
|
mp |
mji |
|
∂ x |
|
|
|
|
|
|
i |
q |
Теперь вместо компонент aik подставим соответствующие значения компонент градиента вектора b и покажем, что полученный результат тождественно равен нулю:
rmp = mji pqk |
|
∂3 b |
|
|
|
|
k |
|
≡ 0. |
∂ x |
j |
∂ x |
∂ x |
|
|
q |
i |
Действительно, учитывая, что индексы j и i принадлежат одному и тому же символу Т. Леви-Чивиты, а также производится дифференцирование по аргументам xj и xi с такими же индексами, устанавливаем:
1)замена отличных друг от друга цифровых значений индексов j и i местами изменит знак символа Т. Леви-Чивиты на противоположный;
2)такая же замена не повлияет на порядок дифференцирования по аргу-
ментам xj и xi.
На основании изложенного, при суммировании по повторяющимся индексам j и i эта сумма будет состоять из нескольких пар одинаковых слагаемых, отличающихся знаком. Поэтому сама сумма будет тождественно равна нулю.
Окончательно
2 ( b ) ≡ 0.
Самостоятельно. Доказать следующее тождество
2 × dd bx ≡ 0.

ПРИЛОЖЕНИЕ (МАТЕМАТИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ СПЛОШНЫХ СРЕД)
Задача П1.8.1.6. Показать, что при векторном умножении тензорного оператора набла второго ранга на симметричную Tb и кососимметричную Tc части потенциального тензора Ta получаются нулевые тензоры.
Решение. Потенциальность тензора Ta второго ранга
2 Ta = 0
предполагает существование такого вектора d , что тензор равен градиенту этого вектора:
Τa = d .
Вэтом случае компоненты тензора
aqm = ∂dm .
∂ xq
Тогда условие потенциальности обращается в тождество:
ijq kp m |
|
∂3 dm |
|
≡ 0. |
∂ x |
j |
∂ x |
p |
∂ x |
|
|
|
|
|
q |
Самостоятельно непосредственным расписыванием последнего тождества по цифровым индексам убедиться в его выполнении.
Транспонированный тензор Τaт исходного тензора имеет компоненты
am q = ∂dm ,
∂ xq
и подстановка их в условие потенциальности вместо компонент исходного тензора не внесет существенной поправки в это условие:
ij m kpq |
|
∂3 dm |
≡ 0. |
∂ x |
j |
∂ x |
p |
∂ x |
|
|
|
q |
|
Таким образом, транспонированный тензор потенциального тензора также является потенциальным. Тогда для симметричной части исходного тензора получаем

П1. ЭЛЕМЕНТЫ МАТРИЧНОГО И ТЕНЗОРНОГО ИСЧИСЛЕНИЙ
|
∂2 bmq |
= |
1 |
|
|
∂2 |
∂dv + |
∂dt |
≡ 0 |
|
|
fuv |
|
|
ijq kpm |
∂ xj ∂ xp |
|
2 |
srt |
|
∂ xt |
|
|
|
|
|
|
∂ xj ∂ xp |
∂ xv |
|
и для альтернативной части имеем
|
∂2 cm q |
= |
1 |
|
|
∂2 |
∂dv − |
∂dt |
≡ 0. |
|
|
fuv |
|
|
ijq kp m |
∂ xj ∂ xp |
|
2 |
srt |
|
∂ xt |
|
|
|
|
|
|
∂ xj ∂ xp |
∂ xv |
|
Окончательно для потенциального тензора Ta его симметричная Tb и альтернативная Tc части также потенциальны:
2 × Tb ≡ 0; 2 × Tc ≡ 0.
П1.8.2. Дифференцирование тензорных полей по времени
Задача П1.8.2.1. По заданному тензору
|
|
|
t x |
x |
0 |
|
t x |
2 |
|
|
|
2 |
3 |
|
|
1 |
Τ |
a |
= |
t x |
2 |
t x |
x |
0 |
|
|
|
1 |
2 |
3 |
|
|
|
|
|
0 |
|
t x |
2 |
t x |
x |
|
|
|
|
|
1 |
2 |
3 |
определить его частную производную по времени, когда все координаты xi являются линейно независимыми и не зависят от времени t.
Решение. Для решения этой задачи необходимо найти частную производную по времени t от всех компонент заданного тензора:
x |
|
x |
0 |
x2 |
2 |
|
3 |
|
|
|
1 |
∂Τa = |
x2 |
|
x |
x |
0 . |
∂t |
|
1 |
|
2 |
3 |
|
|
0 |
|
x2 |
x |
x |
|
|
|
|
|
|
|
1 |
2 |
3 |
Задача П1.8.2.2. По тензору, заданному в предыдущей задаче, определить его полную производную по времени t, когда все координаты xi также линейно независимы, но все они зависят от времени xi = ait, где величины ai являются константами.

ПРИЛОЖЕНИЕ (МАТЕМАТИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ СПЛОШНЫХ СРЕД)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
15 |
−21 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−9 |
|
|
|
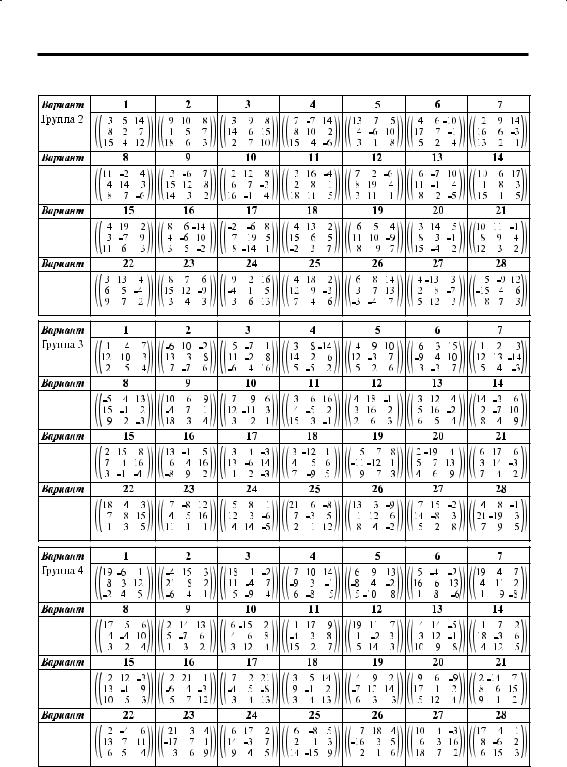
Пункт |
Б |
ДЗ |
№ |
1. |
По |
|
|
матрицам |
M p = |
2 |
8 |
10 |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
0 |
16 |
−6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
8 |
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
5 |
6 |
−8 10 |
|
|
|
|
|
6 |
4 16 1 |
|
|
|
|
|
|
|
|
|
|
−2 |
|
|
|
M f = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mq = |
12 |
4 |
9 |
|
, |
|
|
2 |
10 |
0 |
1 |
|
и схеме их произведения |
|
1 |
−15 |
7 |
2 |
|
|
|
|
|
2 |
−9 |
27 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
−8 19 3 |
|
|
|
|
|
|
|
|
|
4 13 16 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
определить указанные компоненты матрицы Mg = ((gij)).
Варианты по пункту Б ДЗ № 1
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
Группа 1 |
g11 |
g12 |
g13 |
g14 |
g11 |
g12 |
g13 |
g14 |
g11 |
g12 |
g13 |
g14 |
g11 |
g12 |
g13 |
g14 |
Группа 2 |
g21 |
g22 |
g23 |
g24 |
g11 |
g12 |
g13 |
g14 |
g11 |
g12 |
g13 |
g14 |
g11 |
g12 |
g13 |
g14 |
Группа 3 |
g31 |
g32 |
g33 |
g34 |
g11 |
g12 |
g13 |
g14 |
g11 |
g12 |
g13 |
g14 |
g11 |
g12 |
g13 |
g14 |
Группа 4 |
g41 |
g42 |
g43 |
g44 |
g11 |
g12 |
g13 |
g14 |
g11 |
g12 |
g13 |
g14 |
g11 |
g12 |
g13 |
g14 |
Схема |
gik = pimqks fsm |
|
gik = pimqks fms |
|
gik = pimqsk fsm |
|
gik = pimqsk fms |
|
произведения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
компонент |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
Группа 1 |
g11 |
g12 |
g13 |
g14 |
g11 |
g12 |
g13 |
g14 |
g11 |
g12 |
g13 |
g14 |
Группа 2 |
g21 |
g22 |
g23 |
g24 |
g11 |
g12 |
g13 |
g14 |
g11 |
g12 |
g13 |
g14 |
Группа 3 |
g31 |
g32 |
g33 |
g34 |
g11 |
g12 |
g13 |
g14 |
g11 |
g12 |
g13 |
g14 |
Группа 4 |
g41 |
g42 |
g43 |
g44 |
g11 |
g12 |
g13 |
g14 |
g11 |
g12 |
g13 |
g14 |
Схема |
gik = pmiqsk fsm |
|
gik = pmiqsk fms |
|
gik = pmiqks fsm |
|
произведения |
|
|
|
|
|
|
|
|
|
|
|
|
компонент |
|
|
|
|
|
|
|
|
|
|
|
|