Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет кораблестроения им. адм. Макарова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Kuznecov_reshebnik

.pdf

Скачиваний:

1096

Добавлен:

15.02.2015

Размер:

4.95 Mб

Скачать

☆

<<< < Предыдущая 8 9 10 11 12 13 14 15 16 17 18 1920 / 3220 21 22 23 24 25 26 27 28 29 30 31 32 > Следующая >>>

Уравнения второго и высшего порядка. Частные случаи уравнений...

z	dz	(1 + p2 ) = 3 pz2 ln	zC	=	3	ln (1 + p2 ) C z = (1 + p2 )3	;


	dp		1		2	1

C1	dp	= dx ;
	+ p2 )3
(1

C1 sin t = x + C2 или

p = tg t

C1 p

1+ p2

,	dp =	dt	; C1 ∫	dt cos3 t	= x + C2
				cos2 t
		cos2 t

= x + C2; C12 p2 = (x + C2 )2 + p2 (x + C2 )2

(x + C2 )2

dy =

(x + C2 )dx

;

C12 − (x + C2 )2 ,

C12 − (x + C2 )2

y = − C12 − (x + C2 )2 − C3 = (y + C3 )2 + (x + C2 )2 = C12 .

317 (4217).

′′

′ ′′′

y′

2 .

( y )

− y y

Решение

y′

′

x = z ,

y′ = zx , y′′ = z + z′x , y′′′

= z′ + z′ + z′′x = 2z′ + z′′x ; (z +

z x)

−

− zx (2z′ + z′′x) = z2

z2 + 2zz′x + z′2 x2 − 2zz′x − zz′′x2 = z2

z′2 = zz′′,

z = p , z′′ = p dp ; p2 = zp dp

p = z dp p = C z ;

= C1z

C x

xeC1x

= C x + C′′

z = C′ xe 1

;

y = C

′

dx + C

= C′

−

2 ∫

∫e

C1x

−

dx + C3 ;

x = u, du = dx,

dx = dv, v =

;

C x

C′

y = C2e

x − C

+ C3

C2 =

191

Решебник задач по теме "Дифференциальные уравнения"

Приближенные решения

318 (4218). При исследовании колебания материальной системы с од-

ной степенью свободы встречается дифференциальное уравнение вида

y′′ =

f1 (x) + f2 ( y) +

f3 ( y′). Решить это уравнение графически, если

f (x) = −x , f

( y) = 0, f

( y′) = −0,1y′

− 0,1y′3 ,

= 0

= y′

x = 0

=1 .

Решение

y′′ = −x − 0,1y′ − 0,1y′3 .

Теоретическое обоснование графического метода интегрирования

дифференциальногоуравненияможнонайтивкниге[9]:

R =

(1)

cos3 ϕ f (x, y, tgϕ

)

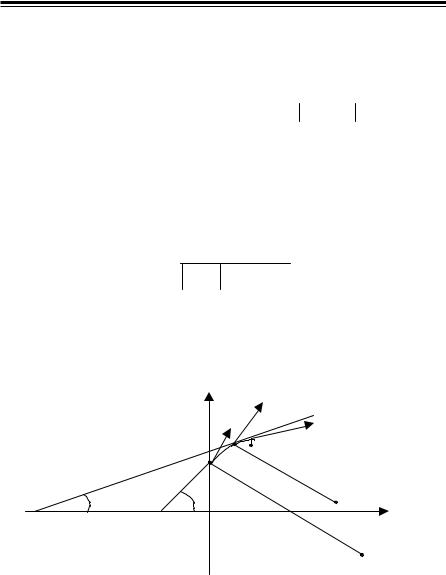
Через точку M

(0; 1) проведем луч M T

(см. рисунок) с угловым

коэффициентом

y′ = tg ϕ 0 = 1

ϕ 0 = 45° .

M1 M2C2

19°

45°

Изуравнения(1) находимвеличину

R0	=	1		= −14,7.
		3 (−0,1
	0,707		− 0,1)

192

Уравнения второго и высшего порядка. Частные случаи уравнений...

Отложим отрезок М0С0 = 14,7 (так как R0 < 0, то отрезок М0С0 нужно направлять в такую сторону, чтобы дуга окружности была обращенавыпуклостьювверх) наперпендикулярекнаправлениюМ0 T0, ииз точки С0 (как из центра) опишем небольшую дугу М0 М1 радиусом R0. Координаты точки M1 (l,2; 2), ϕ 1 = 40°. Тогда

R1	=		1		= −2,169.
		0,7663 (−1,2	− 0,1
				0,84 − 0,1 0,843 )

Приэтомtg ϕ 1 – угловойкоэффициенткасательнойМ1T1, проведенной к окружности в точке М1.

Из (1) нашли, что R1 = –2,169. Проведем отрезок М1С1 = R1 и перпендикулярный к М1T1. Из точки С1 (как из центра) опишем дугу М1М2 радиусом R1. Затем на этой дуге возьмем близкую к М1 точку M2 (l,7; 2,2) ипродолжимпостроение: ϕ 2 = 19°,

R2	=	1			= −0,27.
		(−1,7 − 0,1 2,9 − 0,1 2,93 )
	0,9453
319 (4219). y′′ = yy′ − x2;		y	x = 0 = 1, y′	x = 0 =1. Найтинесколько первых

членов разложения решения в степенной ряд.

Решение

Ищем решение в виде ряда Маклорена:

y = y(0) +

y′(0)

x +

y′′(0)

x2 +

y′′′(0)

+ ...;

y(0) =1,

y′(0) = 1 ,

y′′(0) =

= 1 1 − 0 = 1;

′′′

= y

′2

+ yy

′′

− 2x, y′′′(0)

= 2 ;

(IV )

′ ′′

− yy

′′′

− 2

;

= 2 y y

+ y y

(IV )

′

′′

− yy

′′′

− 2

; y

(IV )

(0)

= 3 + 2

− 2 = 3 и т. д.;

= 3y y

y =1 + x +

2x3

3x4

+ ... .

193

Решебник задач по теме "Дифференциальные уравнения"

320 (4220). Найтишестьпервыхчленовразложенияврядрешениядиф-

ференциального уравнения y′′ = yy′ − 1x , удовлетворяющего начальным

условиям y

x = 1 =1,

y′

x = 1 = 0 .

Решение

Ищем решение в виде ряда Тейлора:

y = y(1)

y′(1)

(x −1) +

y′′(1)

(x −

2 +

y′′′(1)

−1)3 +

y(IV)(1)

(x −1)

(V)

(1)

′′

′2

′′′

y y − y

(x −1)

+ ... ;

y′′(1) = 1 −

1 = −1

; y

+ x2 ,

y′′′(1) =

−1 − 0 +1 = 0 ;

(IV ) =

( y′′′y + y′′y′ − 2 y′y′′) y2 − 2 yy′( y′′y − y′2 )

−

y′′′y3 − 3y2 y′y′′ + 2 yy′3

−

; y(IV )(1) =

−

= −2; y(V ) =

( y(IV)y3 + 3y′′′y2 y′ − 6 yy′2 y′′ − 3y2 y′′2 − 3y2 y′y′′′ + 2 y′

4 + 6 y′2 y′′y) y4

−

4 y3 y′( y′′′y3 − 3y2 y′y′′ + 2 yy′3 )

;

y(V)

(1)

− 2 − 3

+ 6 =1;

(x −1)2

2(x −1)

(x −1)5

y =1 −

−

+ ... .

321 (4221). Найтивформестепенногорядачастноерешениеуравненияу" =

= x sin y', удовлетворяющееначальнымусловиям y

x = 1

= 0 ,

y′

x = 1

(Ограничиться шестью первыми членами.)

Решение

y = y(1) +

y′(1)

(x −1) +

y′′(1)

(x −1)2 +

y′′′(1)

(x −1)3

y(IV )(1)

(x −1)4

194

Уравнения второго и высшего порядка. Частные случаи уравнений...

y(V )(1)

′′

(x −1)

+ ... ;

y (1)

=1 sin 2 =1 ;

y′′′ = sin y′ + x cos y′ y′′ ;

y′′′(1) = sin

+1 cos

1 =1;

y(IV ) = 2 cos y′ y′′ − xsin y′ y′′2 + x cos y′ y′′′;

(IV)

(V )

′

′′2

(1)

2cos

2 1

−1 sin 2 1+1 cos 2 1

= −1 ; y

= −3sin y

+ 2cos y′ y′′′ − xcos y′ y′′3 − 2xsin y′ y′′ y′′′ + cos y′ y′′′ − xsin y′ y′′y′′′ + + x cos y′ y(IV ) = −3sin y′ y′′2 + 3cos y′ y′′′ − x cos y′ y′′3 −

− 3xsin y′ y′′y′′′ + x cos y′ y(IV) ;

y(V )(1) = −3 + 0 − 0 − 3 = −6 ;

y =

(x −1)

(x −1)2

(x −1)3

−

(x −1)

−

6(x −1)5

+ ... .

322 (4222). Найти в форме степенного ряда частное решение y = f (x) уравнения y′′ = xyy′, удовлетворяющее начальным условиям f (0) = 1, f '(0) = 1. Если ограничиться пятью первыми членами разложения, то будет ли это достаточно для вычисления f (–0,5) с точностью до 0,001?

Решение

y = y(0) +

y′(0)

x +

y′′(0)

y′′′(0)

yIV (0)

yV (0)

+ ...

y′′(0) = 0 ,

y′′′ = yy′ + xy′2 + xyy′′ ;

y′′′(0) =1 , y(IV ) = 2 y′2 + yy′′ + 2xy′y′′ +

+ yy

′′

′ ′′

+ xyy

′′′

2 y

′2

+ 2 yy

′′

′ ′′

+ xyy

′′′

; y

(IV )

(0)

= 2 ;

+ xy y

+ 3xy y

y(V ) = 4 y′y′′ + 2 y′y′′ + 2 yy′′′ + 3y′y′′ + 3xy′′2 + 3xy′y′′′ + yy′′′ + xy′y′′′ +

+ xyy(IV )

= 9 y′y′′ + 3yy′′′ + 3xy′′2 + 4xy′y′′′ + xyy(IV ) ;

y(V )(0) = 3 ,

y =1 + x +

2x4

3x5

+ ... .

195

Решебник задач по теме "Дифференциальные уравнения"

	Тогда	f (−0,5)	≈ 1 − 0,5	−	(0,5)	3	+	2(0,5)	4	, аабсолютнаяпогрешность
	Тогда	f (−0,5)	≈ 1 − 0,5	−	3!		+	4!		, аабсолютнаяпогрешность
					3!			4!
∆ <	3(0,5)5	≈ 0,0005 < 0,001. (Можноограничитьсяпервымипятьючле-
∆ <	5!	≈ 0,0005 < 0,001. (Можноограничитьсяпервымипятьючле-
	5!

намиразложения.)

323 (4223). Найти семь первых членов разложения в ряд решения дифференциального уравнения уу" + у' + у = 0, удовлетворяющего началь-

ным условиям

x = 0 =1 ,

y′

x = 0 = 0 . Какого порядка малости будет

при х →

0 разность у – (2 – х – е– х)?

Решение.

yy′′ + y′ + y = 0 ; y(0) =1, y′(0) = 0 ;

′

y′′(0)

y = y(0) + y (0)x +

y′′′(0)

y(IV )(0)

y(V )(0)

y(VI )(0)

′′

y′

+ ... ;

= −

−1,

′′

= −1;

y′′′ =

− y′′y + y′2

′′′

(IV )

= −[

′′′

′′

′

′ ′′

−

y (0)

y (0) = 1; y

(y y

+ y y

− 2 y y

− 2 yy′(y′′y − y′2 )]

y4 = − y′′′y2 + y′′y′y

− − 2 y′y′′y − 2 y′y′′y + 2 y′3

= −

y′′′y2 − 3y′y′′y + 2 y3

y(IV )(0) = −1;

(V)

= [(y

(IV)

′′′

′

′′

y −

y + 2 y yy − 3y

− 3y′2 y′′− 3y′y′′′y + 6 y′2 y′′) y3− 3y2 y′(y′′′y2− 3y′yy′′+ 2 y′3 )]

y6 =

(IV)

′′′ ′

− 3y

′′2

+12 y

′2

′′

− 6 y

′4

= −

− 4 y y y

y y

y(V )(0) = 4 .

196

Уравнения второго и высшего порядка. Частные случаи уравнений...

Аналогично y(VΙ )(0) = −14 . Таким образом,

y =1 −

−

4x5

−

14x6

+ ... .

Разность

y − (2 − x − e−x ) = 1 −

−

4x5

−

14x6

+ ... −

13x

−

− x − 1 − x +

−

− ...

−

+ ...

y − (2 − x − e−x )

−

13x6

lim

= lim

= const

при k = 5. Следова-

x→

тельно, порядок малости равен 5.

324 (4224). Найти 12 первых членов разложения в ряд решения дифференциального уравнения у" + уу' – 2 = 0, удовлетворяющего начальным

условиям

x = 0 = 0 , y′

x = 0 = 0 . Вычислить интеграл ∫1

y dx с точно-

стью до 0,001. Вычислить y′

x = 0,5

с точностью до 0,00001.

Решение

y = y(0) + y′(0)x +

y′′(0)

y′′′(0)

+ ...

; y′′ = 2 − yy′ ,

y′′(0) = 2 ;

y′′′ = − y′

− yy′′ ,

′′′

0 ;

(IV )

′ ′′

− yy

′′′

= −3yy

′′

− yy

′′′

y (0) =

= −2 y y

− y y

y(IV )(0) = 0 ;

y(V ) = −3y′′2 − 3y′y′′′ − y′y′′′ − yy(IV ) = −3y2 − 4 y′y′′′ − yy(IV) ,

y(V )(0) = −12 ; y(VI ) = −6 y′′y′′′ − 4 y′′y′′′ − 4 y′y(IV ) − y′y(IV ) − yy(V ) =

′′ ′′′

−

′

(IV )

− yy

(V)

(VI )

(0) = 0 ;

(VII )

= −10 y′′′

−10 y′′y

(IV )

−

= −10 y y

5 y y

197

Решебник задач по теме "Дифференциальные уравнения"

− 5 y′′y(IV ) − 5 y′y(V ) − y′y(V ) − yy(IV ) = −10y′′′2 −15y′′y(IV) − 6 y′y(V) − yy(IV),

(VII )

(0)

= 0

; y

(VIII )

′′′

(IV )

′′ (V )

′ (VI )

− yy

(VII )

= −35 y y

− 21y y

− 7 y y

y(VIII )(0) = −504

и т. д.;

y = x2 +

−

7x11

+ ...

;

4400

y dx =

−

x12

+ ... 1

−

∫

720

12 44000

3 60

720

−

+ ... = 0,3333

− 0,0166 + 0,0013 − 0,00013

= 0,317 .

12 4400

14243

погрешность

y′ = 2x −

−

x10 + ... ; y′(0,5) =1− 0,03125+ 0,00078 −

1100

−0,000006 = 0,96953 .

14243

погрешность

325 (4225). Электрическая цепь состоит из последовательно соединенныхиндуктивностиL = 0,4 Гниэлектрическойванны. Вванненаходится литрводы, подкисленнойнебольшимколичествомсернойкислоты. Вода разлагается током, при этом меняются концентрации, а следовательно, и концентрация раствора в ванне. Напряжение на клеммах поддерживаетсяпостоянным(20 В). Количествовещества, выделяющеесяприэлектролизе, пропорциональнотоку, временииэлектрохимическомуэквиваленту вещества (закон Фарадея). Электрохимический эквивалент воды равен0,000187 г/Кл. СопротивлениерастворавначалеопытаR0 = 2 Ом, начальныйток10 А. Найтизависимость(вформестепенногоряда) объема воды в сосуде от времени.

Решение		k = 0,000187 г/Кл, R0 = 2 Ом, I0 = 10 A,
L = 0,4 Гн,	Е = 20 В,	k = 0,000187 г/Кл, R0 = 2 Ом, I0 = 10 A,
V0 =1000 см3,	γ = 1 г/ см3.
По закону Кирхгофа э. д. с. в цепи равна сумме: падению напряже-
ния на индуктивности –		L	dI	= L	d 2Q	, где Q – количество электриче-
ния на индуктивности –		L	dt	= L	dt2	, где Q – количество электриче-
			dt		dt2

198

Уравнения второго и высшего порядка. Частные случаи уравнений...

ства в кулонах, и падению напряжения в электролитической ванне –

IR =

R , гдесопротивление R =

, масса m = m − m

; m = V

γ = V ;

= kQ

; m

= m = V

, m

= 0 ;

k =

1000

= 500 (г/Ом).

Итак, дифференциальноеуравнениезадачи

d 2Q

V − kQ

E = L

(1)

dt2

Если V –

количество

воды

в ванне в момент времени t, то

−V

1 dV

d 2Q

1 d 2V

Vγ = V0 γ − ka ; γ =

Q =

= −

dt ,

= −

dt 2

dt2

= −L

d 2V

−

= 0

dt2

V ′′ +

V ′ +

= 0 .

(2)

k L

Обозначим

a =

= 0,005 ,

b =

0,000187 20

k L

500

0,4

= 0,00935 . Из(2) получимдифференциальноеуравнение

V" + 0,005V V' + 0,00935 = 0.

(3)

Решение дифференциального уравнения (3) ищемввидеряда:

V = V +

V0′

t +

V0′′

t2 +

V0′′′t3 +

V0IV

t4 +

V0V

t5 + ...; V

= 1000;

= −k

= −kI

V0′ = −kI0 = −0,00187, V" = –0,005V V' – 0,00935,

V"0 = 0,005 1000 0,000187 – 0,00935 = 0; V"' = –0,005V' 2 – 0,005V V", V"'0 = –0,005 0,001872 = 2,91 6 10–9; V (IV) = –0,005(3V'V" + VV"');

199

Решебник задач по теме "Дифференциальные уравнения"

V0(IV) = 0,005 1000 2,91 6 10–9 = 14,55 6 10–9 и т. д.;

V =1000 − 0,00187t −10−9 (2,91t3 − 3,64t6 + 3,64t5 − 3,04t6 + 2,17t7 − ...).

Рядзнакочередующийся, коэффициенты, начинаясшестого, убывают, стремясь к нулю, что удобно для вычисления.

326 (4226). Электрическая цепь состоит из последовательно соединенных индуктивности L = 0,4 Гн и электрической ванны, первоначальное сопротивление которой 2 Ом. В ванне в литре воды растворено 10 г хлористого водорода. Кислота разлагается током, при этом меняется концентрация раствора (ср. с предыдущей задачей, где количество растворенного вещества не менялось, а менялся объем растворителя). Напряжение на клеммах цепи 20 В, электрохимический эквивалент k хлористого водорода равен 0,000381 г/Кл, начальный ток 10 А. Найти зависимость (в форме степенного ряда) между количеством соляной кислоты в растворе и временем.

Решение

Дифференциальноеуравнениезадачиимеетвид

	d 2Q		dQ		k
L		+		1		= E .
	dt2		dt		M 0 − kQ

Взяввкачествеискомойфункцииколичество у хлористоговодорода, не разложившегося к моменту t, приведем уравнение к виду

yy′′ + ay′ + by = 0 , где a = kL1 = 50 , b = kEL = 0,0191. Интегрируяэтоурав-

нениеприначальныхусловияху0 = М0 = 10; y0′ = −kI0 = −0,00381, полу-

чим ряд y =10 − 0,00381t +10−10 t3 (1,21−1,52t + ...) .

200

<<< < Предыдущая 8 9 10 11 12 13 14 15 16 17 18 1920 / 3220 21 22 23 24 25 26 27 28 29 30 31 32 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.02.2015249.86 Кб7Kursova_robota_pochti_gotovaya.doc
#
15.02.20151.24 Mб16Kursovoy_Sistemy.docx
#
09.12.2018274.43 Кб9kurs_9.doc
#
19.08.2019138.24 Кб1Kurs_lektsiy.doc
#
15.02.2015979.17 Кб19Kuznecov_Praktikum.pdf
#
15.02.20154.95 Mб1096Kuznecov_reshebnik.pdf
#
15.02.20158.28 Mб43Kvasnickij_Pajka_mat.pdf
#
14.02.2015755.2 Кб41Lab1_kl_metod.doc
#
14.02.20152.66 Mб34Lab2_KL_metod.doc
#
14.02.2015547.06 Кб26Laba_1.docx
#
14.02.2015177.15 Кб7Laba_2.doc