Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет кораблестроения им. адм. Макарова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Kuznecov_reshebnik

.pdf

Скачиваний:

1096

Добавлен:

15.02.2015

Размер:

4.95 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 329 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Уравнения первого порядка

136(4036). x dx + y dy + x (x dy − y dx) = 0 .

Решение

x′ +1

+ x

− x x′ = 0,

= u, x′ = y u′ + u; u u′ y + u2 +1 + u y (u −

− y u′ − u) = 0

u u′ y ( y −1) = u2 +1

u du

−

u2 +1

y ( y −1)

y −

− dy

1 ln (u

2 +1) = ln C y −1

u2 +1 = C

y −1; u2

+1 =

C ( y −1)2

(C = C2 ),

x2 + y2

= C ( y −1)2

x2 + y2 = C ( y −1)2 .

137(4037). (x2 + y2 + y) dx = x dy .

Решение

x2 + y 2 + y = x y′,			y	= u, y = u x, y′ = x u′ + u; x2 + u2 x2 + u x = x2 u′ +
x2 + y 2 + y = x y′,			x	= u, y = u x, y′ = x u′ + u; x2 + u2 x2 + u x = x2 u′ +
			x
+ x u	du	= dx;		arctg u = x + C u = tg (x + C); y = x tg (x + C).
+ x u	+ u2	= dx;		arctg u = x + C u = tg (x + C); y = x tg (x + C).
1

В задачах 138 (4038)–147 (4047) решить уравнения Бернулли.

138(4038). y′ + 2 xy = 2 x3 y3.

Решение

Разделиввсечленыуравненияна у3, получим y−3 y′ + 2 x y−2 = 2 x3.

		Замена переменной: z = y−2, z′ = −2 y−3 y′ y−3 y′ = −	1	z′;

	2
−	1	z′ + 2 x z = 2 x3 z′ − 4 x z = −4 x3, z = u v, z′ = u′ v + v′ u;			u′ v +
	2
+ v′ u − 4 x u v = −4 x3, u′ v + u (v′ − 4 x v) = −4 x3; v′ − 4 x v = 0					ln \| v \|=

Решебник задач по теме "Дифференциальные уравнения"

= 2 x2

v = e2x2 ;

e2 x2

= −4 x3

du = −4 e−2 x2 x3 dx

u =

= −4 ∫ e

−2 x2

dx;

= u1, du1 = 2 x dx,

x dx e

−2x2

= dv1, v1 = −

−2 x

;

−2 x2

∫

−2x2

−

2x2

−2 x2

u = −4

−

2 x e

= x

+ C;

= x2 +

+ C ex2 .

139 (4039).

y′ +

+ y2

= 0.

Решение

y′y−2 +

y−1

+1 = 0. Обозначим y−1 = z,

z′ = − y−2 y′. Тогда − z′ +

x +1

+1 = 0, z = u v , z′ = u′ v + v′ u , u′ v + v′ u −

= 1,

u′ v + u

v′ −

=1;

v′ −

= 0

v = x +1;

(x +1) = 1

du =

u =

x +

= C + ln | x +

1|; z = u v = (x +1) (C + ln | x +1|) ; y =

(x +1) (C + ln | x +1|)

140 (4040). yn − 1 (a y′ + y) = x .

Решение

′

n−1

= x , z =

′

n − 1

′

+ z

= x, z = uv, z′ = u′v + v′u ;

ay y

+ y

= ny

y ;

= −dx

−nx / a

u′v + u

v′

+ v

= x ,

= e

;

= x

Уравнения первого порядка

du =

xenx / adx

u =

xenx / adx

;

= u ,

dx = du , enx / adx =

a ∫

nx / a

∫

nx / a

= dv1, v1 =

;

u =

−

−nx

/ a

−nx

/ a

= yn

x −

+ C

; z = uv =

(x −

) + Ce

nyn = Ce−nx / a + nx − a (C = nC ) .

141 (4041).

x dx =

− y

dy.

Решение

xx′ = x2 y−1 − y3, x2 = z , 2 xx′

= z′;

z′ = zy−1 − y3, z = uv, z′ = u′v + v′u;

)= −2 y

′

−1

= −2 y

′

− 2vy

−1

= 0

u v

+ v u − 2uvy

u v + u (v

; v′ − 2vy

= 2

v = y ;

= −2 y

du = −2 y dy

u = − y

+ C ;

x2 = y2 (C − y2 ).

142 (4042). xy′ + y = y2 ln x.

Решение

xy′y−2 + y−1 = ln x, y−1 = z, z′ = − y−2 y′; − x z′ + z = ln x, z = u v,

z′ = u′ v + v′ u; − x u′ v − x v′ u + u v = ln x, − x u′ v − u (x v′ − v)= ln x;

x v′ − v = 0	dv	=	dx	v = x;	− x2	du	= ln x	du = −	ln x	dx u =
	v		x			dx
									x2

Решебник задач по теме "Дифференциальные уравнения"

= −

∫

ln x

dx;

;

ln x

ln x = u1, du1

= dv1, v1 = −

u = −

−

∫

−1

1 = y (ln x +1 + C x).

(ln x +1) + C ; z = ln x

+1 + C x = y

143 (4043). y′ − y tg x + y 2 cos x = 0.

Решение

−2

′

− y

−1

tg x + cos x = 0 ,

−1

= z ,

′

= − y

−2

′

− z′ − z tg x + cos x = 0,

y ;

z = u v, z′ = u′ v + v′ u;

u′ v + u(v′ + v tg x) = cos x ;

v′ + v tg x = 0

= −tg x dx

d(cos x)

v = cos x ;

cos x = cos x

du = dx ;

cos x

u = x + C; y −1 = ( x + C ) cos x ;

y (x + C) = sec x.

144 (4044). y′ +

2 y

2 y .

cos2 x

Решение

y = z

, y′ = 2 z z′,

2 z z

′

2z2

′

;

cos2

cos2 x

= 0

z = u v, z′ = u′ v + v′ u ; u′ v

+ u v′

; v′

cos2 x

u = ∫

x dx

= x tg x − ∫ tg x dx =

= −

v =

;

cos2 x

= x tg x + ln | cos x | +C ;

x = u ,

dx = du ,

= dv ,

= tg x

;

cos

z = tg x +

ln | cos x | + C

= y

ln | cos x | + C

tg x +

Уравнения первого порядка

145 (4045). x y′ − 4 y − x2 y = 0 .

Решение

y = z , y = z2 , y′ = 2 z z′ , 2 x z z′ − 4 z2 − x2 z = 0; 2 x z′ − 4 z − x2 = 0,

z = u v, 2 x u

′

v + 2u (x v

− 2 v) − x

= 0

; x v′ − 2 v = 0, v = 2

v = x

;

2x3

= x2 du =

u =

ln | C x |;

z = x2

ln | C x |= y ;

2 x

y =

ln 2 | x C | .

146 (4046).

y dy −

ay2

dx =

b dx

Решение

y y′ −

a y2

y2 = z , 2 y y′ = z′ ;

2av

2 b

; v′

2av

u′ v + u v′

−

= 0

z′ −

a z

, z = u v ,

2a dx

ln | v |= −

2 a

v = e−2a / x ;

e−2a / x =

u = −

e2a / xd

= −

e2a / x + C ;

2a ∫

z = − b + C e−2a / x ;

y2 = C e−2a / x −

147 (4047). y′

y ϕ

′(x) − y2

, где

ϕ (х) – заданная функция.

(x)

Решение

′

−2

′

−1

′

−1

= z, − y

−2

′

;

y ϕ (x) = yϕ

(x) − y

ϕ (x) =

( x) −1, y

= z

Решебник задач по теме "Дифференциальные уравнения"

− z′ϕ (x) − zϕ ′(x) = −1 , z = u v , u′vϕ (x) + u(v′ϕ (x) + v ϕ ′(x))= 1;

v′ϕ (x) + v ϕ ′(x) = 0

= −

ϕ ′(x) dx

v =

;

=1 u = x + C,

ϕ (x)

z =

x + C

;

y =

ϕ (x)

x + C

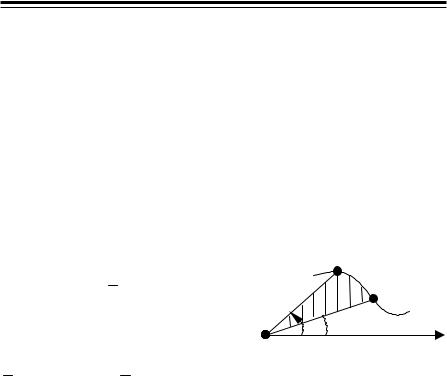
148 (4048). Найтилинию, укоторойотрезок, отсекаемыйнаосиординат касательнойвпроизвольнойточке:

1)пропорционаленквадратуординатыточкикасания;

2)пропорционаленкубуординатыточкикасания.

Решение

1) ON = k y2, y + x tg β = k y2,

y
N	β	M
y
		α
O	x
		x

y − x tg α = k y2, y − x y′ = k y2,

y−1 − x y′y−2 = k, y−1 = z, − y−2 y′ = z′,

z + z′ x = k , z = u v ; u v + x u′ v + x v′ u = k,

u (v + x v′) + x u′ v = k, v + x v′ = 0	dv	=
	v

= − dx		v =	1	; du = k dx u = k x + C ;
x			x

z = k + Cx , 1y = k + Cx

2) y − x y′ = k y3 ,

z + 12 x z′ = k, z = u v ,

−

=1;

= 1

−

= a,

= b .

y−2 − x y′ y−3 = k, y−2 = z , z′ = −2 y−3 y′,

u v + 1 u′ v x + 1 u v′ x = k,

′

u v +

v x

u′ v x = k,

= −2

v =

= k du = 2x dx k;

Уравнения первого порядка

u = k x2 + C , z = k +

= k +

−

=1 ;

= 1

−

= a,

= b .

149 (4049). Найти линии, заданные уравнениями вида ρ = f (ϕ ), для которых площадь секторов, ограниченных линией и полярным радиусом постояннойточки(ρ 0 иϕ 0) итекущейточки(ρ , ϕ ) линии, пропорциональна произведению полярных координат ρ и ϕ этой текущей точки. Коэффициентпропорциональностиравенk.

	Решение
		1	ϕ
	По условию	1	∫ ρ 2 dϕ = k ρ	ϕ .		ρ
		2	ϕ 0			ϕ	ρ	ρ 0 = ρ (ϕ )
			ϕ 0			ϕ	ρ	0
	Возьмем от обеих частей исходно-					ϕ	0	x
гоуравненияпроизводнуюпоϕ :								x
1	ρ 2 = k ρ ′ϕ + k ρ	,	1 = k ρ ′ ρ −2ϕ + k ρ −1		, ρ −1	= z , z′ = −ρ −2ρ ′;
2			2

= −k z′ϕ + k z ,

z = u v,

= −k u′ v ϕ − k u (v′ ϕ − v),

dϕ

v = ϕ ,

= −k

ϕ 2

du = −

dϕ

u =

+ C; z =

+ Cϕ

2 k ϕ 2

2 k ϕ

2 k

dϕ

+ Cϕ .

2 k

При ϕ

= ϕ 0

= ρ 0

+ C ϕ 0

C =

−

;

ρ 0

2 k

ρ 0

2 k

ρ −

(ρ 0 −

2k )ϕ

−

2 k

ρ 0

2 k

ρ 0 ϕ

Решебник задач по теме "Дифференциальные уравнения"

Уравнения в полных дифференциалах

В задачах 150 (4050)–157 (4057) найти общее решение.

150(4050). (2 x3 − x y2 )dx + (2 y3 − x2 y)dy = 0 .

Решение

1-й способ. P = 2 x3 − x y2 ,

Q = 2 y3 − x2 y ;

∂ P

= −2 x y,

∂ y

∂ Q

= −2 x y ;

∂ u

= 2 x3 − x y2

u = ∫ (2x3 − x y2 )dx + ϕ

( y) =

−

∂ x

−

x2 y2

+ ϕ ( y);

∂ u

= −x2 y + ϕ ′( y)

− x2 y + ϕ ′( y) = 2 y3 − x2 y

∂ y

ϕ ′( y) = 2 y3; ϕ ( y) = 2 y3 dy + C

ϕ 4

+ C , u (x, y) =

−

x2 y2

∫

+ C .

По условию du (x, y) = 0

u (x, y) = C2 . Тогда

−

x2 y2

+ C

= C

x4 − x2 y2 + y4 = C .

(1)

2-й способ. u (x, y) = ∫ P (x, y0 ) dx +

∫Q (x, y) dy + C1 .

Пусть

x0 = y0= 0 . Тогда u (x, y) = ∫x

(2 x3 − x 0)dx +

+ y (2 y 3 − x 2 y ) dy + C

; u (x, y) =

−

x2 y2

+ C .

∫

Из u (x, y) = C2 получаем ответ (1).

Уравнения первого порядка

x dy

151 (4051).

−1 dx .

+ y

Решение

P =1

−

, Q =

;

∂ P

= −

2x y

∂ Q

= −

2x y

;

x2 + y2

∂ y

x2 + y2

∂ x

x2 + y2

x0 = y0 = 1 , u ( x, y) = ∫ P (x, y) dx + ∫ Q (x0 , y) dy ; u (x, y) =

1 −

+ C

= x − arctg

+ arctg y

+ C

∫1

+ y

∫1

1 + y

= x − arctg

−1 + arctg

+ arctg y − arctg 1 = C2

x − arctg

= C

arctg y

+ arctg

152(4052). e ydx + ( x e y − 2 y) dy = 0 .

Решение

∂ P

∂ Q

= e

; x0

= y0 = 0 , u (x, y)

∫

P (x, y) dx +

∫

Q (0, y) dy +

∂ y

+ C1 = ∫e ydx − ∫

2 y dy + C1 = x e y

− y2

+ C1 = x e y − y2 + C1 ;

xe y − y2 + C1 = C2 ; x ey − y2 = C .

Решебник задач по теме "Дифференциальные уравнения"

153(4053). y x y − 1dx + x y ln x dy = 0 .

Решение

∂ P	= x y −1 + y x y − 1 ln x;	∂ Q	= x y − 1 + y x y − 1 ln x; x0 = y0 = 1, u (x, y) =
∂ y	= x y −1 + y x y − 1 ln x;	∂ x	= x y − 1 + y x y − 1 ln x; x0 = y0 = 1, u (x, y) =
∂ y		∂ x
x	y		x	y
= ∫ P (x, y) dx + ∫Q (1, y) dy + C1 = ∫ y x y −1				dx + ∫ 0 dy + C1 = x y	x	+
= ∫ P (x, y) dx + ∫Q (1, y) dy + C1 = ∫ y x y −1				dx + ∫ 0 dy + C1 = x y	1	+
1	1		1	1

+ C1 = C2 ; x y = C.

154 (4054).

x dx + y dy = y dx − x dy .

x2 + y2

Решение

−

dx +

dy = 0 ;

x2 + y2

∂ P

2 x y

∂ Q

2 x y

= 2 (x2 + y2 )

− x2 ;

2(x2 + y2 ) x2 + y2

− x2 .

∂ y

x2 + y2

∂ x

Пусть x0 = y0 = 1 ;

u (x, y) = ∫ P (x, 1) dx + ∫ Q (x, y) dy ; u (x, y) =

x		x			1			y
= ∫		x		−	1		dx +∫
= ∫	x	2	2	−	x	2	dx +∫
1	x		+1		x			1
+ x2 + y2 y +				y y + C				=
			1	x 1			1
			1	x 1

1 1

	y		− 1	dy + C
	y		− 1	dy + C
x	2	2	x	1
x		+1	x

x2 +12 − 2 + 1x −1+

+	y	−	1	+ C = C		;	x2 + y2 + y = C.

	x		x	1	2		x

	x2 +12	x	1	x
=	x2 +12	1	+ x	1	+

x2 + y2 − x2 +1 +

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 329 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.02.2015249.86 Кб7Kursova_robota_pochti_gotovaya.doc
#
15.02.20151.24 Mб16Kursovoy_Sistemy.docx
#
09.12.2018274.43 Кб9kurs_9.doc
#
19.08.2019138.24 Кб1Kurs_lektsiy.doc
#
15.02.2015979.17 Кб19Kuznecov_Praktikum.pdf
#
15.02.20154.95 Mб1096Kuznecov_reshebnik.pdf
#
15.02.20158.28 Mб43Kvasnickij_Pajka_mat.pdf
#
14.02.2015755.2 Кб41Lab1_kl_metod.doc
#
14.02.20152.66 Mб34Lab2_KL_metod.doc
#
14.02.2015547.06 Кб26Laba_1.docx
#
14.02.2015177.15 Кб7Laba_2.doc