Kuznecov_reshebnik

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет кораблестроения им. адм. Макарова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

45 (3945). (xy' − y)arctg

.pdf

Скачиваний:

1256

Добавлен:

15.02.2015

Размер:

5 Мб

Скачать

☆

<<< < Предыдущая 1 23 / 323 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Уравнения первого порядка

35 (3935). y′ = xx +− yy.

Решение
	y	= u		′	1	+ u	du
Обозначим			y = ux,	y′ = u + xu′; u x + u =				x =
Обозначим	x		y = ux,	y′ = u + xu′; u x + u =	1	− u	dx	x =

=	1 + u	− u	x du =	1 + u2	dx;	1 − u	du =	dx
	1 − u			1 − u
								x
					1+ u2

= ∫ dxx + ln c ; arctg u − ln 1 + u2 = ln x + ln c ;

36 (3936). x dy − y dx = y dy .

Решение

Из исходного уравнения следует:

∫1 +duu2 − ∫1u+duu2 =

	y	= ln c	x	2	+ y	2	.
arctg		= ln c	x		+ y		.
	x

dy −

dx =

dy ;

= u, y′ = u + u′x; dy (1 − u)= u dx

y′ (1 − u)= u;

(u dx + x du)(1 − u)= u dx ; u dx + x du − u

dx −

(u + u x)(1 − u)= u

′

− ux du = u dx ; x du

(1 − u)= u 2dx

(1 − u)du

; −

− ln

= ln

u 2

+ c1

−

− ln

= c1; ln

= c (c = −c ).

37 (3937).	y′ =	2xy
			.
		x2 − y2

Решение

Разделим правую часть исходного уравнения почленно на х2 и обо-


значим		y	= u ,
		x

xu′ + u	=		2u
			− u2
	1

y′ = xu′ + u . Тогда

1 − u2

du =

;

− u2

Bu + D

A =1 ,

u (1 + u2)

1 + u2

Решебник задач по теме "Дифференциальные уравнения"

B = −2 , D = 0 ;

x2 + y2 = cy .

38 (3938). y' =

Решение

Обозначим

∫

− ∫

2u du

+ ln c = ln

1 + u2

xy + xy .

y	= u ,	y' = u + xu' ; u + xu' =	1	+ u
x			u

=ln x

xdudx = u1 ; u du =

u 2

= ln

+ ln c ;

y2 = 2x2 ln c x

y = ± x 2 ln c x .

x2 + y2 .

39 (3939). xy' − y =

Решение

Разделим обе части исходного равенства на x:

1 +

y' − x

2 –

= u ,

y' = u'x + u . Тогда u' x + u − u =

1 + u

и обозначим

dx x =

= 1 + u2

du 2

= dx ;

∫

du 2

= ∫ dx

+ ln c1

ln u + 1 + u2 =

1 + u

= ln c

;

u + 1 + u2

= c x

y + 1 + y2

= c x

; x

+ y

= c x

− y

x2 + y2 = c2 x4 − 2c x2 y + y2 ; 1 = c2 x2 − 2c y

c2 x2

= 1 + 2с y

x2 = c2 +

2cy

c = c

Уравнения первого порядка

40 (3940). y2 + x2 y' = xyy' .

Решение

Разделим обе части исходного равенства на xy: xy + xy y' = y'. Обо-

значим

= u , y' = u + xu'

. Тогда

u = (u + xu' )

−

u = u −1 +

x (u −1)

u' ;

u −1 du = dx

cxu = eu e y / x = cy .

41 (3941). y' = e y / x + xy .

Решение

Обозначим

= u ,

y′ = u + xu′ ;

u + xu' = eu + u x

= eu ;

−e−u = ln

= −e− y / x .

42 (3942). xy' = y ln

Решение

Обозначим

= u,

y' = u + xu'

u + u'x = u ln u ;

x = u (ln u −1)

; ∫

= ∫

+ ln c

∫

= ln c

; ln

u (ln u −1)

ln e

u ln u

= ln c

= cx u = ee

y = xe

cx + 1

ln e

43 (3943). (3y2 + 3xy + x2 )dx = (x2 + 2xy)dy.

Решебник задач по теме "Дифференциальные уравнения"

Решение

Разделим обе части исходного равенства на xy dx и обозначим xy = u,

y' = u'x + u. Тогда

3u + 3 +

+ 2

+ 3u

+1 = (1 + 2u)×

(u 2 + 2u +

× (u'x + u); (3u2 + 3u +1)dx = x du + 2ux du + u dx + 2u2dx;

+1)dx = x(1 + 2u)du ;

(1 + 2u)du

∫

+ ln c = ∫

d (u2 + 2u +1)

x =

u2 + 2u +1

−

u2 + 2u +1

− ∫

d (u +1)

= ln

+ 2u

u2 + 2u +1

; ln

;

= −

(u +1)2

u +1

u2 + 2u +1 = cxe−

(x + y)2 = cx3e−

;

x + y

u + 1

44 (3944). y' = x

Решение

(u)

ϕ (u)

Пусть

= u,

y' = u'x + u ;

u'x + u = u +

u'x =

ϕ ' (u)

ϕ '(u)u'x = ϕ

(u);

dϕ

(u)

dϕ

x = ϕ

cx = ϕ

ϕ (u)

В задачах 45 (3945)–48 (3948) найти частные решения дифференциальныхуравнений, удовлетворяющиеданнымначальнымусловиям.

Уравнения первого порядка

Решение

(u'x + u − u)arctg u = 1

y' −

arctg

=1 ,

= u , y' = u'x + u ;

∫

z = arctg u, dz

du,

arctg u =1 ;

arctg u du =

+ ln c

;

+ u

;

dv = du, v = u

u arctg u − ∫

du = ln c

;

u arctg u − ln

u2 +1 = ln c x

y arctg

1 + u 2

= x ln c

x2 + y2

;

= 1

= 0

0 = ln c

c =1 ; y arctg

arctg

x2 + y 2

x2 + y2 = e

= x ln

46 (3946). (y2 − 3x

2 )dy + 2xy dx = 0 ;

= 0

=1 .

Решение

Разделимобечастиисходногоравенстванаxy dx:

− 3

+ 2

= 0,

x (u

− 3)= u (1 − u

);

= u,

y' = u'x + u ; u

−

(u'x

+ u)+ 2 = 0

∫

u2 − 3

= ∫

+ ln c ;

u 2 − 3

;

u(1 − u)(1 + u)

1 − u

1 + u

− A + B − C = 1,

B + C = 0,

B = −1, C = 1 ; − 3ln

+ ln

1 − u

+ ln

1 + u

A = −3

1 − u

x2 − y2 = cy3.

= ln c

= cx

c = −1; y2 − x2 = y3 .

При х = 0

y = 1

−1 = c

Решебник задач по теме "Дифференциальные уравнения"

47 (3947). y′ =	y2		− 2xy − x2		;	y	x = 1 = −1 .

	y	2	+ 2xy − x	2

Решение

Разделим дробь на х2 и обозначим xy = u , y′ = u′x + u . Тогда

u′x + u = u2 − 2u −1 u2u′x + u3 + 2uu′x + 2u2 − u′x − u = u2 − 2u −1; u2 + 2u −1

u′x (u2 + 2u −1)= −(u +1)(u 2 +1);

− ∫

u2 + 2u −1

du = ∫

+ ln c ;

(u +1)

(u2 +1)

+ 2u −1

Bu + c

A + B =1,

B + C = 2,

A = −1, B = 2, C = 0 ;

;

(u +1)(u2 +1)

A + C = −1

u +1

− ln (u2 +1) = ln c

y + x

= cx.

x2 + y2

При x = 1

y = −1

y = −x .

C = 0 . Значит,

48 (3948).

0 ; y

5 .

+ 2x

− y

= 0

Решение

Изисходногоуравнения

y 2

− x ±

x2 + y2

−

1 ±

. Пусть

= u ,

y′ = u + xu′ ;

u'x + u = −1 ±

1 + u2

u'x = − (1 + u2 )±

1 + u2 .

Уравнения первого порядка

Возьмем радикал со знаком плюс (+):

1 − 1

1 + u2

+ u 2

∫

dx + ln c.

x =

udu

1 + u

1 −

Обозначим

1 + u 2

= Z

1 + u2 = Z 2 ; u du = Z dZ ;

∫

Z dZ

Z (1 − Z )

= ∫

+ ln c − ln

1 − Z

= ln c

;

= cx

1 + u

x −

+ y

1 −

= cx

+ y

1 = c x −

Используем начальные условия: 1 = c −

c = −

1 ;

−

5 = x −

− x2 + y2 − ( 5 + x)= x2 + y2 ; 5 + 2 5x + x2 = x2 + y2 ;

y2 = 5 + 2 5x – одно частное решение;

y2 = 5 − 2 5x – другое частное решение, соответствующее радикалу со знаком минус (–).

жна быть функция ϕ

, чтобы общим решением данного уравнения

было

y =

Решение

y′ =

′

+ ϕ

′

;

= u

= u x + u

u x + u = u + ϕ

u x = ϕ

Решебник задач по теме "Дифференциальные уравнения"

Тогда

= ∫

Поусловию

y =

Приравниваем правые части равенств (1) и (2):

∫

= −u

или ϕ

= −

(1)

(2)

50 (3950). Найти линию, у которой квадрат длины отрезка, отсекаемого любой касательной от оси ординат, равен произведению координат точки касания.

Решение

По условию

2 = xy . Тогда

= y

+ x tg (180° − α )= y − xy′ ;

(y − xy′)2 = xy

− y

′

= ±

;

= u , y

′

= u + u x; u

− u x − u =

du dx

= ± u − dx x = ± x

u = x ; ± 2 u +

M(x,y)

x = ce± 2 y / x .

+ ln c = ln x

51 (3951). Найтилинию, укоторойначальнаяординаталюбойкасательной равна соответствующей поднормали.

Решение

По условию

. Из ∆ NMK

tg α =

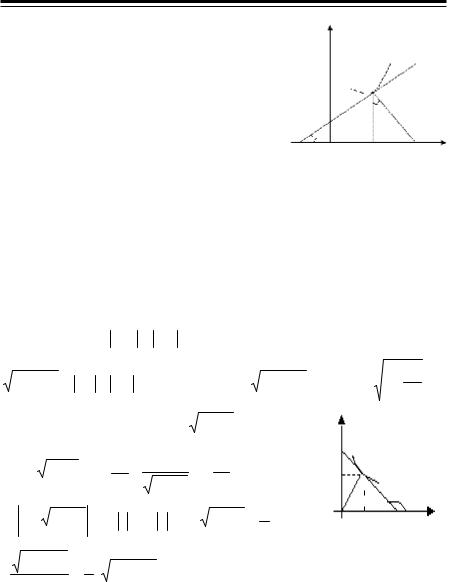
Уравнения первого порядка

= y′;

ctg α =

+ x

= y tg α ctg α = y .

= y′ ;

А.

М(х,у)

Итак,

= u , y′ = u + u′x ;

y + x

C x

N O

u + u′x =

u′x = −

;

u +1

1 + u

(1 + u) du

− ln

= ln

x = y ln

− u2

52 (3952). Найти линию, у которой длина полярного радиуса любой ее точки М равняется расстоянию между точкой пересечения касательной в точке М с осью Оу и началом координат.

Решение

По условию OM = OK . Тогда

x2 + y2 = OL + LK = y + x tg (π − α ) ; x

2 + y2

= y − xy′ ;

1 +

′

1+ u = u − xu

−

= x − y′ ; x = u , y′ = u + xu′ ;

.M(x,y)

−u

1 +u2 = −x dx

;

1 + u2

= − x

ln u + 1 + u2 = ln c − ln x ; u +

1 + u

2 = c

;

+ y2

+ y

= c − y

+ y

= c

− 2cy + y

= x;

; x

= 2cy + c .

53 (3953). Какой поверхностью вращения является зеркало прожектора, если лучи света, исходящие из точечного источника, отразившись, направляются параллельным пучком?

Решебник задач по теме "Дифференциальные уравнения"

Решение

ПустьплоскостьОху– меридианнаяплоскостьповерхностизеркала;

источник света помещаем в точку О(0; 0),

из законов отражения света. Тогда

QO =

OMQ =

OM	=	x	2

MQO – вытекает

+ y	2	.

у M(x,y)

Из ∆

RMQ ctg α =

;

dy =

= x2 + y2 + x ,

= u,

′

;

= u y + u

u′y + u = 1 + u2 + u

= dy

ln u + 1 + u2 = ln c y

;

1 + u

u + 1 + u2 = c y

1 + u

2 = c2 y2 − 2c yu + u2

1 = c

2 y2

− 2c x .

Обозначим

= c

y2 = c2 + 2cx .

Линейные уравнения

В задачах 54 (3954)–64 (3964) найти общие решения уравнений.

54 (3954). y′ + 2y = 4x .

Решение

y = uv, y′ = u′v + uv′; u′v + uv′ + 2uv = 4x; u′v + u (v′ + 2v) = 4x; ν ′ + 2v =

= 0

= −2 v = e−2x; u′e−2 x = 4x

du = 4e2 x x dx ; u = 4∫e2x x dx =

2 x

∫

Z = x,

dZ = dx, e

dx = dq, q =

u = 4

−

= 2xe2x − e2x + c ; y = uv = 2x −1 + ce−2x .

<<< < Предыдущая 1 23 / 323 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.02.20151 Мб21kursovaya_Voznyy_1.doc
#
15.02.201568 Кб50KURSOVAYa2.docx
#
14.02.2015162 Кб12kursovaya5.doc
#
15.02.20151 Мб16Kursovoy_Sistemy.docx
#
15.02.2015979 Кб26Kuznecov_Praktikum.pdf
#
15.02.20155 Мб1256Kuznecov_reshebnik.pdf
#
15.02.20158 Мб55Kvasnickij_Pajka_mat.pdf
#
01.04.2025143 Кб2L_LLL.DOC
#
14.02.2015182 Кб8L_r_Rozdil_II_M.doc
#
14.02.2015266 Кб23Lab__09_EXCEL_Sortirovka_i_filtratsia_dannykh.doc
#
14.02.2015372 Кб43lab_1.doc