Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет кораблестроения им. адм. Макарова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Kuznecov_reshebnik

.pdf

Скачиваний:

1095

Добавлен:

15.02.2015

Размер:

4.95 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 326 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Уравнения первого порядка

B = −3 ; ln y2 = ln (U −1)2

y2 =

(U −1)2 C

+ ln

+ ln C

;

U −

y (2x − y)3 = (x − y) C , где C = 8C .

90 (3990).

xcos y + sin 2 y

Решение

dx = x cos y + sin 2 y ,

x = UV ,

x′y = U ′V + V ′U; U ′V +V ′U −UV cos y =

= sin 2 y

U ′V + U (V ′ −V cos y) = sin 2 y ; V

′ −V cos y = 0

= cos y dy

= sin y

V = esin y ;

dU esin y = 2sin y cos y

dU =

= 2e− sin y sin y cos y dy ; U = 2∫e−sin y sin y cos y dy = 2∫ e−z z dz =

z = U1, dU1 = dz,

= 2(−ze−z + ∫e

−z dz) =

= sin y = z, cos y dy = dz

−z

= dV1

, V1 = −e

−z

= −2e−z (z +1) + C = −2e−sin y (sin y +1) + C; x = UV = − 2(sin y +1) + Cesin y .

91 (3991). (x − 2xy − y2 )dy + y2dx = 0 .

Решение

(y2V ′ +

x − 2xy − y2 + y2 x′ = 0 , x = UV , x′ =U′V +V ′U ; y2U ′V + U

′ +V (1 − 2 y))= y

′

−1)

(2 y −1) dy

;

y V

= V (2 y

V =

Решебник задач по теме "Дифференциальные уравнения"

ln y2 + 1/ y

2 1/ y

2 dU

2 1/ y

dU =

= 2 ln

= e

= y

;

= y

(1+ Ce1/ y ).

∫

= e− 1/ y

U =

e− 1/ yd

−

= e− 1/ y + C;

x = y2

92 (3992). y′ + y cos x = sin x cos x .

Решение

y = UV ,

y′ = U ′V + V ′U ;

U ′V + V ′U + UV cos x = sin x cos x ;

U ′V + U (V ′ + V cos x) = sin x cos x ; V ′ +V cos x = 0

= −cos x dx

V = e−sin x;

dU e−sin x = sin xcos x

dU = esin x sin x cos x dx ;

U = ∫esin x sin xcos x dx = ∫ez z dz =

cos x dx =

sin x = z,

= dz

z = U1,

dz = dU1,

sin x

ez dz = dV ,

= ez = e

( z −1) + C = e

(sin x

− 1) + C ;

y = UV = sin x −1 + Ce− sin x .

93 (3993). (x + 1) y′ − ny = ex (x + 1)n + 1 .

Решение

y = UV ,

y′ = U ′V + V ′U ;

U ′V +V

′U − nUV

= ex (x +1)n ; V ′ −

x +1

= 0

n dx

= nln

x +1

V = (x +1)n ;

(x +1)n = ex (x +

x +1

+1)n

dU = exdx

U = ex + C; y = UV = (ex + C) (1 + x)n .

Уравнения первого порядка

94 (3994). y dx = ( y3 − x) dy .

Решение

yx′ = y3 − x x′ + xy = y2; x = UV , x′ = U ′V + V ′ U ; U ′V +V ′U + UVy =

= y2		V ′ +
= y2	U ′V +U	V ′ +

V	= y2 ; V ′ +	V		dV		dy	ln
			= 0		= −			V	=
			= 0		= −			V	=
		y		V		y
y		y		V		y

= −ln

V =

;

= y3

U =

4xy + C = y4 (C = − 4C ).

95 (3995).

dy 2

+ xy = 0 .

− (x + y)

Решение

x + y ±

+ 2xy + y2 − 4xy

а)

= x

y =

+ C ;

	y3		C
+ C ; x =		+	1

1	4		y

+ y) ± (x − y). 2

б)

= y

= dx ln

yC1

= x

y = Ce

C =

96 (3996). Найти общеерешениедифференциального уравнения

yy′sin x = cos x (sin x − y2 ).

Решение

′

z′

′

sin x = cos x (sin x −

Обозначим y = z, 2 yy

= z , yy′ = 2 . Тогда

− z)

2cos x

z′ +

z = 2cos x

; z = UV ,

z′ = U ′V + V ′U ;

′V +U V ′ +

sin x

Решебник задач по теме "Дифференциальные уравнения"

2 cos x

2cos x

cos x

= 2 cos x; V

′ +

V = 0

= −2

sin x

= −2ln

sin x

V =

;

= 2cos x

U =

sin2 x

= 2∫sin2 x d(sin x) + C ;

U =

sin3 x + C;

y2 =

sin x +

sin

97 (3997). y′ = (x + y)2 .

Решение

Обозначим x + y = z ,

1 + y′ = z′ ,

y′ = z′ −1 . Тогда z′ −

1 = z2

= z2 +1

x + C = arctg z

x + C = arctg (x + y) .

98 (3998). Убедиться в том, что интегральными кривыми уравнения

(1 − x2 ) y′ + xy = ax являются эллипсы и гиперболы с центрами в точке (0; а) иосями, параллельнымикоординатнымосям, причемкаждаякривая имеет одну постоянную ось, длина которой равна 2.

Решение

y′ +

y =

; y = UV

y′ = U ′V + V ′U ; U ′V +U V ′ +

− x2

1− x2

; V ′ +

V = 0

= −

dx ln

1 − x2

− x2

1− x2

а) V = 1− x2 ; б) V = x2 −1 .

Уравнения первого порядка

а) При V =	1 − x2	dU	1 − x2 =	ax	dU = ax (1 − x2 )−3 / 2 dx
		dx		1 − x2
U = a	+ C y = a + C		1− x2	x2 − ( y − a)2		=1	– семейство
1− x2					C2

эллипсов с центром в точке (0; а).

б) При V =	x2 −1	dU	x2 −1 = − ax	dU = −ax (x2 −
		dx	x2 −1
−1)−3 / 2 dx U =	a	+ C	y = a + C x2 −1	x2 − ( y − a)2	=1	–
	x2 −1			C 2

семейство гипербол с центром в точке (0; а).

В задачах 99 (3999)–102 (4002) найти частные решения уравнений, удовлетворяющие начальным условиям.

99 (3999).

y − xy′

= 2 ;

x = 1

= 1.

x + yy′

Решение

− y′

U −U ′ x −U

= 2 ; U′ x (1+ 2U ) =

= 2

;

=U , y′ = U + U ′x ;

1+ U 2 + UU ′ x

y′

= −2 (1+U 2 )

(1+ 2U ) dU

= − 2dx

arctg U = − ln (1 +U 2 )− ln x2 + C ;

1+U 2

arctg

+ ln (x2 + y2 )= C .

+ ln (x2

+ y2 )=

При x = 1 и y = 1

C =

+ ln 2 ;

arctg

+ ln 2 .

100 (4000).

y′ −

= 1 + x ; y

x = 0 = 1 .

− x

Решебник задач по теме "Дифференциальные уравнения"

Решение

= 0

y = UV , y′ = U ′V +V

′U ; U ′V + U V ′

−

= 1 + x; V ′ −

1 − x2

− x2

ln V =

1 1 + x

1 + x

dU 1 + x

1 − x2

2 ln 1− x

1 − x

;

dx 1− x

=1+ x

U = ∫

1− x2 dx + C ;

x = sin z,

dx = cos z dz

;

U = ∫cos2 z dz + C =

∫

(1+ cos 2z) dz =

z +

sin 2z + C

+ C

;

arcsin x + x 1 − x

y =

1 + x

1 − x

+ C

1 + x

arcsin x + x

1 − x

При x = 0

y = 1

C = 2 ;

1 + x

+ 2

arcsin x + x 1 − x

1 − x

101 (4001). (1 + ex ) yy′ = e y ; y

x = 0 = 0 .

Решение

e− y y dy =

ye− ydy =

+ C

;

∫

∫1 + ex

1 + ex

y = U1,

dy = dU1,

1 + ex = z, x = ln (z −

1),

; −ye− y

∫e− y dy =

− y

dy = dV1,

V1 = −e

dx =

z −1

+ C

;

−ye− y − e− y =

− dz + C

; −e− y (1+ y) =

∫ z(z −1)

∫ (z −

1) ∫ z

= ln

z −1

+ C

; e− y (1 + y) = ln

+ C (C = −C ); e− y (1 + y) =

z −1

= ln

ex +1

+ C .

Уравнения первого порядка

При x = 0

и y = 0

C = 1 − ln 2 ; e− y (1 + y) = ln

ex +1

− x +1 .

102 (4002). y′ = 3x2 y + x5 + x2 ;

x = 0 = 1 .

Решение

y = UV , y′ = U ′V + V ′U ; U ′V + U (V ′ − 3x2V )= x5 + x2 ; V ′ − 3x2V =

= 0

= 3x

= x

V = e

;

= x

5 + x2

U =

= ∫e−x

∫e−x

2 dx + ∫ e−x

(x5 + x2 ) dx + C =

dx + C; ∫ x2e−x

= −

3 e−x

Второй интеграл берем по частям: U1 = x3 , dU1 = 3x2 dx ;

∫

dV = e−x3 x2 dx ;

= − 1 e−x3 . Тогда

e−x3 x5dx = −

x3e−x3

+ ∫ x

−x3

dx = −

= −

−x3

+ C , y = UV = −

+ 2) + Ce

Итак,

U = −

+ 2)

При x = 0

и y = 0

1 = −

+ C

C =

;

y =

−

+ 2) .

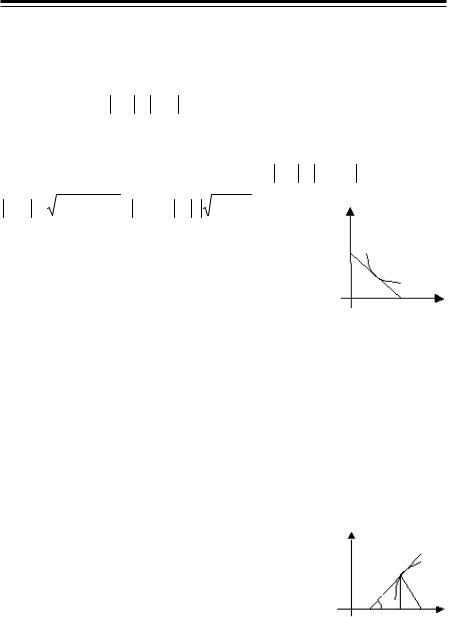
103 (4003). Доказать, что только прямые y = kx и гиперболы xy = m обладают следующим свойством: длина полярного радиуса любой их точки равна длине касательной, проведенной в этой точке.

Решение

По условию OM = MN ; OM = x2 + y2 .

Уравнение касательной к кривой y = f (x) в точке M (x; y) имеет вид

Y − y = y′( X − x) .

Решебник задач по теме "Дифференциальные уравнения"

+ y2

При Y = 0 X = −

+ x , т. е.

−

+ x, 0

;

MN =

;

y′

у
	М(х,у)
	y = f (х)
O	N x

x2 + y2 =

+ y2

xy′ = ± y .

y′2

а) xy′ = y

y = kx – прямые;

б) xy′ = − y

= −

y =

– гиперболы.

104 (4004). Найтилинию, укоторойдлинанормалипропорциональнаквадратуординаты. Коэффициентпропорциональностиравенk.

Решение

Уравнение нормали имеет вид

Y − y = −

(X − x) .

y′

При Y = 0

X = yy′ + x , MN =

y2 y′2 + y2 = y

y′2 + 1 .

По условию y

y′2 +1 = ky2

y′

k 2 y2 −1 ; ∫

−1

= ∫dx + C1

ln ky + k 2 y2 −1

= x + C1 ;

± k

М(х,у)

ky + k 2 y2 −1 = ekx + C (C = C1k);

k 2 y2 −1 =

= ekx + C − ky ;

k 2 y2 −1 = e2(kx + C) − 2kyekx + C +

O N

+ k 2 y2

y =

(ekx + C + e− (kx + C ) ).

Уравнения первого порядка

105 (4005). Найти линию, у которой любая касательная пересекается

сосью ординат в точке, одинаково удаленной от точки касания и от начала координат.

Решение

По условию NO = NM . Уравнение касательной имеет вид

Y − y = y′ ( X − x) .

При X = 0 Y = y − xy′ N (0; y − xy′) , NO = y − xy′ ,

NM = x2 + x2 y′2 , y − xy′ = x 1 + y′2 ,

− 2xyy′ + x

y′

(1 + y′

)

y′ =1

= x

− 2

, y′ = U ′ x + U , U 2 − 2 U 2 − 2 Ux U ′ = 1;

2 U U ′ x = − (1 +U

2 )

2 U dU

= −

ln (1+U 2 ) = ln

1 +U 2

x2 + y2

= Cx .

М(х,у)

1+U 2 =

106 (4006). Найти уравнение линии, пересекающей ось абсцисс в точке x = 1 и обладающей таким свойством: длина поднормали в каждой точке линии равна среднему арифметическому координат этой точки.

Решение

x + y

= y tg α = yy′ , 2 y y′ = x + y ,

М(х,у) .

y′

= U , y′ = U ′ x + U , 2U U′ x +

=1 +

= 1 + U

2 U dU

+ 2U

А Р x

1 + U − 2U 2 = x ,

Решебник задач по теме "Дифференциальные уравнения"

			(−							1	+	1
			(−	4U +1) −							+						dx		1
2∫										4		4	dU =∫										+ U − 2U		2
										4		4													2
																	x ; −			ln		1					+
				1 + U − 2U 2															2	ln		1					+
				1 + U − 2U 2															2							1
							3				1
							3				1
		1 4							+U −																	2 +U		= 6 ln		C x	;
							4		+U −		4								+ U − 2U 2					+ ln
+					ln		4				4	= ln		Cx		,	− 3 ln	1	+ U − 2U 2					+ ln
		2 3 4						3	−U +		1															1 −U				1
		2 3 4						3			1															1 −U
				1			4				4
				1		+U																	(x + 2 y)x6
				2		+U						= Cx6 (C = C 6 )											(x + 2 y)x6						= Cx6 .
	(1 −U ) (1 +U − 2U 2 )3
																					2 (x − y) (x2 + xy − 2 y2 )3
																	1				2 (x − y) (x2 + xy − 2 y2 )3
			При x = 1 и y = 0									C =			1		; (x + 2 y) = ( y − x) ( y − x)3 (x + 2 y)3
			При x = 1 и y = 0									C =					; (x + 2 y) = ( y − x) ( y − x)3 (x + 2 y)3
													2

( y − x)2 (x + 2 y) = 1.

107 (4007). Найти линию, у которой площадь трапеции, образованной осями координат, ординатой произвольной точки и касательной в этой точке, равна половине квадрата абсциссы.

2 y

Решение

По условию SOPMN =

. Тогда

( y +

)x =

y +

= x;

= x ;

= x tg β

= x tg(π − α ) = −x tg α

= −xy′ ; 2 y − xy′ = x ,

y = UV , y′ = U ′V + V ′U ; 2 UV − x U ′V −

− x U V ′ = x , U (2V − x V ′) − x U ′V = x ,

U (2V − x V

′) − x U ′V = x ; − x

β М(х,у)

dU = −

U =

+ C; y = x + Cx2 – семей-

ство парабол.

<<< < Предыдущая 1 2 3 4 56 / 326 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.02.2015249.86 Кб7Kursova_robota_pochti_gotovaya.doc
#
15.02.20151.24 Mб16Kursovoy_Sistemy.docx
#
09.12.2018274.43 Кб9kurs_9.doc
#
19.08.2019138.24 Кб1Kurs_lektsiy.doc
#
15.02.2015979.17 Кб19Kuznecov_Praktikum.pdf
#
15.02.20154.95 Mб1095Kuznecov_reshebnik.pdf
#
15.02.20158.28 Mб43Kvasnickij_Pajka_mat.pdf
#
14.02.2015755.2 Кб41Lab1_kl_metod.doc
#
14.02.20152.66 Mб34Lab2_KL_metod.doc
#
14.02.2015547.06 Кб26Laba_1.docx
#
14.02.2015177.15 Кб7Laba_2.doc