
Kuznecov_reshebnik
.pdf
Уравнения первого порядка (продолжение)
xp2 − 2 yp + 4x = 0 p = |
± |
y2 − 4x2 |
|
|
2 = C x2; |
|
|
|||||||
|
|
; y + y2 − 4x |
|
|
||||||||||
|
|
|
|
|
|
x |
|
|
|
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 − 4x2 |
= C x2 − y |
C |
2 x2 − 2C y + 4 = 0; |
C1 |
= C . Тогда |
|
|
||||||
|
|
|
||||||||||||
|
|
1 |
|
1 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = Cx2 + |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдем из (2) такие р = р |
, при которых |
p |
− |
4 |
= 0 |
p(1) |
= 2 , |
||||||
|
|
|
|
|
|
0 |
|
|
0 |
|
p0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
p0(2) = −2 . |
|
|
|
|
|
|
|
|
|
|
|
||
|
Подставляя эти значения в уравнение |
2 yp = xp2 + 4x , |
получим |
|||||||||||
y = ± 2x или y2 − 4x2 = 0 . Это решение особое, так как не получается из общего ни при каком С.
225(4125). y = yy′2 + 2xy′ – уравнение Лагранжа.
Решение
Положим y′ = p . Тогда
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(1 − p2 )= 2xp . |
|
|
|
|
|
|
|
|
(1) |
||||||||
|
Дифференцируя(1), получим y′(1 − p2 )− 2 pp′y = 2 p + 2xp′ |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− p(1 + p |
2 |
′ |
|
|
|
|
|
|
|
|
|
|
(2) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)= 2 p ( py + x) . |
|
|
|
|
||||||||||||||||
|
Из (1) y = |
|
2xp |
|
. Подставим (1) в (2): |
dx |
|
= |
|
|
|
|
dp |
; |
||||||||||||||||||||||||||||||
|
1 − p2 |
|
2x |
|
( p −1)( p +1) p |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
1 |
|
|
|
|
|
= |
|
|
A |
|
|
|
+ |
|
|
B |
|
+ |
R |
|
|
|
A = 1 , B = |
1 |
, R = −1 . Тогда |
||||||||||||||||||
( p −1)( p +1) p |
p −1 |
p +1 |
|
|
|
2 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
p |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
1 |
ln |
|
x |
|
= |
1 |
ln |
|
p −1 |
|
+ |
1 |
ln |
|
p +1 |
|
− ln |
|
p |
|
+ C |
x = C |
|
p2 |
−1 |
. |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 p |
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
131

Решебник задач по теме "Дифференциальные уравнения"
|
|
x = C1 |
p |
2 |
−1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
p |
2 |
|
2C |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Из системы |
|
|
|
|
|
|
|
|
|
y = − |
|
|
1 |
, 2C |
|
= C, p = y′ . Тогда |
|||||
|
y = |
2xp |
|
|
|
|
|
|
p |
|
|
|
1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 − p |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
y′ = − |
C |
. |
|
|
|
|
|
(3) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
Подставим (3) в исходное уравнение: |
y = y |
C 2 |
− 2x |
C |
|
||||||||||||||||
|
y2 |
y |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2Cx = C2 − y2 – общее решение.
Уравнение (2) обращается в тождество при р = 0. Подставим это значение в (1): y = 0. Но y = 0 не является особым решением, так как получается из общего при С = 0. Значит, особого решения нет.
226(4126). y = x(1 + y′) + y′2 .
Решение
Положим y′ = p . Тогда
|
|
|
|
|
|
y = x(1 + p) + p2. |
|
|
|
(1) |
|||
Дифференцируем (1) пох: y′ =1 + p + x dp + 2 p dp или |
−1 = |
dp |
(x + |
||||||||||
dx |
|||||||||||||
|
|
|
|
|
|
|
|
dx |
dx |
|
|
||
+ 2 p) |
|
dx |
+ x = −2 p; x = uv, x′ = u′v + v′u , u′v + u(v′ + v) = −2 p ; v′ + v = |
||||||||||
|
dp |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
dv |
|
|
du |
|
|
|
|
|
||||
= 0 |
|
= −dp |
v = e− p ; |
|
e− p = −2 p ; u = −2∫ pe pdp = −2 pe p + |
|
|||||||
v |
dp |
|
|||||||||||
+ 2e p + C ; |
[p = u , dp = du , e pdp = dv , v = e p ]; |
x = uv = −2( p −1) + |
|||||||||||
|
|
|
|
1 |
1 |
1 |
1 |
|
|
|
|
||
+ Ce− p .
Итак, общее решение y = x(1 + p) + p2 ; x = −2( p −1) + Ce− p .
132

Уравнения первого порядка (продолжение)
Особое решение ищем из системы
|
y = x(1 |
+ C) + C2 , |
|
x = −2C, y = −2C − C |
2 |
= const; ноэтонеудовлетво- |
|
0 = x + |
2C |
|
|||
|
|
|
|
|
ряетисходноедифференциальноеуравнение, таккактогдаимеем {y = x.
const
Особого решения нет.
227(4127). y′ = ln(xy′ − y) .
Решение
Положим y′ = p . Из условия задачи имеем
|
|
|
|
xy′ − y = e y′ или |
xp − y = e p. |
(1) |
||||
Дифференцируем(1) пох: |
|
|
|
|
||||||
p + x |
dp |
− p = e p |
dp |
|
dp |
(x − e p ) = 0 |
|
dp |
= 0 |
p = C. |
dx |
dx |
|
|
dx |
||||||
|
|
|
dx |
|
|
|
||||
Общее решение получаем из (1), подставляя в него р = С: y = Cx − eC .
При p = ln x получаем особое решение: y = x(ln x −1) . Оно не может быть получено из общего ни при каком С.
228(4128). y = y′(x + 1) + y′2 .
Решение
Положим y′ = p . Тогда
|
|
|
y = p(x +1) + p2 . |
|
(1) |
|||
Дифференцируем(1) пох: |
|
|
|
|
|
|||
y′ = (x +1) dp |
+ p + 2 p dp |
|
dp |
(x +1+ 2 p) = 0 |
dp |
= 0 p = C . |
||
dx |
dx |
|
dx |
|
dx |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
||||
Общее решение получаем из (1): y = Cx + C + C2 .
133

Решебник задач по теме "Дифференциальные уравнения"
Далее имеем x +1 + 2 p = 0 |
p = − |
1 |
(x +1). Подставляем p в (1) |
|||||||||
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
иполучаемособоерешение: y = − |
1 |
(x +1) |
2 + |
1 |
(x +1)2 |
и |
y = − |
1 |
(x +1)2. |
|||
2 |
4 |
4 |
||||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
229(4129). y = y′x + a 3 1 − y′3 .
1 − y′3 .
Решение
Положим y′ = p . Тогда y = px + a 3 1 − p3 . Дифференцируемпослед-
нее выражение по х: |
y′ = |
dp |
x + p |
+ |
1 |
a |
(1 |
− p3 )−2 / 3 |
|
(− 3 p2 ) |
dp |
|
||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
||||
|
dp |
|
|
|
|
p2a |
|
|
|
|
|
dp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x − |
|
|
|
|
0 |
|
= 0 |
|
|
p = C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
(1 |
|
|
|
|
= |
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
dx |
|
|
|
3 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
3 |
− p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Общеерешениедифференциальногоуравнения: y = Cx + a3 1 − C 3 . |
|||||||||||||||||||||||||||||||||||||
|
|
|
Далеевыполняемпреобразования: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
p2a |
|
|
|
|
|
|
p6a3 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
x3 (1 − p3 )= |
||||||||||||||
|
x = 3 (1 − p3 )2 |
; x3 = |
|
; x3 (1 − p3 ) |
= p6a3 ; |
|
|
|||||||||||||||||||||||||||||||||
|
(1− p3 )2 |
|
|
|||||||||||||||||||||||||||||||||||||
= p3 a3 |
p3 = |
|
x3 |
|
|
|
|
|
p3a |
|
+ a 3 |
(1− p3 )= |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
; y = |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
a3 + x3 |
|
|
|
3 (1− p3 )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
= |
|
a |
|
|
[ p3 + (1− p3 )]= |
|
|
a |
|
|
|
|
= |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
= |
|
|||||||||||
3 |
(1− p3 )2 |
|
|
|
|
|
|
|
3 |
(1− p3 )2 |
|
|
|
|
|
|
|
x |
3 |
|
|
|
2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
1− |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
+ |
|
x |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
a |
3 |
+ |
x |
3 |
2 |
|
y |
3 |
|
|
|
3 |
+ |
x |
3 |
2 |
|
y |
3 |
+ |
x |
3 |
= |
|
a |
3 |
– особое |
||||||||||
= 3 |
|
|
|
|
|
= a |
|
|
|
|
; |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
решение.
134
Уравнения первого порядка (продолжение)
230 (4130). x = |
|
|
|
|
|
|
|
1 |
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
y |
|
|
|
|
|
|
|
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Положим yx′ = |
|
|
|
1 |
|
|
; |
|
x′y = p. Тогда x = y ( |
p − p); |
xy′ = p − p + |
||||||||||||||||||||||||||||||
|
|
|
|
|
xy′ |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
+ y |
|
1 |
|
|
|
dp |
|
|
|
|
|
|
2 p − |
p = y |
1 − |
2 |
|
p |
|
dp |
− p = |
y |
|
dp |
|
|||||||||||||||||||
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 p |
|
|
dy |
|
|
|
2 p dy |
|
|||||||
|
|
|
2 p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
dy |
= − |
|
|
dp |
|
ln |
|
y |
|
= − |
|
1 |
ln |
|
p |
|
+ ln C; |
y = |
|
C |
|
p = |
C |
p = C2 . |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
y |
|
|
|
− 2 p |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
y |
|
|
y2 |
|||||
|
|
|
|
|
C |
|
|
|
C 2 |
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Тогда |
|
x = |
y |
|
− |
|
|
|
|
|
|
|
|
x = C |
1 − |
|
|
|
|
|
(C |
− x) y = C2 |
– общее |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
решение.
x = y ( |
C − C), |
|||
|
|
|
1 |
|
|
0 |
|||
|
= y |
|
−1 |
|
|
|
2 C |
|
|
|
|
|
|
|
C = |
1 |
|
1 |
|
1 |
|
|
y = 4x – особое решение. |
||
4 |
; x = y |
|
− |
|
|
|||||
2 |
4 |
|||||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
В задачах 231 (4131)–233 (4133) найти особые решения уравнений, применяя тот же прием, какой используется в случае уравнений Лагранжа и Клеро.
231(4131). y′2 − yy′ + ex = 0 .
Решение
|
C |
2 |
= yC + e |
x |
= 0, |
C = |
y |
; |
y |
2 |
− |
y |
2 |
+ ex = 0 ; y2 − 4ex = 0 |
– особое |
||
|
|
|
|
|
|||||||||||||
|
2C − y = 0 |
|
|
|
2 |
|
4 |
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||
решение.
135

Решебник задач по теме "Дифференциальные уравнения"
232 (4132). x2 y'2 −2(xy − 2) y′ +
Решение
|
x |
2 |
C |
2 |
− 2(xy − 2) C + y |
2 |
= 0, |
|
|
|
|
|
|
||||
|
2Cx |
2 |
− 2(xy − 2) = 0 |
|
|
|||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
y2 = 0 .
C = |
xy − 2 |
; |
x2 (xy − 2)2 |
− |
2(xy − 2)2 |
+ |
|
x4 |
x2 |
||||||
x2 |
|||||||
|
|
|
|
+ y2 = 0 (xy − 2)2 = x2 y2 xy − 2 = ± xy ; xy =1 – особое решение.
233(4133). y′( y′ − 2x) = 2( y + x2 ) .
Решение
|
C(C − 2x) = 2( y + x2 ), |
|
C = x ; |
x |
2 |
− 2x |
2 |
= 2 y − 2x |
2 |
|
x |
2 |
− 2 y = 0 |
– |
|
|
2C − 2x = 0 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
особое решение.
234 (4134). Доказать теорему: если линейное дифференциальное уравнение является уравнением Клеро, то семейство его интегральных кривых представляет собой пучок прямых.
Решение
Уравнение Клеро имеет вид
|
|
|
y = xy′ + Ψ ( y′) . |
|
|
(1) |
Положим y' = p. Тогда (1) примет вид |
|
|
|
|||
|
|
|
y = xp + Ψ ( p) . |
|
|
(1') |
Продифференцируем(1' ) пох: |
|
|
|
|||
y′ = x dp |
+ p + Ψ ( p) dp |
dp |
(x + Ψ ( p)) = 0 |
dp |
= 0 и |
(x + Ψ ( p)) = 0 . |
dx |
dx |
dx |
|
dx |
|
|
Интегрируя первое из двух последних равенств, получим p = C (C = const). Подставляя это значение p в уравнение (1' ), будем иметь
его общий интеграл y = xC + Ψ (C) , который с точки зрения геометрии
есть семейство прямых линий.
136

Уравнения первого порядка (продолжение)
235 (4135). Площадь треугольника, образованного касательной к искомойлиниииосямикоординат, естьвеличинапостоянная. Найтилинию.
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
y |
|
|
|
|
|
||
Уравнение прямой в отрезках имеет вид |
|
+ |
=1 . Если a2 |
– пло- |
|||||||||||||||||||
|
m |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
||||
щадь∆ |
AOB, то mn = ±2a |
2 |
, т. е. |
n = ± |
|
2a2 |
ииме- |
|
|
y |
|
|
|
||||||||||
|
m |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
ем семейство прямых: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|||||
|
|
|
|
x |
|
my |
|
|
|
|
|
|
|
|
|
M (x, y) |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
||||||
|
|
|
|
|
± |
|
= 1. |
|
|
|
(1) |
|
|
|
|
|
|
|
|||||
|
|
|
|
m |
2a2 |
|
|
|
|
|
|
|
|
|
x |
||||||||
Продифференцируем(1) пох: |
|
|
|
|
|
|
|
|
O m B |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
± my′ |
|
|
|
2a2 |
|
2a2 |
|
|
|
|
|
|
|
|||||||||
= 0 m2 |
= m |
m = ± |
|
|
y = xy′ ± m 2a2 y′. |
||||||||||||||||||
m |
2a2 |
|
|
|
|
y′ |
|
|
|
m y′ |
|
|
|
|
|
|
|
|
|
|
|||
Общеерешениедифференциальногоуравнения: y = xC1 ± |
|
|
|
||||||||||||||||||||
± m2a2C |
y = ± C2 |
x + aC (C2 = |
2C ). |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1 |
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Но нас интересует особое решение, которое даст искомую линию – |
|||||||||||||||||||||||
огибающую семейство прямых. Составляем систему уравнений: |
|
|
|
||||||||||||||||||||
|
C 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = ± |
2 x + aC, 2xy = ± a2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = ± Cx + a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
236 (4136). Найтилинию, касательныеккоторойотсекаютнаосяхкоординат отрезки, сумма которых равна 2а.
Решение
Уравнение прямой в отрезках имеет вид
x |
+ |
y |
= 1. |
(1) |
|
m |
n |
||||
|
|
|
137

Решебник задач по теме "Дифференциальные уравнения"
По условию m + n = 2a n = 2a − m . Подставляем (2) в (1):
|
x |
+ |
|
y |
=1. |
|
|
|
|
(2) |
||||
|
|
|
2a − m |
|
|
|
|
|||||||
|
m |
|
|
|
|
|
|
|
|
|||||
Дифференцируем (2) по х: |
|
1 |
+ |
y′ |
|
= |
0 |
m = |
|
|
2a |
. Тогда урав- |
||
|
2a − m |
1 |
− y′ |
|||||||||||
|
|
m |
|
|
|
|
|
|||||||
нение прямой имеет вид |
x (1− y′) |
+ |
|
|
|
y |
|
=1 или |
||||
|
|
2a |
2a − |
2a |
|
|||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
1 − y′ |
|
|
|||
− |
y (1− y′) |
′ |
|
′ |
|
|
|
′ |
|
|
|
|
2ay′ |
, или (1 − y ) (xy |
|
− y) = 2ay |
|
. |
|
|
|
||||
Общеерешениедифференциальногоуравнения: (1
x (1 − y′) − 2a
− C)(xC −
|
xC − xC |
2 |
− y + y C = 2a C, |
|
x + y − 2a |
|
− y) = 2aC ; |
|
C = |
; |
|||
|
|
2x |
||||
|
x − 2xC + y = 2a |
|
|
|||
|
|
x + y − 2a x + y − 2a |
|
|
x + y − 2a |
|
|
2 |
|
|
– |
||
1 |
− |
|
|
|
− y |
= a |
|
(x + y − 2a) |
|
= 8ax |
|||
2x |
2 |
x |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||
особоерешениедифференциальногоуравнения.
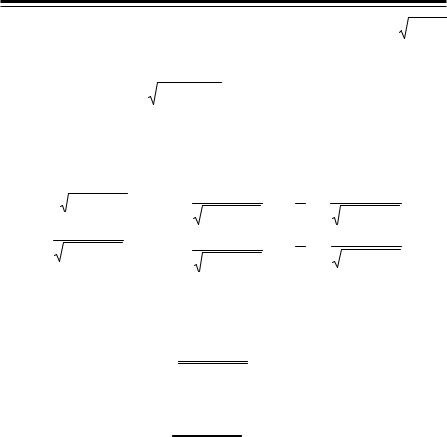
237 (4137). Найти линию, для которой произведение расстояний любой касательной до двух данных точек постоянно.
Решение
y  K
K
Системукоординатрасположимпоотношениюкфиксированным точкам, какпоказанонарисунке. Уравнениекасательнойвточ-
ке M (x; y): Y − y = y′( X − x) или y′X − Y −
d2 |
d1 |
M(x, y) |
− (xy′ − y) = 0 , где X и Y – текущие коорди- |
|
L |
наты точек касательной; F |
и F – фиксиро- |
||
|
|
1 |
2 |
|
F2 (– c, 0) O |
F1 (– c, 0) x |
ванные точки. |
|
|
Расстояния d1 и d2 до прямой KL най- |
||||
|
|
|
дем по известным формулам: |
|
d = ± cy′ − (xy′ − y) |
; d |
2 |
= ± − cy′ − (xy′ − y) . |
1 |
|
y′2 +1 |
|
y′2 +1 |
|
|
138
Уравнения первого порядка (продолжение)
|
|
|
Поусловиюd d = b2 |
(const), поэтому(xy′ − y)2 − c2 y′2 = ± b2 y′2 +1 |
||
1 |
2 |
|
|
|||
или (xy′ − y)2 = (c2 ± b2 ) y′2 ± b2 , |
обозначив c2 ± b2 = a2 (полагаем |
|||||
|
c |
|
< b), имеем y = xy′ ± |
a2 y′2 ± b2 |
– уравнение Клеро. |
|
|
|
|||||
|
|
|
Его общее решение |
представляет собой семейство прямых. Най- |
||
дем особое решение. Для этого продифференцируем общее решение по С и составим систему уравнений:
|
y = cx ± a2c2 ± b2 , |
|
|
|
|
|
|
a2c |
, |
|
x |
= m |
|
|
ac |
|
; |
|||
|
x = m |
a2c2 ± b2 |
|
a |
|
|
|
|
|
|||||||||||
|
|
a2c |
|
|
|
|
|
|
|
|
a2c2 ± b2 |
|||||||||
|
0 = x ± |
|
|
|
|
|
b2 |
|
y = ± |
|
|
b |
|
|
||||||
|
a2c2 ± b2 |
|
|
y |
= ± |
|
|
|
|
2 |
|
. |
||||||||
|
|
|
|
a2c2 ± b2 |
|
|
b |
|
a |
c |
2 |
± b |
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Возьмем знак плюс (+) перед b2, возведем обе части каждого урав- |
|||||||||||||||||||
нения в квадрат и сложим: |
|
x2 |
+ |
y2 |
= 1. Затем возьмем знак минус (–) |
|||||||||||||||
|
a2 |
b2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
перед b2, возведем обе части каждого уравнения в квадрат и вычтем из
первого уравнения второе: |
x2 |
− |
y2 |
= 1 |
. Итак, искомые кривые – эллип- |
|
a2 |
b2 |
|||||
|
|
|
|
сы и гиперболы.
238 (4138). Найти линию, для которой площадь прямоугольника, имеющего сторонами касательную и нормаль в любой точке, равна площадипрямоугольникасосторонами, равнымиподлинеабсциссеиординате этой точки.
Решение
Уравнение MT имеет вид Y − y = y'( X − x) ; Y = 0 − y = y'( X −
|
y |
|
|
y |
|
|
− x) X = x − |
|
|
x − |
|
; 0 |
|
|
|
|||||
y' |
. Тогда точка T |
y' |
. |
|||
|
|
|
|
|
139

Решебник задач по теме "Дифференциальные уравнения"
y Уравнение ML имеет вид Y − y =
Уравнение ML имеет вид Y − y =
|
|
= |
−1 |
( X − x); Y = 0 −y |
= − |
1 |
( X − x) |
||||||||
|
|
|
|
||||||||||||
|
M (x, y) |
|
y′ |
|
y' |
||||||||||
|
X = x + yy′ ; L(x + yy′; 0) . |
||||||||||||||
|
|
||||||||||||||
O L |
T |
x |
Расстояния: |
|
ML |
|
= |
(x + yy′ − x)2 + y2 = |
|||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
= y 1+ y′2 (рассматриваем y > 0); |
|
MT |
|
= |
|||||||||
|
|
|
|
||||||||||||
|
|
|
y |
2 |
|
|
|
|
x − |
+ y2 = y 1 + y′2. |
|||||
= |
|
|
− x |
||||
|
|
|
y′ |
|
y′ |
||
|
|
|
|
||||
По условию ML MT = xy или y (1+ y′2 ) = xy′ . Дифференциальноеуравнениерешаемподстановкойy' = p:
|
|
|
|
|
|
|
|
|
y + p2y – xp = 0. |
|
|
|
|
|
|
||||||||||
Дифференцируем(1) пох: y′ + 2 py |
dp |
|
+ p2 y′ − p |
− x |
dp |
= 0 |
|||||||||||||||||||
dx |
dx |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 py dp + p3 = x dp |
|
p3 = dp |
(x − 2 py) . Из (1) |
|
|
|
|
|
|
||||||||||||||||
dx |
|
|
dx |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
y = |
|
xp |
|
. |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1+ p2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
dp |
|
|
2xp |
|
|
|
(1 − p2 )x |
|
dp |
|
|
|
|
|||||||||
Тогда |
p3 |
= |
|
|
x − |
|
|
|
p3 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||
|
|
|
dx |
|
|
1 + p |
|
|
|
|
|
1 + p |
|
|
dx |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
(1)
(2)
1 − p2 |
|
|
|
dx |
1 − p2 |
|
A B R Dp + K |
|
|
|
|
|
|||||||||||||||||||||||
p3 (1 + p2 ) dp = |
|
|
|
; |
p3 (1 + p2 )= |
|
|
+ |
|
|
+ |
|
|
|
|
|
+ |
|
|
|
A = 1, B = 0, |
||||||||||||||
x |
|
|
p3 |
p2 |
p |
1 + p2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
+ ln (1 + p2 ); |
|
C1xp2 |
|
= |
||||||||||||||
R = −2, K = 0, D =1 |
ln |
|
C x |
|
= − |
|
|
− 2ln |
|
p |
|
ln |
|
||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
1+ p2 |
|||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
= − |
1 |
|
|
C1xp2 |
|
= e−1/ 2 p2 x = |
Ce−1/ 2 p2 (1 + p2 ). |
|
|
|
|
|
|||||||||||||||||||||||
2 p2 |
1 + p2 |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
140
