Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет кораблестроения им. адм. Макарова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Kuznecov_reshebnik

.pdf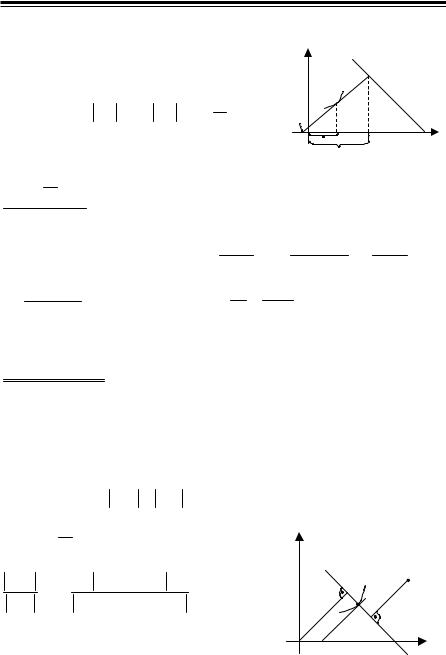

Скачиваний:

1096

Добавлен:

15.02.2015

Размер:

4.95 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 3212 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Уравнения первого порядка

Решение

y = 2 ;

(1)

М(х, у)

y = ax + b

X = x + PN = x + KP = x + y′ .

(2)

Подставив (2) в (1), получим

a x

+ b

y′

= 2

axy′ + ay

+ by′ = 2 y y′

(2 y − b − ax) y′ = ay ;

2 y − b − ax = z , 2 y′ − a = z′

y′ = z′ + a ;

y = z + b + ax ;

z′ + a

= a z + b + ax

z dz = (a2 x + ba) dx ; z2

= a2 x2

+ abx + C

;

= a

+ 2 abx + C2; 4 y2 + b2 + a2 x2 − 4by − 4ax y + 2abx = a2 x2 + 2abx + C2

y2 − by − axy = C , где

C = C – b2.

191 (4091). Найти линию, для которой отношение расстояния от нор-

мали в любой ее точке до начала координат к расстоянию от той же

нормали до точки (a; b) равно постоянному k.

Решение

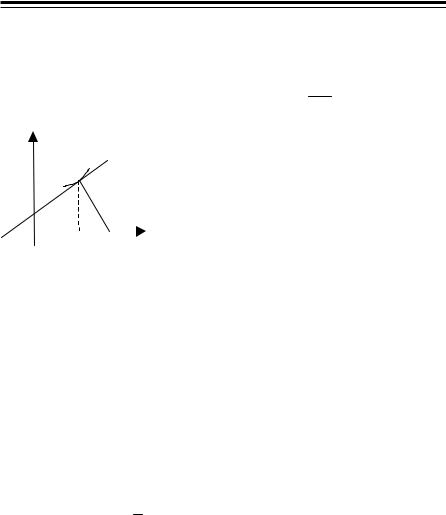
По условию

ON = LK k . Уравнение нормали NL имеет вид

Y − y = −

( X − x)

(Y − y) y′ + ( X − x) = 0; у

y′

= k;

− ( y y′ + x)

= k .

N М(х, у) K (a, b)

(b − y) y′ + (a − x)

Исходя из определения модуля числа,

рассмотрим два случая:

111

Решебник задач по теме "Дифференциальные уравнения"

− ( y y′ + x)

а)

= k

(b − y) y′ + (a − x)

[k b + (1 − k) y ] y′ + (1 − k) x + k a = 0;

(1)

k b + (1 – k) y = z, (1 – k) y' = z', y′ =

z′

z z′

+ (1 − k) x + k a = 0.

− k

1 − k

Обозначим z2 = W , 2zz′ =W ′ ,

W ′

= (k −1) x − k a ∫ dW

2 (1 − k)

= ∫ (− 2 (k −1)2 x + 2 (k −1) ka)dx

W = − (k −1)2 x2 + 2(k −1) kax +

+ C

= z2

;

k 2b2

+ 2kb (1 − k) y + (1 − k)2 y2 = − (k −1)2 x2 + 2 (k −1) kax +

+ C

= z2

+ y2 −

2 k

(ax + by) = C (k ≠ 1).

k −1

б)

y y′ + x

= k

(b − y) y' + (a − x)

y′[k b − y (k +1) ] − (k +1) x + k a = 0;

(2)

k b − y (k +1) = z, − y′ (k +1) = z′, y′ = −

z′

, −

z z′

−

1 + k

k +1

Обозначим

z2 = W , 2zz′ =W

′ , −

′

= (1 + k)

2 (k +

= 2

∫

(k a

− (1 + k) x) (1 + k) dx + C1

; W = 2 kax − (1 + k)

+ C

= z2 ;

k 2 b2

− 2kby (1 + k) + y2 (1 + k)2 = 2ka (1 + k)

(1 + k) x + k a = 0.

x − k a ; ∫ dW =

x2 (1 + k) +

x − (1 + k) x +

+ C	x2 + y2 −	2 k	(ax + by) = C		(k ≠ −1) .
+ C	x2 + y2 −		(ax + by) = C		(k ≠ −1) .
1		k +1		1
		k +1

112

Уравнения первого порядка

Если в уравнении (1) положить k = 1, а в уравнении (2) k = –1, то получимодноитожедифференциальноеуравнение:

b y′ = −a y′ = − ba , y = − ba x + C или a x + b y = C (k = 1 или k = –1).

192 (4092). Найти линию, для которой расстояние от начала координат до касательной в произвольной ее точке равно расстоянию от начала координат до нормали в той же точке.

Решение

Уравнение касательной к кривой y = f (x) в точке M (x; y) будет

Y – y = y' (X – x) или y' (X – x) – (Y – y) = 0.

Уравнение нормали имеет вид

Y − y = − y1′ ( X − x) ; − ( X − x) − y′ (Y − y) = 0 .

Расстояние от точки О(0; 0) до касательной и нормали:

d	1	= − x y′ + y	; d	2	= x + y′y .
	1	y2 +1		2	y′2 +1
		y2 +1			y′2 +1

Так как d1 = d2 , то выражение под знаком модуля положительно:

–x y' + y = x + y' y,

(1)

− y′ +

= 1 + y′

= u ,

y = x u , y′ = u′ x + u , − u′x − u + u = 1 + u u′x +

+ u2

−

(1 + u) du

arctg u −

ln (1 + u2 ) = ln

1 + u2

arctg

y = ln

C x

x2 + y2

x2 + y2 = C e± arctg(y / x)

(знак плюс (+)

получитсяпридругихвариантахуравнения(1)); ρ = x2 + y2 ,

= tg ϕ

ρ = Ce± ϕ

– уравнениялогарифмическихспиралей.

113

Решебник задач по теме "Дифференциальные уравнения"

193 (4093). Найтилинию, обладающуюследующимсвойством: ордината любой ее точки есть средняя пропорциональная между абсциссой исуммойабсциссыиподнормали, проведеннойклиниивтойжеточке.

Решение

Поднормаль Прх MN = −PN = − y tg α =

= − y y′. По условию y2 = x (x – y y'). Тогда

М(х, у)

=1 −

y′ ,

= u , y′ = u′ x + u ;

u2 =1 − u′ u x − u2, 2 u2 −1 = −u′ u x

u du

2 u2 −1

−

= −4 ln

2 u2 −1

= 1+

y2 =

x4 + C 4

2 x2

194 (4094). В электрическую цепь с сопротивлением R = 3/2 Ом в течение двух минут равномерно вводится напряжение (от нуля до 120 В). Кроме того, автоматически вводится индуктивность, так что число, выражающее индуктивность цепи в генри, равно числу, выражающему ток в амперах. Найти зависимость тока от времени в течение первых двух минут опыта.

Решение

По условию R = 32 Ом; U0 = 0; U = 120 В; t = 2 мин = 120 с. Паде-


ниенапряжениявдольпроводника U = R I + L	dI	. ТакжепоусловиюI = L

	dt
(численно); значит, U = R I + I I ′ , U = k t, 120 = k 120			k = 1 и U = t.
Имеем следующее дифференциальное уравнение:
t = R I + I I'.			(1)

114

Уравнения первого порядка

	Ищем решение в виде
	I = At,	I' = A.							(2)
	Подставляем (2) в (1), учитывая, что R =		3	:
			2
3	At = t − A2t 2 A2 + 3 A − 2 = 0, A =	− 3 ± 9 +16			,	A > 0 ,	A =	1	,
2	At = t − A2t 2 A2 + 3 A − 2 = 0, A =	4			,	A > 0 ,	A =	2	,
2		4						2

I = 2t .

Решебник задач по теме "Дифференциальные уравнения"

§ 2. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА (продолжение)

Поле направлений. Изоклины

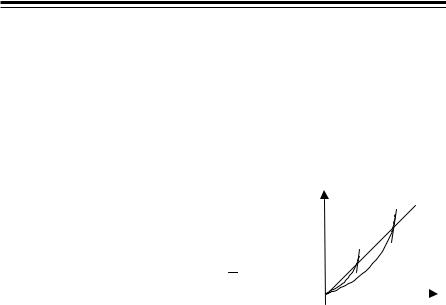
195 (4095). Данодифференциальноеуравнение y′ = − xy.

а) Построить поле направлений, устанавливаемое данным уравнением.

б) Выяснить расположение вектора поля относительно полярного радиуса любой точки поля.

в) Выяснить вид интегральных кривых уравнения исходя из поля направлений.

г) Найти интегральные кривые, решая данное уравнение обычным методом (разделяя переменные).

д) Указать семейство изоклин данного уравнения.

Решение

Изоклиной называется множество точек, в которых касательные к интегральным кривым имеют одно и то же направление.

Для дифференциального уравнения y′ = −

изоклинами будут

прямые:

k = 1 y

k = 2

k = – 1

−

= k

y = −

= −

x dx =

k = – 2

= −y dy;

x2 + y2 = C – семейство кон-

центрическихокружностей.

Вектор поля в каждой точке перпен-

дикуляренкполярномурадиусу точки.

196 (4096). Написать дифференциальное уравнение, изоклинами которого служат: 1) равнобочные гиперболы ху = а; 2) параболы y2 – 2px; 3) окружности x2 + y2 = R2.

116

Уравнения первого порядка (продолжение)

Решение

y′ = f (x

1) y′ = f (xy) ; 2) y′ = f

; 3)

+ y

197 (4097). Найти изоклины дифференциального уравнения семейства парабол y = ax2. Сделать чертеж. Истолковать результат геометрически.

Решение

Дифференцируемисходноеуравнениепох:

y' = 2ax.

(1) у

Подставляя в (1) значение а = у/х2 из уравнения семейства, получим дифференциальное

уравнениеданногосемейства: y′ = 2 xy. Изокли-

			y			k
			y	= k	y =	k		y = Cx	О	х
намибудутлинии 2							x или
намибудутлинии 2			x			2	x или
	k
C =		, т. е. прямые. Результат может быть высказан в форме теоре-
C =
	2

мы: если семейство парабол, имеющих общую ось и общую вершину, пересечь прямой, проходящей через вершину, то касательные к различным параболам в точках пересечения их с прямой будут между собой параллельны.

198 (4098). Убедиться, что изоклинами однородного уравнения (и только однородного уравнения) служат прямые, проходящие через начало координат.

Решение
	y
Общийвидоднородногоуравнения: y′ = f		.

	x

	y	y	= ϕ (k) = const = C , где
Уравнение изоклин k = f				y = Cx –

	x	x

семейство прямых, проходящих через начало координат.

117

Решебник задач по теме "Дифференциальные уравнения"

199 (4099). Указатьлинейныеуравнения, изоклинамикоторыхявляются прямые.

Решение
y′ = ay + b	k = ay + b	ay + b = kx – семейство прямых.
x	x

200 (4100). Пусть у1, у2, у3 – ординаты трех любых изоклин некоторого линейногоуравнения, соответствующиеоднойабсциссе. Убедиться, что

отношение y2 − y1 сохраняет одно и то же значение, какова бы не была y3 − y1

эта абсцисса.

Решение

Линейноеуравнение y′ + p (x) y = q (x) .

Уравнениеизоклины q (x) − p (x) y = C.

Рассмотрим три различные изоклины с ординатами у1, у2, у3, соответствующие одной абсциссе x:

q (x) − p (x) y1 = C1, q (x) − p (x) y2 = C2 , q (x) − p (x) y3 = C3


y	=	q(x) − C1			;

1				p(x)

y2	=			q(x) − C2		;
				p(x)

y3	=		q(x) − C3			;

				p(x)

y2		− y1	=	C1	− C2	= const .
		− y	=	C − C		= const .
y	3	− y		C − C
	3	1		1	3

Приближенное интегрирование дифференциальных уравнений

201 (4101). Дано уравнение y′ = x210+ y2 . Построить приближенно ин-

тегральную кривую, соответствующую отрезку 1 ≤ x ≤ 5 и проходящую через точку M (1; 1).

118

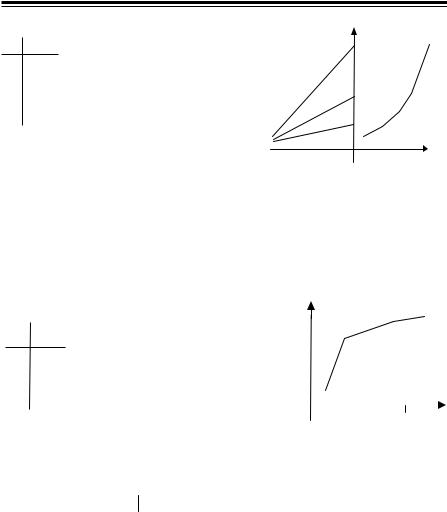
Уравнения первого порядка (продолжение)

Решение

y'i

+ y

M ′

f (x) =

; yi = yi−1 +

0,2

0,54

+ f (xi−1, yi−1)h, h = 1;

M ′2

1,30

y2 = 1 + 0,2 = 1,2; y3 = 1,2 +

2,52

+ 0,54 = 1,74; y4 = 1,74 + 1,30 = 3,04;

y5 = 3,04 + 2,52 = 5,56.

1 2

3 4 5

202 (4102). Дано уравнение y′ =

. Построить приближенно ин-

x2 + y2

тегральную кривую, соответствующую отрезку 0,5 ≤

x ≤

3,5 и проходя-

щую через точку (0,5; 0,5).

Решение

x [0,5; 3,5], h = 1, (0,5; 0,5);

y2 = 0,5 +

2 = 2,5; y3 = 2,5 +

0,5

1,5

0,13

+ 0,13 = 2,63; y4 = 2,63 + 0,08 =

2,5

0,08

= 2,71.

203 (4103). Дано уравнение y′ = xy3 + x2. Применяя способ Эйлера, вычислить y при x = 1, если y – частное решение, удовлетворяющее на-

чальному условию y x = 0 = 0 . Вычислить y с двумя десятичными знаками.

Решение

Программа вычислений на языке PASCAL:

Program Eler;

Function F(X, Y : Real) : Real; Begin

F := X*Sqr(Y)*Y + Sqr(X);

End;

119

Решебник задач по теме "Дифференциальные уравнения"

Const

X0: Real = 0;

XN: Real = 1;

Y0: Real = 0;

N=20;

Var

h:Real;

m : Integer;

X, Y : Array [0..N] Of Real;

Begin

X[0] := X0;

Y[0] := Y0;

h := (XN - X0)/N;

For m := 1 To N Do Begin

Y[m] := Y[m - 1] + h*F(X[m - l],Y[m - 1]);

X[m] := X0 + m*h;

End;

WriteLnf('x = ',X[N]:4:2,' y = ',Y[N]:4:2);

End.

x = 1.00 y = 0.31

204 (4104). Дано уравнение y′ = x y2 +1. Применяя способ Эйлера, вычислить y при x = 2, если y – частное решение, удовлетворяющее начальному условию y x = 0 = 0 . Вычислить y с двумя десятичными знаками.

Решение

По способу Эйлера yi = yi − 1 + f (xi −1, yi − 1)h. Вычислить y при

y'= x y2 +1; y x = 0 = 0 .

Программа вычислений на языке PASCAL:

Program Eler;

Function F(X, Y : Real) : Real; Begin

F := Sqrt(X)*Sqr(Y) + 1;

End;

Const

120

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 3212 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.02.2015249.86 Кб7Kursova_robota_pochti_gotovaya.doc
#
15.02.20151.24 Mб16Kursovoy_Sistemy.docx
#
09.12.2018274.43 Кб9kurs_9.doc
#
19.08.2019138.24 Кб1Kurs_lektsiy.doc
#
15.02.2015979.17 Кб19Kuznecov_Praktikum.pdf
#
15.02.20154.95 Mб1096Kuznecov_reshebnik.pdf
#
15.02.20158.28 Mб43Kvasnickij_Pajka_mat.pdf
#
14.02.2015755.2 Кб41Lab1_kl_metod.doc
#
14.02.20152.66 Mб34Lab2_KL_metod.doc
#
14.02.2015547.06 Кб26Laba_1.docx
#
14.02.2015177.15 Кб7Laba_2.doc