
3447
.pdf
обратил внимание на то, что численность населения растет в геометрической прогрессии an 1 kan , что в непрерывном
представлении соответствует закону (2.100). На основе эмпирических данных того времени Мальтус заметил, что производство продуктов питания растет со временем линейно (в арифметической прогрессии). Он был первым ученым, который на основе моделирования этих процессов предупреждал о возможных негативных последствиях определенных сценариев развития человеческого сообщества.
В 60-х годах ХХ века аналогичную роль сыграли работы представителей Римского клуба – Д. Форрестера (Мировая динамика, 1972 г.), Д. Медоуза (пределы роста, 1972 г., русский перевод 1991 г.), Д. Медоуза с соавторами (За пределами роста, 1992 г., русский перевод, 1994 г.). Дальнейшие исследования показали, что в природе экспоненциальный рост численности популяции встречается крайне редко, из-за ограниченности пищевых ресурсов и других альтернативных факторов. Примером выполнения экспоненциального закона (в ограниченный промежуток времени) может служить размножение видов, переместившихся в места с большими пищевыми ресурсами, где отсутствуют хищники и конкурирующие виды.
З а д а ч а о б о г р а н и ч е н н о м р о с т е п о п у л я ц и й1 . Рассмотрим еще одну классическую модель математической реологии. Логистическое уравнение было предложено в 1838 г. Ферхюльстом для описания ограниченного роста численности популяции. Оно имеет
следующий вид:
|
|
dy |
ky 1 |
|
y |
. |
|
(2.102) |
||
|
|
|
|
|
|
|||||
|
|
dt |
|
|
P |
|
|
|
||
Такое уравнение обладает двумя интересными для |
||||||||||
приложений |
свойствами; |
при |
малых |
t |
происходит |
рост |
||||
численности популяции; |
при больших |
t - численность y(t) |
||||||||
приближается к предельному значению |
P . Эта предельная |
|||||||||
величина, |
называемая |
емкостью |
экологической |
ниши |
||||||
|
|
|
|
80 |
|
|
|
|
|
|

популяции, такими факторами, как ограниченность пищевых и пространственных ресурсов и многими другими факторами, различными для разных видов. Мы докажем это свойство решения уравнения (2.102) на основе фактически построенного решения.
Разделяя переменные в уравнении, получим:
Pdy |
1 |
1 |
dy kdt, |
||
|
|
|
|
|
|
y(P y) |
|
y |
|
R y |
|
где выполнено разложение правильной рациональной дроби на сумму простейших дробей. Интегрируя дифференциальное уравнение, имеем:
ln |
|
y |
|
ln |
|
R y |
|
kt |
ln |
|
C |
|
, |
|
y |
|
|
Cekt |
, C 0. |
(2.103) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
y |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Постоянная C определяется начальным значением |
|||||||||||||||||||||
численности популяции |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
y(0) |
y0 , C |
|
|
|
y0 |
. |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
R y0 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Из общего интеграла (2.103), учитывая найденную константу, получим частное решение уравнения (2.102), удовлетворяющее начальному условию:
y(t) |
y0 Pekt |
|
|
|
. |
(2.104) |
|
P y0 y0ekt |
|||
Рассмотрим поведение численности |
популяции при |
||
kt 1. Разлагая экспоненту в степенной ряд и ограничившись двумя членами
ekt 1 kt,
запишем приближенно выражение в правой части (2.104) в виде
y0 Pe kt |
|
y0 P(1 kt) |
|
|
y0 |
|
(1 kt). |
|
P y0 (1 ekt ) |
|
P y0kt |
|
|
|
y0 |
|
|
|
1 |
|
kt |
|||||
|
|
P |
||||||
|
|
|
|
|||||
81
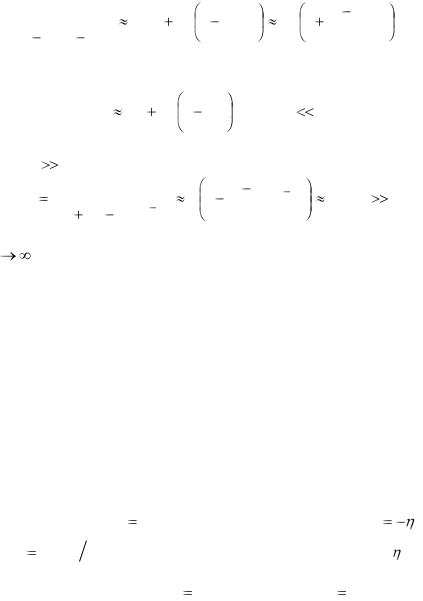
Разлагая дробь в правой части равенства в геометрический ряд и ограничиваясь членами первого порядка малости, имеем:
|
|
y0 Pekt |
|
|
y0 (1 |
kt) 1 |
|
|
y0 |
kt |
|
y0 1 |
|
P y0 |
kt . |
|||||||
|
P |
y0 (1 |
ekt ) |
|
|
|
P |
|
|
P |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Таким образом, при малых kt численность популяции |
|||||||||||||||||||||
возрастает линейно с ростом времени: |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
y(t) |
y0 |
y0 |
1 |
|
y0 |
|
kt, |
(kt |
1) . |
|
|||||||
|
|
|
|
|
|
P |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Рассмотрим теперь поведение решения уравнения (2.104) |
|||||||||||||||||||||
при kt |
|
1. Имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y(t) |
|
|
|
y0 P |
|
|
|
|
P 1 |
|
P y0 |
e |
kt |
|
P (kt 1). |
|||||||
|
y |
0 |
(P y |
0 |
)e |
kt |
|
|
y0 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Действительно, численность популяции стремиться при |
|||||||||||||||||||||
t |
к предельному значению, равному P . |
|
|
|
||||||||||||||||||
Отметим, что если хотя бы один из системных факторов k, P зависит от времени, то уравнение (2.102) не допускает
разделение переменных. Однако и в этом случае его решение выражается квадратурами, поскольку оно будет являться уравнением Бернулли.
З а д а ч а о п а д е н и и т е л а в г р а в и т а ц и о н н о м п о л е.
Рассмотрим задачу о вычислении скорости тела массы m , падающего вертикально вниз с некоторой высоты под действием силы тяжести, если сила вязкого трения, действующая на тело, пропорциональна величине скорости.
Обозначим v(t) - скорость тела в момент времени t . Действующие на тело две противоположно направленные силы
– сила |
тяжести FT |
mg и сила вязкого |
трения FTр |
v , |
где g |
9,81м с2 - |
ускорение свободного |
падения, |
- |
динамическая вязкость (пуаз=0,1Па∙с). Значение коэффициента вязкости для воздуха при T 293K и давлении p 101,3кПа ;
82

=0,018мПа∙с; для воды при T 293K : =1,002мПа∙с. Дифференциальное уравнение получаем из второго закона
Ньютона ma F |
FT |
FTр : |
|
|
|
|
||
m |
dv |
|
mg |
v , или |
dv |
|
|
v g . |
|
|
|
|
|||||
|
dt |
|
|
dt |
|
m |
||
Разделяя переменные и интегрируя, получаем:
dv
t C1 .
m v g
Вычисляем интеграл в левой части равенства методом подведения под дифференциал:
|
dv |
|
m |
|
d |
|
|
v g |
|
m |
|
|
|
|
|
||
|
|
m |
|
|
|
|
|
||||||||||
|
|
|
|
ln |
|
|
v g |
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
v g |
|
|
|
|
|
|
v g |
|
|
|
|
m |
|
||
|
m |
|
|
|
|
m |
|
|
|
|
|
|
|
||||
Учитывая правую часть предыдущего равенства, получаем:
|
m |
|
|
|
|
|
|
|
|
|
|
v g e |
|
|
C1 e |
|
t , |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
ln |
|
|
|
v g |
t C , |
|
|
m |
m |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
m |
|
|
|
1 |
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mg |
|
|
Ce |
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
C1 |
|
v(t) |
1 |
m |
|
, |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
mg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|||
где |
C e |
|
m |
, |
|
м с , |
|
|
|
|
|
|
|
|
1 с , |
- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
коэффициент |
|
|
затухания |
|
движения. |
|
При |
|
интегрировании |
|||||||||||||||||||||
уравнения мы не учитывали решение |
v |
|
mg |
|
|
const , |
как не |
|||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
имеющее физического смысла. Если тело начинает движение с нулевой начальной скоростью v(0) 0 , то C 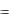 mg
mg 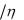 и решение примет вид
и решение примет вид
83

|
mg |
|
|
|
t . |
|
v(t) |
1 |
e |
m |
|||
|
||||||
При свободном падении |
без |
|
трения v(t) gt . При |
|||
наличии вязкого трения скорость, возрастает, стремиться к постоянной величине v mg  .
.
З а д а ч а о б и з м е н е н и и т е м п е р а т у р ы т е л а в с р е д е.
Тело, имеющее в начальный момент времени температуру T (0) T0 , поместили в среду, температура которой
поддерживается неизменной и равной Tc (термостат). Рассмотрим закон изменения температуры тела со временем, если Tc T0 .
Обозначим T(t) температуру тела в момент времени t . И.
Ньютон экспериментально установил закон, согласно которому при определенных упрощениях скорость изменения температуры тела пропорциональна разности температур тела и окружающей среды
|
|
|
|
dT(t) |
(T (t) Tc ) , |
T (0) |
T0 , |
|
|
|
|
|
|
|
|
||||
|
|
|
|
dt |
|
||||
|
|
|
|
|
|
|
|
|
|
где |
0 - постоянная. Знак минус в правой части уравнения |
||||||||
соответствует |
|
экспериментальным |
результатам: |
если |
|||||
T (t) |
Tc |
0 , |
то температура тела убывает, |
поэтому скорость |
|||||
ее изменения отрицательна: T (t) |
Tc |
0 , то температура тела |
|||||||
возрастает, |
поэтому и dT dt |
0. Таким |
образом, |
процесс |
|||||
охлаждения (нагревания) тела моделируется приведенным уравнением, которое является линейным дифференциальным уравнением первого порядка. (Очевидно, что его можно
решить и методом разделения переменных при Tc |
const). |
Будем отыскивать решение уравнения методом Бернулли: |
|
T(t) u v . Подставляя это произведение в |
уравнение, |
84
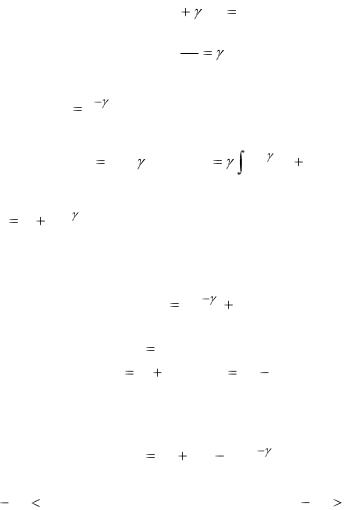
привлекая условие Бернулли, налагаемое на одну из функций, получаем систему двух дифференциальных уравнений:
dv(t) |
v(t) 0, |
|
|
||
dt |
||
|
du
v(t) dt Tc .
Интегрируя первое уравнение системы, находим частное решение v(t) e t . Из второго уравнения получаем функцию u(t) :
du |
1 |
T dt , |
u |
T e t dt C. |
|
||||
|
||||
|
v(t) |
c |
|
c |
|
|
|
|
|
Для постоянной |
температуры |
внешней среды, имеем: |
||
u(t) C T0e t .
Таким образом, общее решение дифференциального уравнения, описывающего изменение температуры тела, имеет вид:
|
T (t) Ce |
t |
Tc . |
|
|
||
Для нахождения |
значения |
параметра C используем |
|
начальное условие T (0) T0 . Имеем: |
|
||
T0 |
C Tc , |
C T0 Tc . |
|
Подставляя найденное значение параметра в общее решение уравнения, находим искомую зависимость температуры тела от времени
|
T (t) |
T (T T )e |
t . |
|
||
|
|
c |
0 |
c |
|
|
Отсюда |
видим, что |
функция T(t) |
возрастает, если |
|||
T0 Tc 0 , т.е. тело нагревается. Если же T0 |
Tc 0 , то тело |
|||||
охлаждается, |
так как функция T(t) |
убывает. В обоих случаях с |
||||
возрастанием |
t значение |
функции T(t) |
приближается к Tc , |
|||
что физически очевидно.
З а д а ч а |
о т е м п е р а т у р е ц и л и н д р и ч е к о й |
к а т у ш к и с |
т о к о м. |
85

Пусть через цилиндрическую катушку, изготовленную из медной проволоки, протекает электрический ток. При этом, как известно из курса физики, в проводнике выделяется тепло Джоуля-Ленца. Получим формулу временной зависимости температуры цилиндра T(t) , учитывающую теплообмен с
окружающей средой.
Введем обозначения: s - площадь поверхности катушки; V - объем катушки; 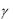 - удельный вес меди; c - ее удельная
- удельный вес меди; c - ее удельная
теплоемкость; k - коэффициент теплопроводности; T0 - температура среды, в которую помещена катушка с током; q -
количество теплоты, выделяемой в единицу времени током в проводнике (тепло Джоуля-Ленца).
Количество теплоты, выделяющееся за время t , будет равно Q q  t . Эту величину можно записать исходя из соотношения баланса в виде суммы
t . Эту величину можно записать исходя из соотношения баланса в виде суммы
Q Q1 Q2 ,
где Q1 - тепло, расходуемое на повышение температуры проводника T , Q2 - тепло, расходуемое на повышение
температуры среды (уходящее тепло). Из курса физики известно:
|
|
Q1 |
cV T , |
|
Q2 |
ks(T T0 ) t , |
|
||||||
где T - температура проводника. |
|
|
|
|
|||||||||
Теперь уравнение баланса можно записать в виде: |
|||||||||||||
|
|
|
|
q t cV T ks(T T0 ) t |
|
|
|||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
cV |
|
T |
ks(T T0 ) . |
|
|
|||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
t |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Переходя |
к |
пределу |
при |
t |
0 |
и |
учитывая |
||||||
lim |
T |
T (t) , |
получаем |
дифференциальное |
уравнение, |
||||||||
|
|||||||||||||
t |
|||||||||||||
t 0 |
|
|
|
|
|
|
|
|
|
|
|
||
моделирующее описанный процесс, в виде: |
|
|
|||||||||||
|
|
cV |
dT(t) |
ks(T (t) |
T ) |
q, |
T (0) |
T . |
|
||||
|
|
|
|
||||||||||
|
|
|
|
dt |
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
86
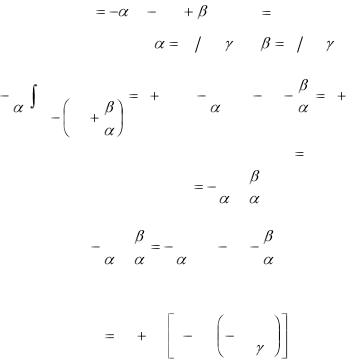
Отсюда
|
|
|
|
dT |
|
|
|
|
(T |
|
T0 ) |
, |
|
T (0) |
|
|
T0 , |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
dt |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где введены обозначения: |
|
|
|
ks (cV ) , |
|
|
|
|
q (cV ) . |
|||||||||||||||||||||||
Разделяя переменные и интегрируя, получим |
|
|||||||||||||||||||||||||||||||
1 |
|
|
dT |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
t C . |
||||||
|
|
|
|
|
|
|
t C, |
|
|
ln |
T T |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||||
|
|
|
T |
T0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Используя |
начальное |
|
условие |
T (0) T0 , |
найдем |
|||||||||||||||||||||||||||
постоянную интегрирования: |
|
C |
|
|
|
1 |
ln |
|
. |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
. |
|
|
|
||||||||
|
|
|
|
t |
|
ln |
|
|
|
|
ln |
T |
|
T |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||
Отсюда, раскрывая модуль в правой части равенства, |
||||||||||||||||||||||||||||||||
найдем функцию T(t) : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
T (t) T |
|
q |
1 |
|
exp |
|
|
|
|
ks |
|
|
t . |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
0 |
|
|
ks |
|
|
|
|
|
|
|
|
|
|
cV |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для конкретизации полученной зависимости необходимо задать объем и площадь поверхности цилиндра, длину проводника и силу тока в проводнике (для формулы ДжоуляЛенца). Остальные величины можно найти в справочнике по физике.
З а д а ч а г и д р а в л и к и о т е ч е н и и ж и д к о с т и в т р у б е.
Пусть в прямолинейной цилиндрической трубе радиуса R течет жидкость. Предположим, что в результате трения жидкости о стенки трубы скорость каждого цилиндрического слоя жидкости уменьшается при увеличении расстояния слоя от оси цилиндра. Задача заключается в определении скорости слоя v как функции расстояния r до оси цилиндра.
Из гидравлики известно, что зависимость между скоростью и расстоянием слоя до оси выражается уравнением
87
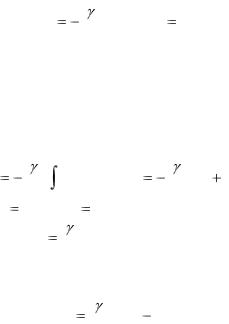
dv |
|
i |
r , |
v(R) 0 , |
dr |
|
2E |
||
|
|
|
где  - удельный вес жидкости; E - коэффициент упругости;
- удельный вес жидкости; E - коэффициент упругости;
i - гидравлический спад. Знак “минус” в уравнении обусловлен тем, что с увеличением r скорость течения уменьшается. Начальное условие означает прилипание жидкости к стенкам трубы в силу вязкости жидкости.
Разделяя переменные и интегрируя, имеем:
v |
i |
rdr, |
|
v(r) |
|
i |
r 2 |
C. |
|
||
|
|
|
|
|
|||||||
|
2E |
|
|
|
|
|
4E |
|
|
||
Полагая r |
R |
и v |
0 , |
найдем |
значение |
постоянной |
|||||
интегрирования |
C |
|
i |
|
R2 . |
Таким |
образом, |
полученная |
|||
|
4E |
||||||||||
|
|
|
|
|
|
|
|
|
|
||
зависимость скорости слоев жидкости от расстояния до оси трубы имеет вид:
v(r) |
i |
(R2 |
r 2 ). |
|
4E |
||||
|
|
|
Вопросы для самоконтроля
1.Дайте определения дифференциального уравнения первого порядка, его общего и частного решений, общего и частного интеграла. Сформулируйте задачу Коши для дифференциального уравнения первого порядка, укажите ее геометрический и механический смысл.
2.Дайте геометрическую интерпретацию дифференциального уравнения первого порядка. Укажите геометрический смысл общего и частного решения.
3.Дайте определение дифференциального уравнения с разделяющимися переменными. Изложите метод построения его общего решения. Приведите пример.
4.Дайте определение однородного дифференциального уравнения первого порядка. Изложите метод нахождения его общего решения. Приведите пример.
88

5.Дайте определение линейного дифференциального уравнения первого порядка. Изложите метод нахождения его общего решения. Приведите пример
6.Дайте определение уравнения Бернулли. Изложите метод нахождения его общего решения. Приведите пример.
7.Дайте определение дифференциального уравнения в полных дифференциалах. Изложите метод нахождения его общего решения. Приведите пример. Как вводится понятие интегрирующего множителя уравнения?
8.Какое решение дифференциального уравнения называется особым решением?
|
|
|
|
Задачи для практических занятий |
|
|
|
|||||||||||||
1. |
xy |
y |
0. |
|
Ответ: y Cx, |
|
y |
|
|
2x. |
|
|
|
|||||||
2. |
xy |
y |
0. |
|
Ответ: xy C, |
|
|
xy |
8. |
|
|
|
||||||||
3. |
yy |
x |
0. |
|
Ответ: |
x2 |
y 2 |
|
|
C 2 , |
x2 |
y 2 20. |
||||||||
4. |
y |
y. |
|
|
|
Ответ: |
y |
Ce x , |
|
y |
4e x |
2. |
|
|
||||||
5. |
x 2 y |
y |
0. |
|
Ответ: |
y |
|
Ce1/ x . |
|
|
|
|
||||||||
6. |
x |
xy |
y ( y |
xy) |
0. Ответ: |
x |
y |
|
lnC(x |
1)(y |
1). |
|||||||||
7. |
(1 |
y2 )dx |
(1 |
x2 )dy . Ответ: y |
|
C |
|
x |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 |
|
Cx. |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
8. |
y |
xy |
1 |
x 2 y . |
Ответ: |
y |
1 |
|
Cx |
. |
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
x |
|
|
|
|
||
9. |
(xy2 |
x)dx ( y |
x2 y)dy |
0. Ответ: |
1 |
|
y2 |
C(1 x2 ) . |
||||||||||||
10. (1 |
2 y)xdx |
(1 |
x2 )dy |
0. Ответ: |
y |
|
|
|
|
C |
|
1 |
. |
|||||||
|
|
2(1 |
x2 ) |
|
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
11. xy(1 |
x2 ) y |
1 |
y2 . |
Ответ: (1 |
|
y2 )(1 |
x2 ) Cx2 . |
|||||||||||||
12. e y (1 |
x2 )dy |
2x(1 e y )dx |
0. Ответ: 1 |
|
e y |
C(1 |
|
x2 ). |
||||||||||||
89
