
3447
.pdf
2. |
y |
|
|
ln x |
, y(1) |
0, |
|
y (1) |
|
1, y (1) |
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
y |
|
|
|
|
|
|
|
x |
2 |
ln |
2 |
x |
|
|
3 |
|
x |
2 |
|
|
|
2x |
|
|
|
|
1 |
. |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3. |
|
y |
x |
cosx. |
|
|
|
|
|
Ответ: |
y |
|
|
x4 |
sin x |
|
C x2 |
|
|
|
C |
|
|
|
x |
|
|
|
C |
|
. |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4. |
|
y |
2x ln x. |
|
|
|
|
|
|
Ответ: |
y |
|
|
x3 |
ln x |
5 |
x3 |
|
C x |
|
|
|
C |
|
|
. |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5. |
x ln x y |
|
|
|
y . |
|
|
|
|
|
|
Ответ: |
y |
|
|
|
(C x |
C |
2 )eC1 |
|
|
|
C |
2 |
. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
6. |
xy |
|
y . |
|
|
|
|
|
|
|
|
|
|
Ответ: |
y |
|
|
|
|
|
C x2 |
|
|
C |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
7. xy |
(1 |
2x2 ) y . |
|
|
|
|
|
|
Ответ: |
y |
|
|
|
|
|
C e x 2 |
|
|
|
C |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
8. |
xy |
|
y ln |
. |
|
|
|
|
|
|
|
Ответ: |
y |
|
|
|
|
(C x |
C 2 )e C1 |
|
|
|
|
C |
|
|
. |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
9. 2 y |
|
y |
|
|
|
, y(1) |
|
|
|
2 |
, |
y (1) |
|
|
2 |
|
. |
|
|
|
|
Ответ: |
|
|
y |
|
|
|
|
|
|
2 |
|
|
x5 2 . |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
y |
|
|
|
|
|
|
5 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
( y )2 . |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
(C x |
|
|
|
C |
2 |
)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
10. 2yy |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
Ответ: y |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
11. |
y |
|
2y3, |
y(0) |
1, |
|
y (0) |
|
1. |
|
|
|
|
|
Ответ: |
|
|
|
y |
|
|
|
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
12. |
2yy |
y 2 |
y 4 |
|
|
4, |
|
y(0) |
1, |
y (0) |
|
|
|
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
5 |
|
|
|
|
3 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
1 |
|
|
|
x |
C2 |
|
общий интеграл. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Ответ: |
15 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
1 |
(15x |
1)2 3 |
|
4 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
13. |
yy |
|
|
y 2 |
|
|
y2 ln y (считая y |
|
|
0, y |
0) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
130

C1 ln2
Ответ:
y exp
14.y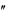 y (1 y ) .
y (1 y ) .
15.yy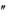 y (1 y ).
y (1 y ).
y C22e2x |
2C2 e x ln y |
|
ln2 y |
или |
|||||
C 2e2x |
C |
|
|
|
|
|
|
|
|
2 |
1 |
. |
|
|
|
|
|
|
|
2C2 e x |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
Ответ: |
y |
C2 |
ln1 |
|
exp(x |
C1) |
. |
||
Ответ: |
y |
1 |
(1 C |
|
eC1x ) . |
|
|
||
|
C1 |
2 |
|
|
|||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
16. |
yy |
1 |
y |
2 |
. |
Ответ: |
y C ch |
x |
C2 |
. |
|
|||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
17. |
y |
3yy , |
|
y(0) |
y (0) 1, y (0) |
3 |
. |
Ответ: |
y |
|
|
4 |
. |
|
|
2 |
|
(x 2)2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
4. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
4.1. Линейные дифференциальные уравнения второго порядка
Линейные дифференциальные уравнения второго порядка в теории дифференциальных уравнений занимают важное место не только потому, что представляют собой простой и хорошо изученный тип уравнений, но и потому, что многие практические задачи физики, механики, техники и особенно электротехники приводят к решению этих уравнений.
1. Основные понятия.
Определение. Уравнение вида
y p(x) y |
q(x) y f (x), |
(4.1) |
|
где y искомая функция, а |
p(x) , q(x) |
и f (x) |
непрерывные |
функции на некотором интервале (a,b) |
, называется линейным |
||
дифференциальным уравнением второго порядка.
Если f (x) 0, то уравнение (4.1) называется линейным однородным уравнением. Если же f (x) 0, то уравнение (4.1)
называется линейным неоднородным уравнением.
131

2. Линейные однородные дифференциальные уравнения второго порядка. Рассмотрим некоторые свойства решений линейных однородных уравнений.
Теорема |
1. |
Если |
функции |
y1(x) и |
y2 (x) |
решения |
||
уравнения |
|
|
|
|
|
|
|
|
|
|
y |
p(x) y q(x) y |
0, |
|
|
(4.2) |
|
то функция |
y |
C1 y1(x) C2 y2 (x) |
при |
любых |
значениях |
|||
постоянных C1 и C2 |
также является решением, уравнения |
|||||||
(4.2). |
|
|
|
|
|
|
|
|
Итак, |
функция |
вида |
y |
C1 y1(x) C2 y2 (x) |
с |
|||
произвольными постоянными C1 , |
и |
C2 |
является |
решением |
||||
уравнения (4.2). Естественно возникает вопрос, не является ли это решение общим решением уравнения (4.2). Покажем, что при некоторых условиях функция y C1 y1(x) C2 y2 (x)
является общим решением уравнения (4.2). Предварительно введем понятия линейной зависимости и линейной
независимости функций y1(x) |
и y2 (x) . |
|
|
|
|
|
|
|
||||||||||
|
|
Функции y1(x) и y2 (x) |
называются линейно зависимыми |
|||||||||||||||
на (а, b), если существуют такие числа 1 |
и |
2 , |
из которых |
|||||||||||||||
хотя бы одно отлично от нуля, что для любого x |
(a, b) имеет |
|||||||||||||||||
место равенство |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 y1(x) |
2 y2 (x) |
0 . |
|
|
|
|
(4.3) |
|||
|
|
Очевидно, что если функции |
y1(x) |
и |
y2 (x) линейно |
|||||||||||||
зависимы, |
то они пропорциональны. |
Действительно, |
если |
|||||||||||||||
|
1 y1(x) |
2 y2 (x) |
0, |
причем |
1 |
0 |
и |
y2 (x) |
0, |
|
то |
|||||||
|
y1(x) |
|
|
2 |
|
const . Верно и обратное. |
|
|
|
|
|
|
||||||
|
y2 (x) |
1 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Функции |
|
y1(x) и |
y2 (x) |
называются линейно |
||||||||||||
независимыми на (а, b), если не существует таких чисел |
1 |
и |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 , |
из которых хоть одно отлично от нуля, |
что для любого |
||||||||||||||||
|
x |
(a, b) |
имеет |
место |
равенство |
(4.3). |
Другими |
словами, |
||||||||||
132

равенство |
(4.3) |
выполняется |
сразу |
для всех |
x |
(a, b) , если |
||||||||||||||
только |
1 |
2 |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Очевидно, |
что |
|
если функции |
y1(x) и |
y2 (x) |
линейно |
|||||||||||||
независимы, то |
их |
|
отношение |
y1 |
(x) |
const |
, |
т. е. |
они |
не |
||||||||||
|
y2 |
(x) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
пропорциональны. |
Так, |
например, функции |
|
y (x) |
x2 |
и |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
y2 (x) x3 |
линейно независимы на любом интервале (а, |
b), |
|||||||||||||||||
поскольку |
|
y1(x) |
|
1 |
|
const , а |
функции |
y (x) |
|
4x2 |
и |
|||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
y2 (x) |
|
x |
|
|
|
|
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
y2 (x) x2 линейно зависимы на любом промежутке, так как |
|
||||||||||||||||||
|
y1(x) |
|
4 |
const . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
y2 (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Предположим |
|
теперь, |
что функции y1(x) |
и |
y2 (x) |
||||||||||||||
являются решениями уравнения (4.2). Вопрос о том, являются ли они линейно зависимыми или линейно независимыми,
решают с помощью определителя Вронского:
|
y1 |
y2 |
y1 y2 |
y2 y1. |
(4.4) |
|
y1 |
y2 |
|||
|
|
|
|
||
Определитель Вронского |
(или вронскиан) |
является |
|||
функцией, определенной на (а, b), и обозначается W ( y1, y2 ) или просто W(x).
Теорема 2. Если функции y1(x) и y2 (x) линейно
зависимы на (а, b), то определитель Вронского, составленный из них, равен нулю на этом интервале.
Теорема 3. Если решения y1(x) и y2 (x) уравнения (4.2)
линейно независимы на (а, b), то определитель Вронского, составленный из них, отличен от нуля на этом интервале.
Итак, установлено, что если функции y1(x) и y2 (x)
являются на (а,b) решениями линейного однородного уравнения (4.2), то составленный из них определитель
133

Вронского на (а, |
b) либо равен нулю ( y1(x) и |
y2 (x) |
линейно |
|||||
зависимы), |
либо |
отличен |
от нуля ( y1(x) и |
y2 (x) |
линейно |
|||
независимы). |
|
|
|
|
|
|
||
Установим |
теперь, |
при |
каких |
условиях |
функция |
|||
y C1 y1(x) |
C2 y2 (x) является |
общим |
решением линейного |
|||||
однородного уравнения (4.2). |
|
|
|
|
||||
Теорема 4. Если функции |
y1(x) и y2 (x) |
линейно неза- |
||||||
висимые на (а, b) |
решения уравнения (4.2), то функция |
|
||||||
|
|
|
y C1 y1(x) |
C2 y2 (x) |
|
|
(4.5) |
|
где C1 |
и |
C2 |
произвольные постоянные, является общим |
|||||
решением уравнения (4.2). |
|
|
|
|
|
|||
Из |
этой теоремы следует, что для отыскания |
общего |
||||||
решения уравнения (4.2) достаточно найти два линейно независимых частных решения и составить выражение (4.2) с произвольными постоянными C1 и C2 .
3. Линейные неоднородные дифференциальные уравнения второго порядка. Рассмотрим теперь основные свойства решений линейного неоднородного дифференциального уравнения второго порядка (4.1):
y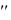 p(x) y
p(x) y q(x) y
q(x) y  f (x).
f (x).
Имеет место следующая теорема.
Теорема 5. Общее решение уравнения (4.1) есть сумма любого его частного решения и общего решения соответствующего однородного уравнения.
Таким образом, чтобы найти общее решение линейного неоднородного уравнения, нужно найти общее решение соответствующего однородного уравнения и какое-нибудь частное решение неоднородного уравнения. В общем случае задача отыскания частного решения является сложной. Покажем, как можно найти частное решение неоднородного уравнения методом вариации произвольных постоянных, если известно общее решение соответствующего однородного уравнения.
134

Пусть Y C1 y1(x) C2 y2 (x) 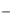 общее решение однородного уравнения (4.2). Будем искать частное решение неоднородного уравнения (4.1) в виде
общее решение однородного уравнения (4.2). Будем искать частное решение неоднородного уравнения (4.1) в виде
|
y |
C1(x) y1(x) |
C2 (x) y2 (x), |
|
(4.6) |
рассматривая C1 |
и C2 как некоторые искомые функции от х. |
||||
Продифференцируем последнее равенство |
|
|
|||
y C1(x) y1(x) |
С1(x) y1(x) |
C2 (x) y2 (x) C2 (x) y2 (x) . |
(4.7) |
||
Подберем |
функции C1(x) и C2 (x) |
так, |
чтобы |
||
выполнялось равенство |
|
|
|
||
|
C1(x) y1(x) C2 (x) y2 (x) 0 . |
|
(4.8) |
||
Тогда равенство (4.7) принимает вид |
|
|
|||
y С1(x) y1(x) C2 (x) y2 (x).
С1(x) y1(x) C2 (x) y2 (x).
Дифференцируя это равенство, найдем у":
y C1(x) y1(x) С1(x) y1(x) C2 (x) y2 (x) C2 (x) y2 (x).
C1(x) y1(x) С1(x) y1(x) C2 (x) y2 (x) C2 (x) y2 (x).
Подставляя выражения для у, у' и у" в уравнение (4.1) и группируя слагаемые, получаем
C1(x) y1(x) |
p(x) y1(x) q(x) y1(x) |
C2 (x) y2 (x) |
p(x) y2 (x) q(x) y2 (x) |
C1(x)(x) y1(x) C2 (x) y2 (x) 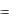 f (x).
f (x).
Выражения в квадратных скобках равны нулю, так как y1(x) и y2 (x)  решения однородного уравнения. Поэтому последнее равенство принимает вид
решения однородного уравнения. Поэтому последнее равенство принимает вид
C1(x) y1(x) C2 (x) y2 (x) f (x) . |
(4.9) |
Таким образом, функция (4.6) является решением |
|
уравнения (4.1), если функции C1(x) и C2 (x) |
удовлетворяют |
уравнениям (4.8) и (4.9). Объединяя их, получаем систему уравнений
С1(x) y1(x) |
C2 (x) y2 (x) |
0, |
(4.10) |
|
C1(x) y1(x) |
C2 (x) y2 (x) |
f (x), |
||
|
135

в которой С1(x) и С2 (x) |
неизвестны, а y1(x), y2 (x), |
y1(x), y2 (x) и f (x) 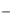 известны. Так как определителем этой системы является определитель Вронского
известны. Так как определителем этой системы является определитель Вронского
W (x) |
y1(x) |
y2 (x) |
, |
y1(x) |
y2 (x) |
составленный из линейно независимых решений y1(x) и y2 (x)
однородного уравнения (4.2), то он по теореме 5 не равен нулю, а значит, система (4.10) имеет единственное решение относительно С1(x) и С2 (x) . Решая эту систему, получаем
С1(x) 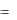 1(x), С2 (x)
1(x), С2 (x)  2 (x), где 1(x) и 2 (x)
2 (x), где 1(x) и 2 (x)  известные функции, откуда, интегрируя, найдем C1(x) и C2 (x) .Под-
известные функции, откуда, интегрируя, найдем C1(x) и C2 (x) .Под-
ставляя полученные выражения для C1(x) и C2 (x) в равенство (4.6), получаем искомое частное решение уравнения (4.1).
Пример. Найти частное решение уравнения у" у = х. |
||
Решение. Общее решение соответствующего однородного |
||
уравнения y y 0 имеет вид Y (x) C ex |
C |
e x . Поэтому |
1 |
2 |
|
частное решение неоднородного уравнения будем искать в виде
|
~ |
|
x |
C2 (x)e |
|
x |
. |
|
(4.11) |
|||
|
y (x) C1(x)e |
|
|
|
|
|||||||
Система (4.10) для нахождения С1(x) и С2 (x) в данном |
||||||||||||
|
С ( x)e x |
C |
2 |
( x)e x |
|
0, |
|
|
|
|
|
|
случае имеет вид |
1 |
|
|
|
|
|
|
|
|
|
|
|
C ( x)e x |
|
|
( x)e x |
|
|
|
|
|
|
|
|
|
|
C |
2 |
|
x. |
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Складывая эти уравнения, |
найдем |
С (x) |
1 |
xe |
x . |
|||||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда, интегрируя, получаем |
|
С (x) |
|
|
1 |
(x |
1)e x . |
|
|
|
||
|
|
|
|
|
|
|
||||||
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Произвольную постоянную не пишем, так как ищем |
||||||||||||
какое-нибудь частное решение. Подставляя выражение С1(x) |
в |
|||||||||||
136
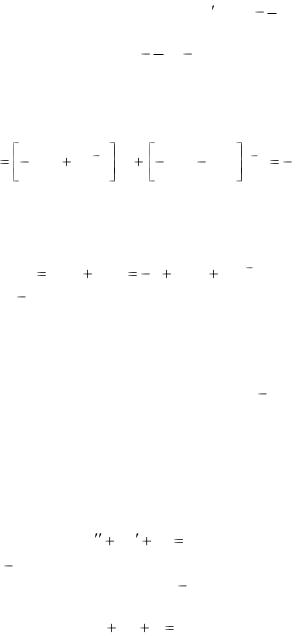
первое из уравнений системы, найдем С2 (x) 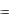 12 xex , откуда,
12 xex , откуда,
интегрируя, получаем С2 (x) 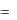 12 (x 1)ex .
12 (x 1)ex .
Подставляя |
найденные |
выражения C1(x) |
и |
C2 (x) в |
|||||||||||
равенство |
(4.11), |
получаем |
частное решение |
~ |
данного |
||||||||||
y |
|||||||||||||||
неоднородного уравнения: |
|
|
|
|
|
|
|
|
|
|
|||||
~ |
1 |
|
|
x |
|
x |
1 |
|
x |
|
x |
|
|
||
y |
|
|
(x 1)e |
|
e |
|
|
|
(x 1)e |
|
e |
|
|
x. |
|
|
2 |
|
|
|
2 |
|
|
|
|||||||
Заметим, что, найдя частное решение неоднородного уравнения и зная общее решение соответствующего однородного уравнения, на основании теоремы 5 можно записать общее решение данного неоднородного уравнения:
~ |
x C1e |
x |
C2e |
x |
, |
y y (x) Y (x) |
|
|
|||
где C1 и C2 произвольные постоянные. |
|
|
|
||
4.2. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Рассмотрим важный частный случай линейных дифференциальных уравнений второго порядка случай, когда функции р(х) и q(x) являются постоянными величинами. Такие уравнения называются линейными уравнениями с постоянными коэффициентами.
1. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффици-
ентами. Рассмотрим линейное однородное уравнение второго порядка
y |
py |
qy |
0, |
(4.12) |
где р и q действительные числа. |
|
|
||
Теорема 6. 1) Если число |
k |
действительный корень |
||
уравнения |
|
|
|
|
k 2 |
pk |
q |
0, |
(4.13) |
137
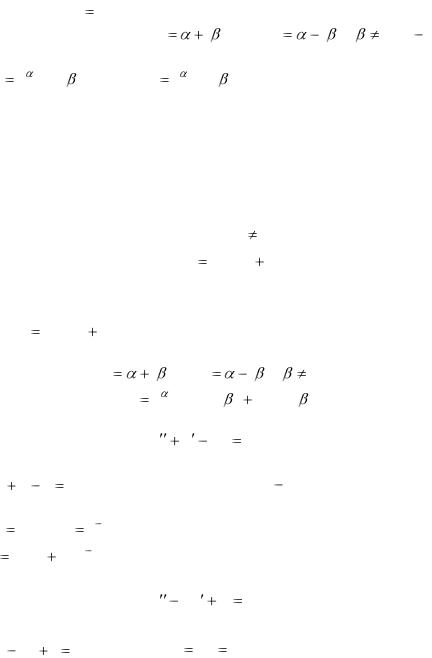
то функция y |
ek x является решением уравнения (4.12). |
||||||||
2) Если |
числа |
|
k1 |
i |
и |
k2 |
i |
( |
0) |
комплексные |
корни |
|
уравнения |
(4.13), то |
|
функции |
|||
y e x cos x |
и |
y |
2 |
e x sin |
x |
являются |
решениями |
||
1 |
|
|
|
|
|
|
|
|
|
уравнения (4.12). |
|
|
|
|
|
|
|
|
|
Уравнение |
(4.13) |
называется |
характеристическим |
||||||
уравнением данного уравнения (4.12). |
|
|
|
|
|||||
Характеристическое |
уравнение |
(4.13) |
|
является |
|||||
квадратным уравнением и, следовательно, имеет два корня. Обозначим их k1 и k2 .
Теорема 7. 1) Если корни характеристического уравне-
ния действительные и различные ( k1 |
k2 ), то общее решение |
|||
уравнения (4.12) имеет вид |
y C ek1x |
C |
2 |
ek2 x ; |
|
1 |
|
|
|
2) если корни характеристического уравнения действительные и равные ( k1 = k2 ), то общее решение имеет вид y C1ek1x C2 xek1x ;
3)если корни характеристического уравнения
комплексные |
|
( k1 |
i , |
k2 |
|
|
i |
, |
0 ), |
то общее |
||||||
решение имеет вид |
y e x (C cos |
x |
|
C |
2 |
sin x). |
|
|
||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
Пример 1. Найти общее решение уравнения |
|
|
|||||||||||||
|
|
|
|
|
|
|
y |
y |
2y |
0 . |
|
|
|
|
||
|
Решение. Характеристическое |
|
уравнение |
имеет |
вид |
|||||||||||
k 2 |
k |
2 |
0 ; |
его корни |
k = 1, |
k |
2 |
= |
2 действительные и |
|||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
различные. |
|
Соответствующие |
частные |
решения |
уравнения |
|||||||||||
y |
e x , |
y |
2 |
|
|
e 2x . |
Общее |
решение |
уравнения |
имеет |
вид |
|||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
C ex |
C |
2 |
e 2x . |
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2. Найти общее решение уравнения |
|
|
|||||||||||||
|
|
|
|
|
|
|
y |
2 y |
y |
0 . |
|
|
|
|
||
|
Решение. |
Характеристическое |
|
уравнение |
имеет |
вид |
||||||||||
k 2 |
2k |
1 |
|
0 ; его корни k |
k |
2 |
1 действительные и равные. |
|||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
138

Соответствующие частные |
|
решения |
|
уравнения |
y |
e x , |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
y2 |
xex . |
|
|
Общее |
|
решение |
уравнения |
имеет |
вид |
||||||||||
y C ex |
C |
2 |
xex |
ex (C C |
2 |
x) . |
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
Пример 3. Найти общее решение уравнения |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
y |
4y |
13y |
0 . |
|
|
|
|
|
||||
|
Решение. |
Характеристическое |
уравнение |
имеет |
вид |
||||||||||||||
k 2 |
4k |
13 |
|
0 ; его корни k |
|
|
2 |
i3, |
k |
2 |
2 i3 комплексные. |
||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
Соответствующие частные решения уравнения |
y |
|
e2x cos3x, |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
y2 |
e2x sin 3x . |
Общее |
решение |
уравнения |
|
имеет |
вид |
||||||||||||
y |
e2x (C cos3x |
C |
2 |
sin 3x) . |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
Линейные |
неоднородные |
|
дифференциальные |
||||||||||||||
уравнения |
|
второго |
|
порядка |
|
|
с |
постоянными |
|||||||||||
коэффициентами. Рассмотрим линейное неоднородное уравнение второго порядка
y py qy |
f (x), |
(4.14) |
где р и q действительные числа; |
f (x) непрерывная функция. |
|
Как известно, общее решение такого уравнения представляет собой сумму частного решения неоднородного уравнения и общего решения соответствующего однородного уравнения. Общее решение однородного уравнения мы находить умеем, поэтому остается рассмотреть вопрос о нахождении частного решения. Для нахождения частного решения можно применять метод вариации произвольных постоянных. Однако если в правой части уравнения (4.14)  многочлен, либо показательная функция, либо тригонометрическая функция sin x или cos x , либо линейная
многочлен, либо показательная функция, либо тригонометрическая функция sin x или cos x , либо линейная
комбинация перечисленных функций, то частное решение может быть найдено методом неопределенных коэффициентов, не содержащим процесса интегрирования.
Рассмотрим различные виды правых частей уравнения
(4.14).
139
