
3447
.pdf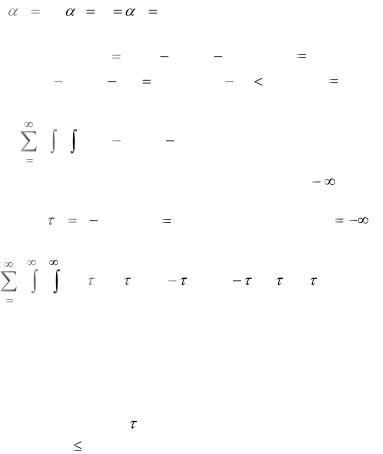
В частном случае, когда в интегро – степенном члене
(6.25) |
0 |
0, |
1 |
... |
n |
1, |
а ядра |
интегралов обладают |
||||
|
|
|
|
|
|
|
|
|
|
|||
свойствами |
|
|
|
|
|
|
|
|
|
|
|
|
1. Kn (t, t1,..., tn ) |
Kn (t |
|
t1,..., t tn ) |
для |
n |
1,2,..., |
||||||
|
2. Kn (t |
t1,..., t tn ) 0, |
если t |
tk |
0 |
для |
k |
1,2,..., n, |
||||
интегро – степенной ряд (6.26) обращается в ряд Вольтерра: |
||||||||||||
|
|
t |
t |
|
|
|
|
|
|
|
|
|
|
|
... Kn (t |
t1,..., t |
tn )u(t1)...u(tn )dt1...dtn , |
(6.27) |
|||||||
|
n 1 |
a |
a |
|
|
|
|
|
|
|
|
|
где нижний предел в интегралах может быть равен |
|
. |
||||||||||
Если во всех интегралах (6.27) выполнить замену |
||||||||||||
переменных |
k |
t tk |
для k |
|
1,2,..., n, , и положить a |
, то |
||||||
ряд Вольтерра примет вид |
|
|
|
|
|
|
|
|||||
|
... |
Kn ( 1,..., n )u(t |
1 )...u(t |
|
n )d 1...d |
n . |
(6.28) |
|||||
|
n 1 0 |
0 |
|
|
|
|
|
|
|
|
|
|
В такой форме ряды Вольтерра чаще всего встречаются в приложениях.
Пусть сумма ряда (7.27) или (7.28) равна v(t) и аргумент t имеет смысл времени. Из вида членов ряда следует, что значение функции v(t) в момент времени t определяется значениями функции u( ) во все предшествующие моменты времени 
 t . Таким образом, если физическая величина v(t) определяется формулой (7.27) или (7.28) через величину u(t) , то физическая система обладает памятью – система
t . Таким образом, если физическая величина v(t) определяется формулой (7.27) или (7.28) через величину u(t) , то физическая система обладает памятью – система
“помнит”' свою историю. Именно это свойства обусловливает применение рядов Вольтерра для описания свойств физических и технических систем. В частности, ряд вида (7.28) используется в механике полимеров для представления связи между напряжением и деформацией.
230
7. ПРИБЛИЖЕННЫЕ АНАЛИТИЧЕСКИЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
7.1. Необходимость асимптотических методов
При построении приближенных решений алгебраических, дифференциальных и интегральных уравнений, а также при оценке различных интегралов приходится иметь дело с рядами по степеням параметра или независимой переменной. В разделе “Функциональные ряды и их приложение” рассматриваются решения некоторых дифференциальных уравнений в виде сходящихся степенных рядов.
Среди причин, затрудняющих поиск точного решения физических и инженерных задач, можно указать нелинейность уравнения, наличие переменных коэффициентов, а также нелинейные граничные условия. Для таких задач часто не удается построить решение в виде сходящегося степенного ряда. Обычно в этих случаях используют комбинацию аналитических и численных методов. Из наиболее используемых и мощных аналитических методов можно отметить метод возмущений (асимптотических разложений) по большим или малым значениям координаты или входящего в уравнение параметра.
К асимптотическим методам обращаются в тех случаях, когда пытаются строить решение дифференциального уравнения в виде степенного ряда в окрестности нерегулярной особой точки. Может оказаться, что полученный ряд является всюду расходящимся. Дело в том, что при этом выпадает краеугольный результат теории – утверждение, что в окрестности регулярной особой точки сходятся все степенные ряды.
Пример. Построить решение в виде степенного ряда для дифференциального уравнения
x3u (x2 x)u u 0 , |
u |
an x n . |
|
n |
0 |
Решение. Вычислим первую и вторую производную
231

|
u |
|
na xn 1, |
u |
|
n(n 1)a |
n |
xn 2 |
|
|
||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
n 1 |
|
|
|
|
|
|
n |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
и подставим в дифференциальное уравнение. Имеем |
|
|
||||||||||||||||||||
|
n(n 1)a |
n |
xn 1 |
|
|
na (xn 1 |
xn ) |
|
|
a |
n |
xn |
|
0 . |
|
|||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|||
n 2 |
|
|
|
|
|
|
|
n 0 |
|
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
Приравнивая нулю коэффициенты при различных |
||||||||||||||||||||||
степенях x , получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x0 : a0 |
0 ; |
|
|
|
|
|
|
x1 : a1 |
|
a1 |
|
|
|
0 ; |
|
|
|
|||||
x2 : a a |
2 |
|
0 ; |
|
|
|
x3 : 4a |
2 |
2a |
3 |
0 ; … ; |
|||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
xn : |
(n 1)an |
|
(n 1)2 an 1 |
0 ,… . |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Отсюда получаем: |
|
a0 |
|
0 , |
a1 – произвольно, |
a2 |
|
|
a1, |
|
||||||||||||
|
a3 |
2a1 , |
|
a4 |
2 3a1 , a5 |
2 3 4a1 , …, |
|
|
|
|||||||||||||
|
|
|
|
|
a |
n |
( |
1)n |
1(n |
1)! a , … . |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, получили формальное решение в виде ряда |
|
|||||||||||||||||||||
|
|
|
|
|
u |
a |
|
n |
1 |
|
x n , |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
( |
1) |
(n |
1)! |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
который |
расходится при всех x , кроме точки |
x |
|
0 . |
|
|
||||||||||||||||
7.2. Калибровочные функции. Символы |
|
порядка |
|
|||||||||||||||||||
Одним из основных элементов асимптотического анализа |
||||||||||||||||||||||
является |
исследование |
пределов |
функций |
|
f ( |
) |
|
|
при |
|
0 , |
|||||||||||
где |
0 . Если предел функции существует, то имеет место |
|||||||||||||||||||||
одна из |
альтернатив: |
при |
|
0 , |
f ( ) |
|
0 ; |
|
f ( |
) |
; |
|||||||||||
f ( ) |
A , где 0 |
A |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Однако для целей анализа такая классификация слишком груба: существует бесчисленное множество функций, обладающих такими пределами. Для уточнения приведенной классификации каждый из трех указанных классов функций
232

подразделяют в соответствии со скоростью, с которой они стремятся к своим пределам. Поэтому сравнивают скорость убывания или возрастания этих функций с соответствующими характеристиками эталонных функций. Эти функции сравнения называются калибровочными функциями.
Наиболее употребительные из калибровочных функций следующие ( 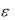 0 ):
0 ):
1. |
Целые |
|
положительные |
|
|
|
|
степени |
параметра |
||||||||||||||||||||
|
: |
|
|
1, |
, |
2,..., |
|
n,... |
0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2. |
Обратные |
|
|
|
|
степени |
|
|
|
|
|
|
этого |
|
|
|
параметра: |
||||||||||||
|
: |
|
|
1 , |
2,..., |
|
|
n,... |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3. |
Показательные |
и |
|
логарифмические |
функции: e |
, |
|||||||||||||||||||||||
|
|
1 |
|
n |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
n , |
|
1 |
|
|
|
|
|
|
|
ln |
|
, |
e e x |
|
0 , |
e , |
|
ln |
e x |
|
. |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Иногда |
|
приходится |
рассматривать |
|
|
и |
|
другие |
|||||||||||||||||||||
калибровочные функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Вместо утверждения о том, что sin |
0 |
c |
той |
же |
|||||||||||||||||||||||||
скоростью, что |
и |
|
|
|
|
0 , говорят |
что « sin |
имеет порядок |
|||||||||||||||||||||
при |
|
|
|
0 » и пишут sin |
O( |
) |
|
при |
0 . |
|
|
|
|
||||||||||||||||
В |
общем |
случае |
полагают |
|
|
f ( |
) |
|
|
O g( |
) при |
|
0 , |
||||||||||||||||
если существует такое число |
A , |
что |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
lim |
f ( |
) |
|
A, |
0 |
|
A |
|
. |
|
|
|
|
(7.1) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
0 g( |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Таким образом, при |
|
|
0 |
|
имеют место соответствия: |
||||||||||||||||||||||||
cos |
O(1) , |
sh |
O( |
) , |
|
ctg |
|
|
O( |
|
|
|
1 ) , sh1 |
O( 1 ) , |
|||||||||||||||
tg O( |
) , |
cos |
1 |
|
O( |
2) , |
|
sch1 |
O(e 1 |
) . |
|
|
|||||||||||||||||
Настоятельно рекомендуем проверить все эти равенства. Введенное с помощью символа « O » математическое
понятие порядка, формально отличается от физического понятия величин, так как по определению (7.1) значение
233

постоянной A может быть сколь угодно большой, но конечной. Однако обычно принимается, что соответствующий коэффициент порядка единицы и значение, определяемое символом порядка достаточно близко к фактическому значению физической величины.
Помимо введенного символа порядка 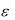 для характеристики скорости изменения функции относительно калибровочной функции вводится еще один символ o(g( )) определяемый следующим образом
для характеристики скорости изменения функции относительно калибровочной функции вводится еще один символ o(g( )) определяемый следующим образом
|
|
f ( ) |
|
o(g( |
)) |
при |
0 , |
|
если |
|
lim |
|
f ( |
) |
|
0 . |
(7.2) |
||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 g( |
) |
|
|
|
||
|
|
Рекомендуется проверить следующие соответствия |
при |
||||||||||||||||||||||||||
|
|
0 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
o(1) , |
|
cos |
o( |
1 ) , |
|
|
sin |
|
o( |
1 2) , |
|
cos |
o( |
1 2) , |
||||||||||||||
e |
1 x |
|
o(e |
e x |
) , |
ln1 |
|
|
o( |
0.001 |
, |
ln ln1 |
|
|
o(ln1 |
) . |
|||||||||||||
|
|
|
|
|
|
|
|
) |
|
|
|||||||||||||||||||
|
|
|
7.3. |
|
|
Пример асимптотического разложения. |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
Определение асимптотического ряда |
|
|||||||||||||||||||||
|
|
Сделаем оценку интеграла при больших |
|
|
0 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
f ( ) |
|
|
|
|
|
e x dx. |
|
|
|
|
|
(7.3) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разложим в степенной ряд множитель при экспоненте в |
|||||||||||||||||||||||||||
подынтегральной функции. Получаем |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
x |
|
x 2 |
... |
|
( |
1)n |
x |
n |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(7.4) |
||||||
|
|
|
x |
1 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
0 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Полученный ряд (геометрическая прогрессия) сходится при x 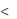 . Подставим разложение (7.4) в (7.3), найдем
. Подставим разложение (7.4) в (7.3), найдем
234
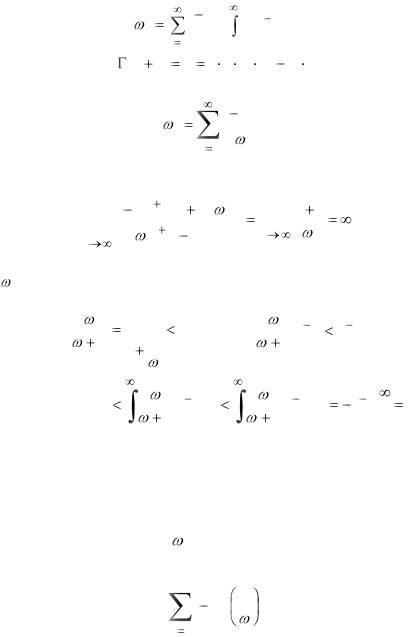
|
|
|
|
f ( |
) |
|
|
|
|
|
( |
1)n |
|
|
|
xne x dx, |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
n |
0 |
|
n |
0 |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
(n |
1) |
|
n! |
1 2 ... (n |
|
|
1) |
n, |
|
|
|
|
||||||||||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
f ( |
) |
|
|
|
( |
1)n n! |
. |
|
|
|
|
|
|
|
(7.5) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для выяснения вопроса о сходимости ряда применим |
|||||||||||||||||||||||||||||||||||
признак Даламбера к ряду (7.5), получим |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
( 1)n |
|
1(n |
1)! |
|
|
n |
|
|
|
lim |
|
n |
1 |
. |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
lim |
|
|
|
|
|
n |
1( |
|
1)n n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Следовательно, ряд (7.5) расходится при всех значениях |
|||||||||||||||||||||||||||||||||||
. Получается так, |
|
что равенство (7.5) |
не имеет смысла. |
С |
|||||||||||||||||||||||||||||||
другой стороны, поскольку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
1 |
|
|
|
1, |
|
|
|
|
то |
|
|
|
|
|
e |
x |
e x . |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Далее имеем 0 |
|
|
|
|
|
|
|
|
e |
|
x dx |
|
|
|
|
|
|
|
|
|
e x dx |
e x |
0 |
1. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Следовательно, интеграл сходится. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Следует заметить, что расходимость ряда (7.5) связана с |
|||||||||||||||||||||||||||||||||||
незаконностью почленного интегрирования ряда (7.4) |
|
вне |
|||||||||||||||||||||||||||||||||
интервала его сходимости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Однако формулу (7.5) все же можно использовать для |
|||||||||||||||||||||||||||||||||||
вычисления функции |
|
|
f ( |
|
) после некоторой модификации. |
|
|||||||||||||||||||||||||||||
Ограничимся в ряде (7.4) конечным числом членов |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
1)n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
n |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
235
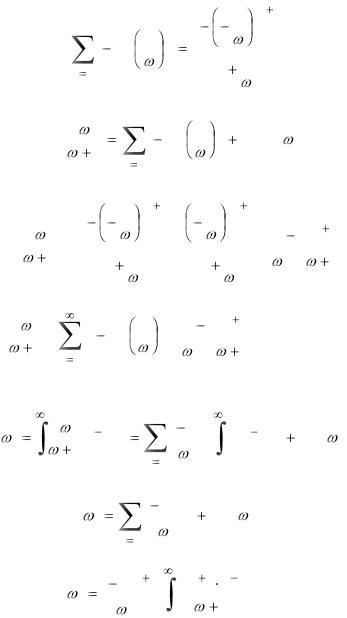
и найдем сумму, заметив, что отрезок ряда является геометрической прогрессией
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
x N |
1 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
1)n |
|
|
|
x |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
x |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
n |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Следовательно, |
|
можно |
|
записать |
|
|
в |
соответствии с |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
x |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
формулой (7.4) |
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
1)n |
|
|
|
|
|
RN (x, |
) , |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где RN – остаток ряда определяется формулой |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
x |
|
|
N |
1 |
|
|
|
|
|
|
|
x |
|
|
N |
1 |
|
|
|
|
|
|
|
|||||||||||||
RN = |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
( |
x) N |
1 |
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
N ( |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
x) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Таким образом, формулу (7.4) запишем теперь в виде |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
= |
|
|
|
|
|
( |
|
1)n |
|
|
x |
n + |
|
( |
x) N |
1 |
|
. |
|
|
|
(7.6) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N ( |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
x |
n |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x) |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Подставим, как и ранее в подынтегральное выражение |
||||||||||||||||||||||||||||||||||||||||||||||||
(7.3), получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
f ( ) |
|
|
|
|
|
|
e x dx |
|
|
|
|
N ( |
1)n |
|
|
|
|
xne x dx RN ( ), |
||||||||||||||||||||||||||||||
|
|
|
x |
|
|
|
|
n |
0 |
|
|
|
n |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
f ( |
) |
|
|
|
N |
( |
|
|
1)n n! |
|
RN ( |
) , |
|
|
|
(7.7) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где остаток |
|
|
|
|
|
|
|
|
n |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
( 1) N 1 |
|
|
x N |
1 |
|
e |
x |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
RN ( |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx . |
|
|
|
(7.8) |
||||||||||
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
236

|
Для сходимости ряда необходимо, |
чтобы |
RN |
0 |
при |
|||||||
N |
. Но в |
нашем |
случае RN |
при |
N |
|
|
|
|
в |
||
соответствии с признаком |
Даламбера. |
|
|
|
|
|
|
|
|
|||
|
Принципиальный момент заключается в том, что мы |
|||||||||||
зафиксируем номер |
N и оценим величину остатка |
RN ( |
) |
|||||||||
при |
0 . Так |
как |
и |
0 и x |
0 , |
то |
1 |
|
|
|
1 |
, |
|
x |
|
x |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
поэтому из (7.8) получаем |
|
|
|
|
|
|
|
|
|
|||
|
RN ( ) |
|
1 |
|
x N 1 |
e |
x dx |
1 |
x N e |
x dx |
N! |
. |
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||
|
|
|
|
N |
0 |
x |
|
N |
0 |
|
N |
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Итак, ошибка, вызванная усечением ряда (7.5) на N - ом |
||||||||||||
члене, не |
превосходит первого отброшенного члена – ( N 1)- |
||||||||||||
го члена. |
К тому же при фиксированном N и |
|
имеем |
||||||||||
RN ( ) |
0 . |
|
|
|
|
|
|
|
|
|
|
||
|
Поэтому, хотя ряд (7.5) и расходится, но для |
||||||||||||
фиксированного N первые N членов ряда приближают |
|||||||||||||
функцию |
f ( |
) c |
ошибкой, |
которую |
можно |
сделать сколь |
|||||||
угодно малой выбором достаточно большого значения .
|
Такой ряд называется |
асимптотическим |
рядом типа |
|||||||||||
Пуанкаре и обозначается f ( |
) |
( |
1) |
n |
|
n! |
. |
|
||||||
|
|
n |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
0 |
|
|
|
|
|
|
|
|
Определение. |
Ряд вида |
|
an |
|
, |
|
где an |
не зависит |
|||||
|
|
n |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
от |
, |
называется |
асимптотическим |
|
|
рядом |
и пишут |
|||||||
f ( |
) |
|
an |
при |
тогда |
и |
|
только тогда, когда |
||||||
|
n |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
237

|
N |
|
an |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
f ( ) |
|
|
o |
|
|
|
|
при |
. |
|
(7.9) |
||||||||
|
|
|
|
n |
|
|
N |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Поскольку |
N |
|
an |
|
o( |
|
N |
) |
N 1 an |
|
aN |
o( |
N |
) , |
|||||
|
|
|
|
n |
|
|
|
|
n |
|
N |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
n |
0 |
|
|
|
|
|
|
|
|
n 0 |
|
|
|
|
|
||
то условие (7.9) можно записать в виде
|
N |
an |
|
|
|
|
|
|
f ( ) |
|
o( |
N |
) |
при |
. |
(7.10) |
|
|
n |
|
||||||
|
|
|
|
|
|
|
|
n0
Взаключении отметим, что полезность асимптотических
рядов основана на том, что ошибка, получаемая при усечении ряда быстро стремится к нулю при 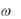 . В вычислениях обычно фиксируют достаточно большое значение параметра
. В вычислениях обычно фиксируют достаточно большое значение параметра 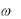 и пытаются уменьшить ошибку увеличением числа членов асимптотического ряда. Поскольку ряд расходится, то достигается такое N, за которым добавление новых членов лишь увеличивает ошибку, ведь
и пытаются уменьшить ошибку увеличением числа членов асимптотического ряда. Поскольку ряд расходится, то достигается такое N, за которым добавление новых членов лишь увеличивает ошибку, ведь 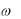 - конечно. Таким образом, для заданного , существует оптимальное значение N, при котором ошибка минимальна. Практически такое значение N можно отследить, используя ПЭВМ.
- конечно. Таким образом, для заданного , существует оптимальное значение N, при котором ошибка минимальна. Практически такое значение N можно отследить, используя ПЭВМ.
Для справки приведем практически используемый асимптотический ряд для одной из функций Бесселя
|
|
|
|
|
J0 (x) |
1 |
x2 |
|
x4 |
|
|
x6 |
|
, |
|
|
|||
|
|
|
|
|
22 |
22 |
42 |
|
22 |
42 |
62 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
причем ряд |
сходится |
абсолютно и |
равномерно при |
|
всех |
||||||||||||||
значениях х. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J0 (x) |
2 |
|
|
u(x) cos |
x |
|
|
|
v(x) sin |
x |
|
|
|
при |
x |
, |
|||
|
|
|
|
|
|
|
|
|
|||||||||||
x |
4 |
|
4 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где
238
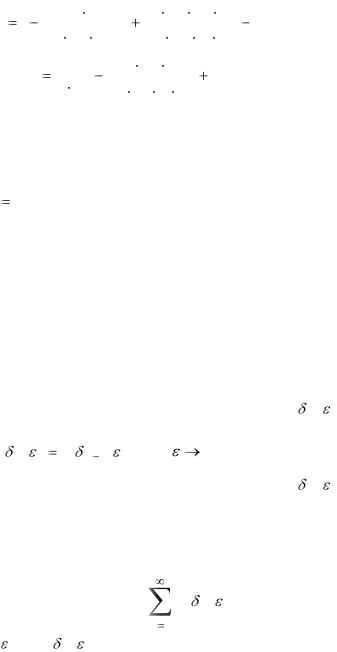
u(x) 1 |
|
|
12 |
32 |
|
|
12 |
32 |
52 |
72 |
, |
|||
|
42 22 2!x 2 |
|
|
42 22 4! x 4 |
||||||||||
v(x) |
1 |
|
|
12 |
32 |
52 |
|
. |
||||||
4 2x |
43 23 3! x3 |
|||||||||||||
Ряды для u(x) |
и v(x) |
расходятся при всех значениях х. |
||||||||||||
Для малых |
х первые несколько членов ряда J 0 (x) дают |
|||||||||||||
хорошую точность. Например, J 0 (2) дают верные 11 значений цифр, если ограничиться девятью членами разложения.
При x 4 восемь членов ряда J 0 (2) дают точность до
3-й значащей цифры, в то время как такую же точность обеспечивает уже первый член асимптотического разложения.
7.4. Асимптотические последовательности и асимптотические разложения
Ранее для оценки скорости изменения функций были введены калибровочные функции. Вместе с тем для асимптотического представления заданной функции не обязательно ограничиваться перечисленными функциями сравнения. Вместо них можно использовать произвольную
последовательность |
функций |
общего |
вида |
n ( |
) , |
|
удовлетворяющих условию |
|
|
|
|
|
|
n ( ) |
o( n 1( )) при |
0 . |
|
(7.11) |
||
Определение. |
Последовательность |
функций |
n ( |
) , |
||
удовлетворяющих условию (7.11) называется асимптотической последовательностью. Через асимптотическую последовательность можно определить и асимптотическое разложение.
Определение. |
Сумма |
вида |
an n ( ) , где an не |
|
|
n |
0 |
зависит от , а |
n ( ) |
представляет собой асимптоти- |
|
239
