
3447
.pdf
y (q(x) p(x))y (v 1).
(q(x) p(x))y (v 1).
Уравнение (2.58) также будет являться уравнением с
разделяющимися переменными |
при p(x) |
q(x) . |
Ниже мы |
|||||||||||
рассмотрим случай, когда v |
0 , |
v |
1. Относительно функций |
|||||||||||
p(x) и q(x) будем предполагать, |
что они непрерывны при |
|||||||||||||
|
|
q(x) |
|
|
|
|
|
|
|
|
|
|
||
x (a,b) и |
p(x) |
|
. |
|
|
|
|
|
|
|
|
|||
1. Уравнение Бернулли сводится к линейному уравнению |
||||||||||||||
подстановкой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y1 v ) . |
|
|
||
|
|
|
y |
z1 |
v , |
(z |
|
|
(2.59) |
|||||
Действительно, применив эту подстановку, найдем |
||||||||||||||
производную новой функции |
|
|
|
|
|
|
||||||||
|
|
|
|
|
z |
|
(1 v) y |
v y . |
|
|
|
|||
Умножив |
обе |
части |
уравнения |
(2.58) на |
(1 v) y v |
|||||||||
(предполагая, |
что |
|
|
|
y |
0 |
если |
v |
0 ), |
получим |
||||
дифференциальное уравнение для новой функции |
|
|||||||||||||
|
|
z (1 v) p(x)z |
(1 |
v)q(x), |
|
(2.60) |
||||||||
которое является линейным уравнением. Интегрируя полученное уравнение методом, изложенным в п.2.4, получим общее решение уравнение Бернулли в виде
1
y 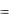 e(v 1)
e(v 1) p(x)dx C (1 v)
p(x)dx C (1 v)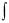 q(x)e(1 v)
q(x)e(1 v) p(x)dx dx
p(x)dx dx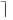 1 v . (2.61)
1 v . (2.61)
Читателю рекомендуется самостоятельно получить это решение. Таким образом, уравнение Бернулли также
интегрируется в квадратурах. |
|
|
|
|
|
|
2. Помимо общего решения уравнение |
Бернулли |
при |
||
v |
0 имеет еще очевидное решение y |
0 (при v |
0 функция |
||
y |
0 не является решением уравнения). При 0 |
v |
1 решение |
||
y |
0 не содержится в формуле |
общего |
решения. |
Оно |
|
является особым решением, поскольку в каждой точке этого решения нарушается единственность решения задачи Коши.
50
При v 1 решение y |
0 является частным решением, так |
||
как в этом случае |
через точки оси OX не проходит ни одна |
||
интегральная |
кривая (кроме y 0 , т.е. самой оси OX ) . Таким |
||
образом, при |
v |
1 во |
всякой точке оси OX решение |
существует |
и единственно. Формально это |
решение можно |
|
включить в семейство (2.61), положив C |
. |
|
|
3. При решении уравнения Бернулли нет необходимости пользоваться готовой формулой (2.61). Проще превратить его в линейное уравнение, используя подстановку (2.59), или же непосредственно использовать метод Бернулли, отыскивая
решение уравнения в виде y |
|
|
u |
v . |
|
|
|
|
|
|
|
|
||
Пример. Найти решение уравнения xy |
y |
y2 ln x. |
||||||||||||
Решение. Разделив обе части уравнения на |
x видим, что |
|||||||||||||
это уравнение типа (2.50) при v |
2 . Разыскиваем его решение |
|||||||||||||
в виде произведения двух функций |
|
y u |
v . |
Подставим в |
||||||||||
уравнение y u v uv , y |
u v , получим: |
|
|
|
|
|||||||||
u v |
uv |
1 |
|
uv |
u |
2 |
v |
2 ln x |
, |
|
|
|||
x |
|
|
x |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
u v |
u v |
|
|
v |
|
u |
2 |
v |
2 ln x |
|
. |
|
|
|
|
|
x |
|
|
|
x |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Накладываем условие равенства нулю второго слагаемого в левой части уравнения. Получаем совокупность связанных дифференциальных уравнений:
u v |
v |
0, |
|
|
|||
x |
|||
|
(*) |
||
|
|
u v u 2v2 lnxx .
Решаем первое уравнение. Имеем:
u |
0, |
|
|
y 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
dv |
|
v |
, |
|
dv |
|
dx |
, |
ln |
|
v |
|
ln |
|
x |
|
1, v |
1 |
, |
|
|
|
|
|
|
||||||||||||||
dx |
|
x |
|
v |
x |
x |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
51

где |
|
|
в качестве |
решения |
уравнения |
с |
|
разделяющимися |
||||||||||||||||||||||||||||||
переменными взяли частное решение при |
C |
0 |
|
(см. п.2.4). |
||||||||||||||||||||||||||||||||||
Подставляя во второе уравнение совокупности |
(*) |
|
v |
1 x , |
||||||||||||||||||||||||||||||||||
получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 du |
u 2 ln x |
, |
|
|
du |
|
|
|
|
ln x |
dx, |
|
1 |
|
|
|
ln x |
dx. |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
x dx |
x2 |
x |
|
|
u 2 |
|
|
|
|
x2 |
|
|
u |
|
|
|
x2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Интеграл в правой части равенства вычисляем методом |
||||||||||||||||||||||||||||||||||||
интегрирования по частям UdV |
UV |
VdU. Имеем: |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
U |
ln x, |
dU |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln x |
|
dx |
|
|
ln x |
|
1 |
|
|
|||||||||||||
x |
2 |
ln xdx |
|
|
|
x |
|
|
|
|
|
|
|
C. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
dV x |
2 dx, V |
|
|
|
1 |
|
|
|
x |
|
x 2 |
|
|
|
x |
|
x |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Таким образом, имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
1 |
|
|
ln x |
1 |
|
C, |
|
|
|
|
u |
|
|
|
|
x |
|
. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
u |
|
|
x |
|
|
|
|
|
|
|
|
|
ln x |
|
1 |
|
Cx |
|
|
|
|
|||||||||
Общее решение уравнения имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
1 |
|
|
|
|
, |
|
|
C ( |
|
, ). |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ln x 1 Cx |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
К нему следует присовокупить частное решение |
|
y |
0 , |
|||||||||||||||||||||||||||||||||
которое формально можно получить из общего решения при
C |
. |
|
4. Рассмотрим задачу о построении линии по ее |
геометрическим свойствам, сводящуюся к дифференциальному уравнению Бернулли.
Найти линии, у которых отрезок, отсекаемый касательной
на оси OY , равен квадрату ординаты точки касания. |
|
|
|||||||
По условию задачи (см. |
рис. |
7) |
OA |
BM 2 . |
Обозначим |
||||
координаты точки |
M через |
x, y , где |
M - произвольная точка |
||||||
искомой линии. |
Тогда BM |
y . |
Отрезок OB |
найдем |
из |
||||
уравнения |
касательной |
Y |
y |
y (X |
x) , где X ,Y |
- |
|||
координаты текущей точки касательной с угловым коэффициентом, равным y . Положив в уравнении касательной
52

X 0, |
найдем |
OA |
Y y |
|
xy . |
Таким |
образом, |
|||
дифференциальное уравнение задачи имеет вид: |
|
|||||||||
|
|
y2 |
|
y |
|
y |
|
y 2 |
|
|
|
y xy |
или |
|
|
|
|
. |
|
||
|
|
|
|
|
||||||
|
|
|
|
|
|
x |
|
x |
|
|
y A
|
M |
|
1 |
|
y 1 |
0 |
B |
x |
,
Рис.7 Полоса единственности решения линейного уравнения
Найдем решение полученного уравнения Бернулли, используя метод сведения к линейному уравнению. Используя
подстановку (2.61) для |
v 2 . |
Полагая y |
1 |
|
z, z |
y |
2 y , |
||||||||||||||
получим линейное уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
z |
|
z |
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Воспользуемся формулой (2.52), выражающей общее |
||||||||||||||||||||
решение |
линейного уравнения. |
В |
нашем |
случае |
p(x) |
|
1 |
, |
|||||||||||||
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
q(x) |
|
1 |
|
. Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
p(x)dx |
ln x , |
|
|
exp |
p(x)dx |
1 |
; |
|
|
|
|
||||||
|
|
|
|
|
|
|
x |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q(x) exp |
p(x)dx dx |
|
1 |
xdx |
|
x |
C. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
53 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
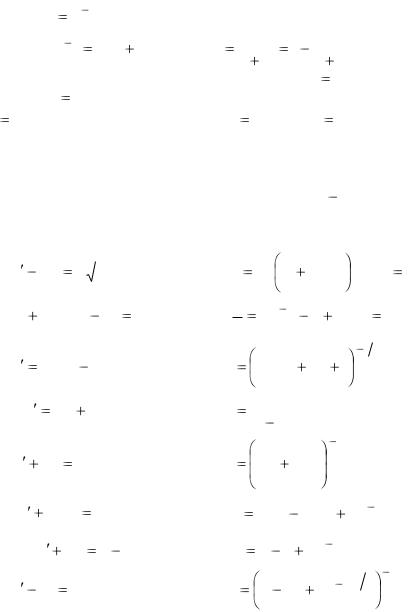
Заменяя z |
y 1 , получим: |
|
|
|
|
|
|
|
|
|
|||||
|
y |
1 |
1 |
(x |
C), |
или y |
|
x |
|
1 |
|
|
C |
. |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
x |
|
|
|
x |
C |
|
x |
C |
|
|||
Искомые линии – гиперболы. При |
C |
0 |
|
получаем |
|||||||||||
прямую |
y |
1. Кроме того, решением является также прямая |
|||||||||||||
y 0 . |
Очевидно, |
что |
прямые |
y 0 |
|
и |
|
y |
1 |
|
обладают |
||||
требуемым свойством (это видно и без построения дифференциального уравнения). Отметим, наконец, что полученное уравнение Бернулли можно было решить с помощью разделения переменных, так как p(x) 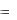 q(x) .
q(x) .
Задачи для самостоятельного решения
1. y |
4 y |
|
|
|
|
x y. |
|||||
|
|||||
x |
|||||
|
|
|
|
||
2. ( y xy2 )dx dy 0.
3. |
y |
x3 y3 |
xy . |
|||
4. |
x2 y |
|
|
y2 |
xy. |
|
5. |
xy |
2y |
x5 y2. |
|||
6. |
yy |
|
1 |
y2 |
sin x. |
|
2 |
||||||
|
|
|
|
|||
7. |
3y2 y |
y3 x 1. |
||||
8. |
y |
xy |
x3 y2. |
|||
Ответ: y
Ответ: 1y
Ответ: y
Ответ: y
Ответ: y
Ответ: y2
Ответ: y3
Ответ: y
x4 |
|
|
1 |
|
|
2 |
|
|||
C |
|
ln x |
, |
y 0. |
||||||
2 |
||||||||||
|
|
|
|
|
|
|
|
|||
|
Ce |
x |
|
x |
1, |
y |
0. |
|||
Ce x 2 |
|
x2 |
|
1 2 |
||||||
|
1 |
. |
||||||||
|
x |
|
. |
|
|
|
||||
|
|
|
|
|
|
|||||
C ln x |
|
|
|
|||||||
|
x5 |
|
|
|
|
|
1 |
|
|
|
|
Cx 2 . |
|
||||||||
3 |
|
|
||||||||
|
|
|
|
|
|
|
|
|||
sin x |
cos x |
|
Ce |
x . |
||||||
|
x |
2 |
Ce |
x . |
|
|||||
|
|
|
x2 |
|
|
|
|
x 2 2 |
1 |
|
2 |
|
|
Ce |
. |
||||||
54
2.6. Уравнение в полных дифференциалах
Мы познакомились в предыдущих параграфах с некоторыми видами дифференциальных уравнений 1-го порядка, допускающих интегрирование в квадратурах. Ниже рассматривается новый тип уравнений, занимающий особое место в теории дифференциальных уравнений. Важность этого типа уравнений связана с тем, что к нему сводятся не только некоторые из ранее изученных уравнений, но и многие другие уравнения. Особенно важна связь таких уравнений с теорией потенциала, без которой невозможно построить термодинамику, электродинамику, гидродинамику и ряд других физических и прикладных дисциплин.
1. Уравнением в полных дифференциалах называется уравнение вида
P(x, y)dx Q(x, y)dy 0, |
(2.62) |
левая часть которого представляет собой полный дифференциал функции U(x, y) , т.е.
P(x, y)dx Q(x, y)dy dU(x, y). |
(2.63) |
Относительно функций P(x, y) и Q(x, y) |
предполагается, |
что они непрерывны по обеим переменным в некоторой односвязной области плоскости (т.е. области без “дырок”) и ни в одной точке этой области не обращаются одновременно в нуль.
Поскольку полный дифференциал функции двух переменных записывается через частные производные
dU |
U |
dx |
U |
dy , |
(2.64) |
|
|
||||
|
x |
y |
|
||
то уравнение в полных дифференциалах (2.62), (2.63) можно переписать в виде
U (x, y) |
dx |
U (x, y) |
dy 0. |
(2.65) |
|
|
|||
x |
y |
|
||
Таким образом, решение этого уравнения сводится к нахождению функции U(x, y) по ее полному дифференциалу. Уравнение (2.65) можно, очевидно, записать так:
55
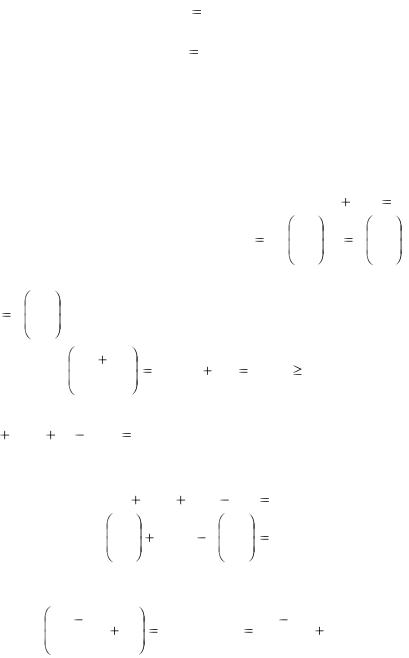
dU(x, y) 0. |
(2.66) |
Поэтому его общий интеграл имеет вид |
|
U(x, y) C. |
(2.67) |
Очевидно, что особых решений уравнение в полных дифференциалах не имеет.
В простейших случаях, когда заранее известно, что левая часть уравнения вида (2.62) представляет собой полный дифференциал, можно воспользоваться методом подведения
под дифференциал. |
|
|
|
|
|
|
|
|
|
Суть этого метода проиллюстрируем на примерах. |
|
|
|
||||||
Пример. Найти общий интеграл уравнения xdx |
ydy |
0. |
|||||||
|
|
d |
|
x2 |
|
x2 |
|
||
Решение. Легко видеть, что |
xdx |
|
|
|
dx |
d |
|
. |
|
dx |
2 |
2 |
|||||||
|
|
|
|
|
|||||
Аналогичное выражение имеем для второго слагаемого:
ydy |
d |
y |
2 |
. Отсюда получаем: |
|
|||
|
|
|
||||||
2 |
|
|||||||
|
|
|
|
|
|
|
||
|
|
|
|
d |
x2 y 2 |
0, x 2 y 2 |
C (C 0). |
|
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
Пример. |
Найти |
общий |
интеграл уравнения |
||||
(x2 |
y)dx (x y)dy 0. |
|
|
|||||
Решение. Сгруппируем члены, входящие в уравнение так, чтобы каждая группа являлась полным дифференциалом:
|
|
x2dx ( ydx |
xdy) |
ydy |
0, |
|
|
|||||
|
|
d |
x2 |
d (xy) d |
y 2 |
0. |
|
|
||||
|
|
2 |
|
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
Отсюда, |
заменяя |
|
сумму |
|
дифференциалов |
на |
||||||
дифференциал суммы, имеем: |
|
|
|
|
|
|||||||
|
x2 |
y 2 |
|
|
|
|
|
|
x2 y 2 |
|
||
d |
|
|
|
xy |
0, |
U (x, y) |
|
xy. |
|
|||
|
2 |
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
56

Следовательно, данное уравнение является уравнением в полных дифференциалах и выражение
(x y)2 2y2 C
есть его общий интеграл.
Приведенные примеры показывают недостатки метода: даже когда известно, что уравнение является уравнением в полных дифференциалах, подобрать соответствующие группы, которые являются полными дифференциалами, не всегда просто. Тем более, что до сих пор мы не привели критерия, по которому можно распознать этот тип уравнения.
Поэтому возникают вопросы: как узнать по виду уравнения в форме (2.62), является ли оно уравнением в полных дифференциалах? В случае если уравнение является таковым, как построить функцию U(x, y) и, следовательно,
общий интеграл этого уравнения?
2. Признак уравнения в полных дифференциалах и построение общего интеграла.
Теорема. Пусть функции P(x, y) и Q(x, y) непрерывны и
имеют непрерывные частные производные |
P |
и |
Q |
внутри |
|
y |
x |
||||
|
|
|
некоторой области a x b , c y d . Тогда необходимым и достаточным условием того, чтобы дифференциальное выражение P(x, y)dx Q(x, y)dy было полным дифференциалом, является равенство частных производных
P(x, y) |
|
Q(x, y) |
. |
(2.68) |
|
|
|
||
y |
|
x |
|
|
Доказательство*. Докажем необходимость условия (2.68). Пусть дифференциальное выражение является полным дифференциалом, то есть справедливо равенство
dU(x, y) P(x, y)dx Q(x, y)dy.
Но тогда отсюда и формулы (2.64) следует, что
P(x, y) |
U |
, |
Q(x, y) |
U |
. |
(2.69) |
|
|
|||||
|
x |
|
|
y |
|
|
57
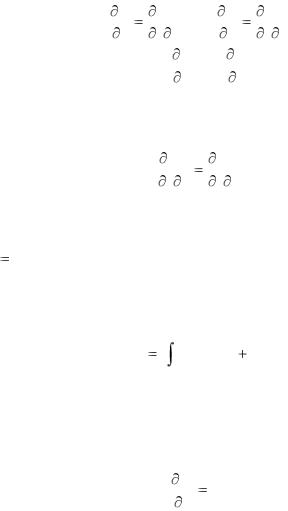
Дифференцируя первое из равенств (2.69) по y , а второе по x , получим:
|
P |
|
2U |
, |
|
Q |
2U |
. |
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
y |
|
x y |
|
|
|
x |
y x |
||||
По предположению |
|
P |
и |
|
Q |
непрерывны, а значит |
||||||
|
|
|
|
|
|
|||||||
|
y |
|
x |
|||||||||
|
|
|
|
|
|
|
|
|
||||
будут непрерывны и смешанные производные. По теореме матанализа о смешанных производных они должны быть равны
2U |
|
2U |
, |
x y |
|
y x |
|
|
|
что влечет равенство (2.68).
Докажем, достаточность условия. Пусть условие (2.68) выполнено. Докажем, что можно построить такую функцию U U (x, y) , полный дифференциал которой удовлетворяет
равенству (2.63). Если такая функция существует, то из (2.63) и (2.64) вытекают равенства (2.69).
Из первого равенства в формулах (2.69) следует, что
|
|
x |
|
|
|
|
|
|
|
|
U (x, y) |
P(x, y)dx |
C( y) . |
|
(2.70) |
||||
|
|
x0 |
|
|
|
|
|
|
|
|
Здесь C(y) - |
произвольная дифференцируемая функция |
|||||||
от y , поскольку при интегрировании по x , |
y рассматривается |
||||||||
как |
постоянная |
величина. |
При |
любом |
выборе |
||||
дифференцируемой |
функции |
C( y) |
и |
нижнего |
предела |
||||
интеграла x0 справедливо |
|
U |
P(x, y). |
|
|
||||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
x
Таким образом, функция (2.70) удовлетворяет первому из условий (2.69).
Покажем, что функцию C(y) можно выбрать так, чтобы
удовлетворялось и второе равенство в (2.69), то есть выполнялось
58

|
|
|
U |
|
|
x |
|
|
|
|
|||
|
|
|
|
|
P(x, y)dx C( y) |
Q(x, y). |
(2.71) |
||||||
|
|
|
|
|
|
|
|||||||
|
|
|
y |
y |
|
||||||||
|
|
|
|
x0 |
|
|
|
|
|||||
|
Вычислим производную и учтем, что по нашему |
||||||||||||
предположению справедливо равенство (2.68). Имеем: |
|
||||||||||||
x |
P(x, y) |
|
|
|
|
x |
Q(x, y) |
|
|
|
|
|
|
|
dx C ( y) |
|
|
dx C ( y) |
Q(x, y) Q(x0 , y) C ( y). |
||||||||
|
|
|
|
|
|||||||||
x0 |
y |
x0 |
x |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||
|
Сравнивая последнее равенство с (2.71), видим: для того, |
||||||||||||
чтобы выполнялось |
требование |
U |
Q(x, y) , надо, |
чтобы |
|||||||||
|
|
||||||||||||
y |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
функция C(y) удовлетворяла дифференциальному уравнению
|
|
dC( y) |
Q(x0 , y) . |
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
||
|
|
|
|
|
||
Отсюда получаем: |
|
|
|
|
|
|
|
y |
|
|
|
||
C( y) |
Q(x0 , y)dy |
(c y0 |
d ) , |
(2.72) |
||
|
y0 |
|
|
|
||
где выбрано решение уравнения, которое при |
y y0 |
|||||
обращается в нуль. Подставляя (2.72) в (2.70), получаем: |
||||||
|
x |
y |
|
|
||
U (x, y) |
P(x, y)dx |
Q(x0 , y)dy. |
(2.73) |
|||
|
x0 |
y0 |
|
|
||
Таким образом доказано, что при выполнении условия |
||||||
(2.68) дифференциальное выражение |
Pdx Qdy |
является |
||||
полным дифференциалом и найдена функция U(x, y) |
полный |
|||||
дифференциал которой равен этому выражению. |
|
|
Из (2.67) получаем, |
что общий интеграл |
уравнения в |
полных дифференциалах имеет вид: |
|
|
x |
y |
|
P(x, y)dx |
Q(x0 , y)dy C. |
(2.74) |
x0 |
y0 |
|
59
