3447

Предел последовательности частичных сумм

называют суммой ряда (6.1). Если функциональный ряд

Если функции uk (x) определены в некоторой области

действительной оси Д, функциональные ряды (6.1) называются сходящимися в области Д, если он сходится в каждой точке этой области.

Определение. Функциональные ряды (6.1) называются абсолютно сходящимися в точке x (в области Д), если сходится в этой точке (в каждой точке области Д) ряд, составленный из абсолютных величин членов ряда (6.1.), т.е.

сходится uk (x) .

k 1

Область абсолютной сходимости ряда (6.1) можно найти используя признаки Даламбера или Коши. Действительно, определяя предел (если он существует)

210

Решение. Используя признак Коши, получим

общий член ряда не стремится к нулю при n . Поэтому эти значения x не входят в область сходимости.

Определение. Функциональный ряд (6.1) называется равномерно сходящимся к своей сумме S(x) на сегменте [a,b] ,

если последовательность частичных сумм (Sn (x))1 сходится равномерно на [a,b] к его сумме S(x) , т.е., если для всякого

для каждого n N( ) сразу при всех x из [a,b] .

Если функциональный ряд (6.1) сходится в области Д, то его сумма будет некоторой функцией f (x) . Возникает

естественный вопрос о связи свойств членов ряда со свойствами его суммы. Оказывается, что если все члены функционального ряда являются непрерывными функциями в области Д, то сумма может быть разрывной функцией.

Имеем:

211

6.2. Свойства равномерно сходящихся рядов. Признак равномерной сходимости

В отличии от рядов, сходящихся поточечно, равномерно сходящиеся ряды обладают свойством коммутативности

Таким образом, коллективное свойство членов ряда – равномерная сходимость, приводит к качественно новым свойствам его суммы.

Наиболее важными свойствами равномерно сходящихся рядов являются следующие.

1.Сумма конечного числа равномерно сходящихся рядов является равномерно сходящимся рядом.

2.Умножение всех членов равномерно сходящегося ряда

на одну и ту же ограниченную функцию (x) (в частности, на

постоянную) не нарушает равномерной сходимости.

3. Если все члены функционального ряда непрерывны на [a, b] и ряд сходится равномерно на [a, b] , то его сумма также

непрерывна на [a,b] .

4. Если функциональный ряд, члены которого непрерывны на [a, b] сходится равномерно на этом отрезке и

S(x) - его сумма, то имеет место равенство

212

ряда S(x) дифференцируема на [a, b] и справедливо равенство

Для установления на практике равномерной сходимости конкретных рядов затруднительно использовать определение равномерной сходимости. С этой целью пользуются более удобными в применении достаточными признаками.

Мажорантный признак Вейерштрасса.

Если члены функционального ряда (6.1) удовлетворяют на [a,b] неравенствам un (x) an , (n 1,2,...) , где an - члены

сходящегося числового ряда, (называемого мажорирующим рядом), то ряд (6.1) сходится равномерно на [a, b] .

сходится равномерно на всей оси, так как для него существует

дифференцировать почленно и найти сумму ряда S1 (x) ,

составленного из производных исходного ряда.

Решение. Вычислим производную общего члена ряда:

213

6.3. Степенные ряды. Интервал сходимости, радиус сходимости

Степенным рядом называется функциональный ряд вида

Поэтому в дальнейшем ограничимся рассмотрением рядов вида (6.5).

В отличии от области сходимости произвольного функционального ряда, которая может оказаться множеством сколь угодно сложной структуры, область сходимости ряда (6.5) всегда является отрезком оси ox , который может быть сегментом, полусегментом или интервалом, может вырождаться в одну точку x 0 или совпадать со всей осью ox . Очевидно, что всякий степенной ряд вида (6.5) сходится при x 0 .Существуют степенные ряды, сходящиеся только в точке x 0 .

214

сходится при всех x , т.е. его область сходимости – вся ось. Этот факт легко проверить, применяя признак Даламбера, как в предыдущем примере. Характер сходимости степенного ряда описывается следующей основной теоремой.

Теорема Абеля. Если степенной ряд (6.5) сходится при некотором значении x x0 , то он сходится, и притом

абсолютно, при всех значениях x , для которых x x0 . Сходимость ряда будет равномерной во всяком интервале

xx1 , где x1 - любое положительное число, меньше, чем x0 .

Если степенной ряд расходится в точке x0 , то он

со всей осью, то существует число R такое, что при x R ряд

степенного ряда.

Для вычисления радиуса сходимости степенного ряда вида (6.5) используется одна из следующих формул:

215

Для нахождения области сходимости степенного ряда нужно найти радиус его сходимости и затем проверить сходимость ряда при x R .

(-1,1). Определим, сходится ли ряд на концах интервала. При

Проверим условие монотонного убывания членов ряда:

сходимости [ 1,1) .

216

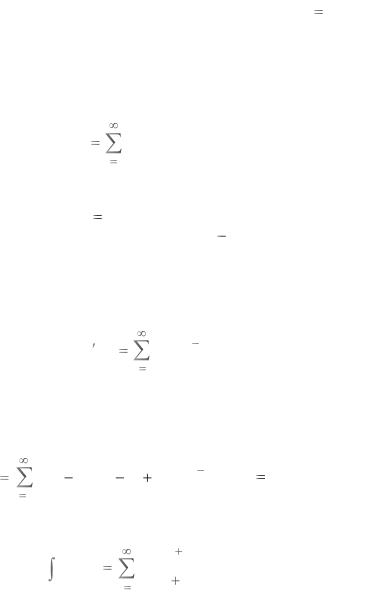
6.4. Свойства степенных рядов

Члены степенного ряда, т.е. функции un (x) an xn ,

являются непрерывными и даже непрерывно дифференцируемыми функциями при любых значениях x . Поэтому из теоремы о равномерной сходимости степенного ряда вытекают следующие его свойства.

1.Сумма степенного ряда

непрерывна в каждой внутренней точке интервала сходимости (здесь и далее предполагается, что интервал сходимости не вырождается в точку x 0 ). Если ряд (6.7) сходится в каком – либо из концов интервала сходимости ( R, R) , то его сумма

будет непрерывной и в этом конце.

2. Степенной ряд (6.7) можно почленно дифференцировать во внутренних точках интервала сходимости, т.е. в них его сумма S(x) дифференцируема и выполняется равенство

причем производный ряд (6.8) имеет тот же интервал сходимости, что и ряд (6.7).

3. Из предыдущего свойства вытекает: сумма степенного ряда (6.7) имеем производные всех порядков, причем

S (m) (x) n(n 1)...(n m 1)an xn m , (m 1,2,...) . (6.9)

nm

4.Степенной ряд (6.7) можно интегрировать почленно в интервале сходимости

причем радиусы сходимости (6.10) и (6.7) совпадает.

217

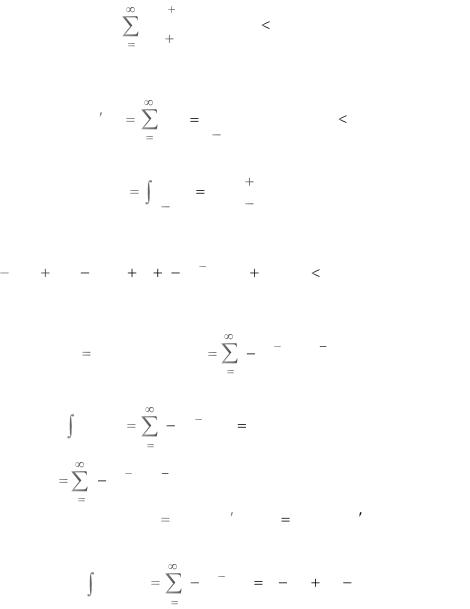
Пример. Используя свойства степенных рядов, найти сумму ряда

218

который не входит в обязательную программу изучения степенных рядов в техническом вузе. Однако для аспирантов и инженеров – исследователей приведенные здесь формулы могут оказаться весьма полезными. Некоторые из этих формул либо вообще отсутствуют в учебной литературе, либо приведены в непригодной для использования форме. Мы приводим также обобщения некоторых известных формул

1. Сложение, вычитание и умножение степенных рядов.

Пусть два степенных ряда

219