
3447
.pdf
y y cos x 0, y(0) 1.
y cos x 0, y(0) 1.
Решение. Воспользовавшись формулой (2.46), получаем:
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
y |
1 exp |
|
( |
cos x)dx |
esin x . |
|
|
|||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
Рассмотрим свойства решений однородного линейного |
||||||||||||||
уравнения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Если |
y1(x) |
есть частное решение уравнения (2.42), то |
||||||||||||
функция y Cy1 , |
где |
C |
- |
произвольная постоянная, тоже |
||||||||||
является решением этого уравнения. |
|
|
|
|
||||||||||
Действительно, |
так как |
y1 - решение уравнения, то имеет |
||||||||||||
место тождество |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
y1 |
p(x) y1 |
|
0 (a x b). |
|
|
||||||
Подставим |
в |
уравнение |
(2.42) |
y |
Cy1 |
и |
примем во |
|||||||
внимание записанное выше тождество. Имеем: |
|
|
||||||||||||
(Cy1) p(x)Cy1 |
|
C( y1 |
p(x) y1) 0 (a x b). |
|||||||||||
Следовательно, |
функция |
y |
Cy1 |
является |
решением |
|||||||||
уравнения (2.42). |
|
|
|
|
|
|
|
|
|
|
|
|
||
2. |
Если |
y1 |
|
- |
частное решение уравнения (2.42), то |
|||||||||
формула y Cy1 , |
где |
C |
- |
произвольная постоянная, дает |
||||||||||
общее |
решение |
|
уравнения |
|
(2.42) |
в |
области |
|||||||
a x |
b, |
|
y |
|
. |
|
|
|
|
|
|
|
|
|
Действительно, |
функция |
y |
Cy1 |
является |
решением |
|||||||||
уравнения (2.42) (как показано выше) для всех значений
параметра C . |
Рассматривая равенство |
y |
Cy1 как уравнение |
||
относительно |
C , |
видим, что оно разрешимо |
в области |
||
a x b, |
y |
при всех C : |
C |
y y1 . |
Поэтому |
формула y Cy1 дает общее решение.
4. В этом разделе рассматривается важнейшее свойство решения неоднородного уравнения – теорема о структуре общего решения линейного неоднородного уравнения.
40

Теорема. Если yчн - частное решение неоднородного
уравнения (2.41), то общее решение дается формулой
|
|
yон |
yоо |
|
yчн , |
|
|
|
|
|
где yоо - общее решение однородного уравнения (2.42) |
||||||||||
|
|
yоо |
|
Ce p(x)dx . |
|
|
|
|
||
Доказательство. Пусть нам известно некоторое частное |
||||||||||
решение yчн неоднородного уравнения |
(2.41), т.е. |
|||||||||
|
yчн |
p(x) yчн |
q(x) |
a x b. |
|
|||||
Введем |
новую |
неизвестную |
|
функцию |
z |
по формуле |
||||
y yчн z . |
Подставляя |
функцию |
y |
в |
уравнение (2.41), |
|||||
получим, требуя, чтобы функция y |
удовлетворяла уравнению: |
|||||||||
|
yчн |
p(x) yчн |
z |
p(x)z q(x). |
|
|||||
Таким образом, чтобы функция |
y |
|
yчн |
z являлась |
||||||
решением (2.41) достаточно, чтобы функция |
z удовлетворяла |
|||||||||
однородному |
линейному |
уравнению, |
и |
соответствующему |
||||||
уравнению (2.41): |
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
p(x)z |
|
0 . |
|
|
|
|
Общее решение этого уравнения, как показано в п.2 настоящего раздела, имеет вид (2.45). Итак, функция z должна
являться общим решением однородного уравнения: |
z yoo . |
||||||
Таким образом, получим: |
|
|
|
|
|
|
|
y yчн |
Ce |
p(x)dx |
( |
C |
). |
|
|
|
|
|
|||||
Покажем, что эта формула представляет общее решение |
|||||||
уравнения (2.41). Запишем это решение в виде |
|
|
|||||
|
|
|
x |
|
|
|
|
|
|
|
|
p(x)dx |
|
|
|
y |
yчн |
Ce |
x0 |
|
|
|
(2.47) |
|
|
|
|
||||
где, как и в формуле (2.45), неопределенный интеграл заменим определенным интегралом с переменным верхним пределом. Покажем, что при любых x0 (a, b) и y0 ( , ) частное
решение уравнения (2.41), удовлетворяющее условию
41
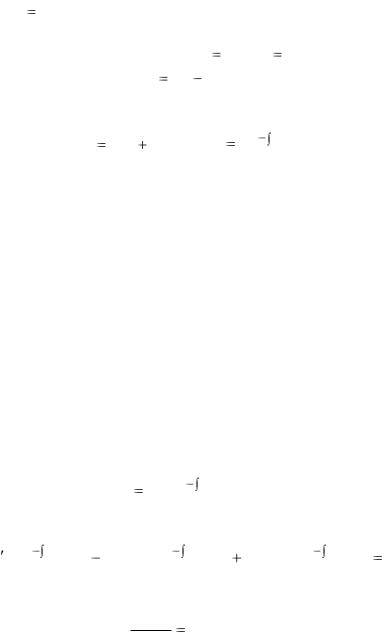
y(x0 ) y0 , принадлежит семейству (2.47) при однозначно
определяемой постоянной C . |
|
|
|
|
||
Полагая в формуле (2.47) |
x |
x0 , y |
y0 , получим: |
|||
|
C |
y0 |
yчн (x0 ) . |
|
|
|
Таким образом, формула (2.47) дает общее решение |
||||||
неоднородного линейного уравнения: |
|
|
||||
|
yон yчн уоо , |
yоо |
Ce |
p(x)dx . |
(2.48) |
|
Итак, для построения общего решения неоднородного |
||||||
линейного |
уравнения |
нужно |
к |
общему |
решению |
|
соответствующего ему |
однородного |
уравнения |
прибавить |
|||
частное решение неоднородного уравнения.
5. Методы построения общего решения неоднородного линейного уравнения.
В настоящем разделе будут рассмотрены два метода решения уравнения (2.41), первый из которых - метод Лагранжа, применяется к решению не только линейных уравнений или сводящимся к ним.
5.1. Метод вариации произвольной постоянной (метод Лагранжа).
Для нахождения решения уравнения (2.41) применим следующий метод: будем искать решение в том же виде, что и решение соответствующего однородного уравнения (2.44), но будем считать C не постоянной, а неизвестной непрерывно дифференцируемой функцией от x . Таким образом, положим
|
|
y C(x)e |
p(x)dx . |
|
|
(2.49) |
Требуем, чтобы функция (2.49) удовлетворяла уравнению |
||||||
(2.41): |
|
|
|
|
|
|
C (x)e |
p(x)dx |
C(x) p(x)e |
p(x)dx |
p(x)C(x)e |
p(x)dx |
q(x). |
|
|
|
||||
Отсюда |
получаем |
следующее дифференциальное |
||||
уравнение, которому должна удовлетворять функция C(x) :
dC(x) q(x)e p(x)dx . dx
p(x)dx . dx
42

Это уравнение – простейшее дифференциальное уравнение с разделяющимися переменными. Интегрируя его, имеем:
dC(x) |
q(x)e p(x)dx dx C, C(x) |
C q(x)e p(x)dx dx , |
||
где C - произвольная постоянная ( |
C |
) . |
Подставляя |
|
эту функцию в формулу (2.49) получим: |
|
|
|
|
y e |
p(x)dx C q(x)e p(x)dx dx , |
( |
C |
). (2.50) |
Полученная функция по построению является решением уравнения (2.41). Более того, она является общим решением в
полосе |
a |
x |
b, |
y |
, поскольку имеет |
структуру |
(2.48). |
|
|
|
|
|
|
Действительно, записав (2.50) в виде |
|
|||||
|
y |
Ce |
p(x)dx |
e |
p(x)dx q(x)e p(x)dx dx, |
(2.51) |
заметим, что первый член в правой части является общим решением соответствующего однородного уравнения, а второе слагаемое есть частное решение неоднородного уравнения, так как оно содержится в формуле (2.51) при C 0 .
Формула (2.51) показывает, что общее решение линейного неоднородного уравнения можно получить двумя квадратурами.
Отметим характерное свойство решения линейного уравнения. Из (2.51) видно, что общее решение линейно зависит от произвольной постоянной. Для нелинейных уравнений такое свойство уже не выполняется.
Другой вид общего решения получается из (2.51) заменой неопределенных интегралов определенными с переменным верхним пределом:
x |
x |
s |
|
|
p(t)dt |
p(t)dt x |
|
p(t)dt |
|
y Ce x0 |
e x0 |
q(s)e x0 |
ds, |
(2.52) |
|
x0 |
|
|
|
где x0 - произвольное число из (a,b) , x (a,b) .
43

Пусть требуется решить задачу Коши для уравнения
(2.41), то есть нужно найти такое решение уравнения, которое
удовлетворяет |
|
условию |
y(x0 ) |
y0 , |
где |
|
x0 (a, b) , |
||||||
y0 |
( |
, |
) . |
|
Подставляя в |
(2.52) |
x x0 , |
y |
y0 |
находим: |
|||
C |
y0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, решением задачи Коши является функция |
||||||||||||
|
|
|
|
|
|
x |
|
x |
s |
|
|
|
|
|
|
|
|
|
|
p(t)dt |
|
p(t)dt x |
p(t)dt |
|
|
|
|
|
y |
y |
0 |
e |
x0 |
e |
x0 |
q(s)e x0 |
|
ds. |
(2.53) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
|
|
|
|
|
З а м е ч а н и е 1. Формула (2.52) показывает, что если |
||||||||||||
функции |
|
p(x) |
и q(x) |
заданы и непрерывны |
на |
всей |
оси |
||||||
( |
, ) , |
то и решение с любыми начальными данными x0 , |
y0 |
||||||||||
будет не только непрерывно, но и непрерывно дифференцируемо при всех значениях x . Это означает, что интегральная кривая уравнения, проходящая через любую точку плоскости M 0 (x0 , y0 ) будет гладкой кривой при
x ( , ) .
За м е ч а н и е 2. Если функции p(x) и q(x) непрерывны
в(a,b) , за исключением отдельных точек, то формула общего
решения (2.51) или (2.52) остается справедливой для всех x из (a,b) , если интегралы при переходе через точки разрыва не
теряют смысл (если интегралы расходятся, то формула общего решения уже не будет справедливой во всем интервале).
Пример. |
|
Найти общее решение |
дифференциального |
||
уравнения y |
|
2 |
y |
x. |
|
|
|
|
|||
|
|
x |
|
|
|
Решение. Данное уравнение является уравнением вида |
|||||
(2.41), где |
p(x) |
2 x , q(x) x , |
то есть линейным |
||
неоднородным уравнением. Функция q(x) определена и непрерывна при всех x , а функция p(x) - при
44

x ( ,0) (0, ) . Найдем его общее решение методом вариации постоянной.
Решим соответствующее |
ему |
однородное |
z |
2 |
z 0. |
||||||||||||
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
Разделяя переменные и интегрируя, |
получим |
|
|
|
|||||||||||||
|
dz |
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
, |
ln |
z |
|
ln |
C |
|
2 ln |
x |
( C |
0 ), |
|
|
|||
|
|
|
|
|
|
||||||||||||
|
z |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
||
откуда z Cx2 |
(C |
0) и z |
0 . Общее решение имеет вид |
||||||||||||||
|
|
|
|
|
z |
Cx 2 , C ( |
, ) . |
|
|
|
|
||||||
Общее решение неоднородного уравнения, в соответствии |
|||||||||||||||||
с методом Лагранжа, ищем в виде y |
C(x)x2 . |
|
|
|
|||||||||||||
Находим производную y C (x)x2 2xC(x) , которую, вместе с функцией y подставляем в уравнение. Получаем:
C (x)x2 2xC(x) , которую, вместе с функцией y подставляем в уравнение. Получаем:
C (x)x2 2xC(x) |
|
2 |
|
C(x)x2 |
x |
|
|
|||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
dx |
|
|
|
|
C . |
|
|||||||
C (x) |
, |
|
dC(x) |
|
, C(x) ln |
x |
|
|||||||||||||
|
|
|
||||||||||||||||||
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Подставляя найденную функцию в выражение для общего |
||||||||||||||||||||
решения, получим окончательно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
y x 2 (C |
|
|
|
|
|
|
|
|
||||||||
|
|
|
ln |
x |
) . |
|
|
|
|
|
|
|||||||||
Пример. Найти общее решение уравнения xy |
2x2y |
1, |
||||||||||||||||||
пользуясь формулой общего расчета (2.50). |
|
|
|
|
|
|
||||||||||||||
Решение. |
|
В |
данном |
случае |
p(x) |
2x , |
q(x) |
1 x . |
||||||||||||
Подставляя в формулу (2.51), получим: |
|
|
|
|
|
|
|
|||||||||||||
y e 2xdx |
C |
|
1 |
e 2xdx dx |
|
|
|
|
e |
x 2 C |
|
|
e x 2 |
dx . |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
45
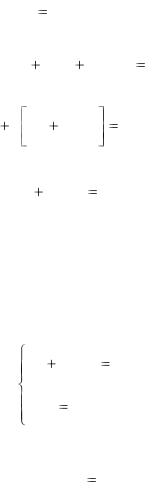
Отметим, что интеграл, содержащийся в записанном общем решении не выражается в конечном виде через элементарные функции.
5.2. Метод Бернулли построения общего решения.
Другим по форме, но идентичным по существу, является метод Бернулли, в соответствии с которым решение неоднородного линейного уравнения ищется в виде произведения двух функций
|
|
|
|
y u(x)v(x) . |
(2.54) |
||||||
Подставляя (2.54) в уравнение (2.41), получим: |
|
||||||||||
|
|
v |
du |
|
u |
dv |
|
p(x)uv q(x) , |
|
||
|
|
dx |
dx |
|
|||||||
|
|
|
|
|
|
|
|
||||
или |
|
|
|
|
|
|
|
|
|
|
|
v |
du |
|
u |
dv |
|
p(x)v q(x). |
(2.55) |
||||
dx |
|
dx |
|
||||||||
|
|
|
|
|
|
|
|
|
|||
Функцию v(x) выбираем так, чтобы |
|
||||||||||
|
|
|
|
dv |
p(x)v |
0. |
(2.56) |
||||
|
|
|
|
|
|
|
|||||
|
|
|
|
dx |
|||||||
|
|
|
|
|
|
|
|
|
|||
Это означает, что на одну из двух функций налагается требование – она должна удовлетворять однородному уравнению, соответствующему данному неоднородному. Таким образом, дифференциальное уравнение (2.55) будет равносильно системе двух дифференциальных уравнений, одно из которых – уравнение (2.56), а другое получается из (2.55) при условии (2.56). Имеем:
dv |
p(x)v 0, |
|||
|
|
|
||
dx |
||||
(2.57) |
||||
|
du |
|||
v |
q(x). |
|||
dx |
||||
|
|
|||
Оба уравнения системы (2.57) являются уравнениями с разделяющимися переменными. Для первого из них мы
возьмем частное решение v exp( p(x)dx) (см. формулу (2.48)). Из второго уравнения получаем
p(x)dx) (см. формулу (2.48)). Из второго уравнения получаем
46
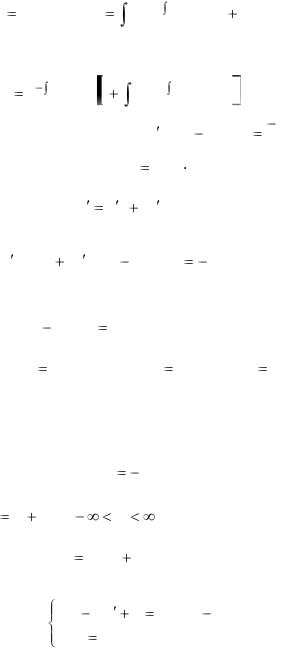
du |
|
q(x) |
dx , |
u |
q(x)e p(x)dx dx C. |
|
|
|
|||||
|
|
|
|
|
|||||||||
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
Подставив найденные функции v(x) |
и u(x) |
в формулу |
|||||||||||
(2.54), получим общее решение уравнения |
|
|
|
|
|
|
|||||||
|
y e |
p(x)dx C |
q(x)e p(x)dx dx . . |
|
|
|
|||||||
Пример. |
Решить уравнение |
y sin x |
y cos x |
sin |
2 x |
. |
|||||||
x2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Ищем его в виде y |
u(x) v(x) . Дифференцируя |
||||||||||||
по х, имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
u v |
|
uv . |
|
|
|
|
|
|
Подставим эти выражения в уравнение |
|
|
|
|
|
|
|||||||
u v sin x |
uv sin x |
uv cos x |
|
sin2 x |
|
|
|
(*) |
|||||
|
x2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
и потребуем, чтобы функция v(x) удовлетворяла однородному
уравнению |
dv |
sin x |
v cos x |
0 . |
|
|
|
|
|||
|
|||||||||||
|
dx |
|
|
|
|
|
|
|
|||
|
|
|
dv |
cos x |
|
|
|
|
|
||
Отсюда |
|
|
dx , |
ln |
v |
ln |
sin x |
, v sin x . |
|||
|
|
|
|
|
|||||||
|
|
|
v |
sin x |
|
|
|
|
|
||
Подставим функцию v в уравнение (*) и учитывая равенство нулю подчеркнутой части, получим уравнение для u(x)
|
|
|
du |
sin2 x |
|
sin2 x |
. |
||
|
|
|
|
|
|||||
|
|
|
dx |
|
|
|
x2 |
||
Отсюда u(x) |
1 |
C , |
C |
|
и, таким образом, |
||||
|
|
||||||||
x |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
sin x |
C sin x . |
||||
|
|
|
|
|
|||||
|
|
|
x |
||||||
|
|
|
|
|
|
|
|
||
Пример. Найти решение задачи Коши |
|||||||||
|
|
|
x(x |
1) y |
y x 2 (2x 1), |
||||
|
|
|
y(2) |
4. |
|
|
|
|
|
47

Решение. Ищем общее решение дифференциального
уравнения |
методом Бернулли |
y |
uv . |
Подставляя y и |
y u v uv |
в уравнение, получим: |
|
|
|
|
x(x 1)(u v uv ) |
uv |
x2 (2x |
1) , |
|
x(x 1)u v u x(x 1)v v x2 (2x 1) . |
|||
Налагаем требование на функцию v(x) - равенства нулю
выражения в квадратных скобках. Получаем систему дифференциальных уравнений
|
|
x(x |
|
1) |
|
dv |
|
|
|
v |
0, |
|
|
|
|
|
|
|
|
||||||
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x(x |
|
1)v |
du |
|
|
x2 |
(2x |
1). |
|
|
|
||||||||||||
|
|
|
dx |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решаем первое уравнение, разделяя переменные |
|||||||||||||||||||||||||
|
dv |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
dx |
|||||||
|
|
|
|
|
|
|
|
, |
|
ln v |
|
|
|
|
|
|
|
. |
|||||||
|
v |
|
|
x(x 1) |
|
|
|
|
|
x(x 1) |
|||||||||||||||
Разлагаем подынтегральную |
правильную рациональную |
||||||||||||||||||||||||
дробь на сумму простых дробей: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
A |
|
B |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
x(x 1) |
|
|
|
x |
|
x 1 |
|
|
|
|
|
|
||||||||||
откуда A(x 1) |
Bx 1. |
|
Полагая |
|
x |
0 , |
|
получим A 1; |
|||||||||||||||||
полагая x 1, получим B |
|
1. Таким образом, имеем: |
|||||||||||||||||||||||
|
|
ln v |
dx |
|
|
dx |
|
ln |
|
|
|
x |
|
. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
x |
|
x |
1 |
|
x |
1 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||
Частное решение берем в виде v |
|
|
|
|
. Подставляя эту |
||||||||||||||||||||
|
x |
|
1 |
||||||||||||||||||||||
функцию во второе уравнение системы, получим:
x |
2 du |
x |
2 |
(2x |
1) , |
du (2x |
1)dx, |
u |
|
x |
2 |
x C. |
||||
|
dx |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общее решение имеет вид |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
y |
|
x |
|
(x2 |
x C) |
x2 C |
x |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
x |
|
1 |
|
|
x |
1 |
|
|
||
48

|
Для построения решения задачи Коши найдем значение |
|||||||||||||||||||||||||
C , используя начальное условие |
x0 |
2, |
y0 |
|
|
|
4. Имеем: |
|||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
4 C |
2 |
, |
C |
|
|
0 . |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решением задачи Коши является функция y |
|
|
x2. |
|
||||||||||||||||||||||
|
|
|
Задачи для самостоятельного решения |
|
||||||||||||||||||||||
1. |
y |
ytgx |
xtgx |
1, |
y(0) |
1. |
|
Ответ: |
y |
|
|
C sin x |
x . |
|||||||||||||
2. |
y sin2x |
2( y cosx) . |
Ответ: |
y |
|
|
ctg x |
|
|
1 |
|
. |
|
|||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
cos x |
|
||||||||||||||||||||||
3. |
y |
2xy |
3x2 |
2x4 , |
y(0) |
1. |
Ответ: y |
|
e x2 . |
|
||||||||||||||||
4. |
dx |
(x y)dy 0. |
|
|
Ответ: x |
Ce y |
|
|
y 1. |
|
||||||||||||||||
5. |
y |
ytgx |
2sin x, |
|
y(0) |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Ответ: |
y |
|
|
1 |
(C |
cos2 x), |
y |
|
|
cos x . |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
cos x |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6. |
e x ( y |
y) |
|
1. |
|
|
|
Ответ: y |
e |
x (x |
C). |
|
||||||||||||||
7. |
x2 y |
2xy |
ln x |
0. |
Ответ: |
y |
|
ln x |
1 |
|
|
|
|
C |
. |
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
x2 |
|
||
8. |
y |
y |
sin x. |
|
|
|
Ответ: |
y |
|
Ce x |
|
|
1 |
(cosx |
sin x). |
|||||||||||
|
|
|
|
|
|
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2.5. Уравнение Бернулли |
|
|
|
|
|
|
|
|||||||||||||
|
Уравнение вида |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
y |
|
p(x) y |
|
q(x) yv , |
|
|
|
|
|
|
|
|
|
(2.41) |
|||||
где |
v |
- любое действительное число, |
называется уравнением |
|||||||||||||||||||||||
Бернулли. |
Если |
v |
0 , |
то уравнение Бернулли вырождается в |
||||||||||||||||||||||
линейное уравнение (2.41); при v |
1 уравнение превращается в |
|||||||||||||||||||||||||
уравнение с разделяющимися переменными: |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
y |
|
p(x)y |
|
q(x) |
(v |
0); |
|
|
|
|
|
|
|
|
|||||
49
