3447

dФ(x)

A(x)Ф(x) ,

(5.37)

dx

дифференцировании

произведения матриц

необходимо

сохранять

порядок

сомножителей

-

(A(x)B(x))

A (x)B(x) A(x)B (x) .

Общее решение однородной линейной системы

дифференциальных уравнений.

Как

и

в

случае

однородного

линейного

дифференциального

уравнения

n -го порядка,

знание

общее

решение

однородной

линейной

системы

дифференциальных уравнений.

Теорема 6 (об общем решении). Если система функций

y11 ,

y12 ,

y1n,

y21,

y22,

y2n ,

(5.38)

yn1,

yn2,

ynn

y1 (x)

C1 y11

C2 y21 Cn yn1,

y2 (x)

C1 y21

C2 y22

Cn yn2 ,

(5.39)

yn (x)

C1 yn1

C2 yn2

Cn ynn ,

или в сокращенной форме

n

yk (x) Ci yik (x),

(k 1,2,..., n),

(5.40)

i 1

(где C1, C2 ,..., Cn

произвольные

постоянные) дают общее

решение системы (5.23) в области

a

x

b,

yk

(k

1,2,..., n) .

(5.41)

*Замечание. В векторной форме теорема формулируется

так:

если

система

вектор

-

функций

решений

Yk (x)

colon(yk1, yk 2 ,..., yk n)

(k

1,2, n.)

. является. ,

однородного

уравнения

Y

A(x)Y ,

то вектор-функция

n

Y (x)

colon(y1, y2 ,..., yn ) ,

где

ym (x)

Ci yim

дает общее

i 1

решение

этого

уравнения

в

области

a x

b,

ym

(m 1,2,..., n) .

Доказательство. Совокупность функций (5.39) является

решением системы (5.23)

при

всех значениях

постоянных

y1 y1(0) , y2 y2(0) ,..., yn yn(0) при x x0 ,

(5.42)

включаться

в

решение

(5.39)

при

C

C(0) ,C

2

C

(0)

,..., C

n

C(0) .

1

1

2

n

Действительно, полагая в (5.39) x

x0 , учитывая (5.42)

получим

y(0)

C ( y

)

0

C

2

( y

21

)

0

C

n

( y

n1

)

0

,

1

1 11

y(0)

C ( y

)

C

( y

)

C

n

( y

2n

)

,

(5.39)

2

1

21

0

2

22

0

0

y(0)

C ( y

n1

)

0

C

2

( y

n2

)

0

C

( y

)

0

,

n

1

n

nn

где

( yij )0

yij (x0 ).

Полученная

система

линейных

неоднородных

уравнений

относительно

неизвестных

C1 , C2 ,..., Cn

имеет единственное решение, поскольку ее

определитель

равен W (x0 ) -

вронскиану

фундаментальной

системы функций (5.38) при x

x0 , которой отличен от нуля.

Поэтому

C

C (0) (x

0

, y(0)

,..., y

(0) ), C

2

C (0) (x

0

, y(0)

,..., y (0) ),...,

1

1

1

n

2

1

n

(5.44)

C (0) (x

, y(0) ,..., y(0) ).

C

n

0

n

1

n

Подставляя эти значения постоянных в общее решение

(5.39) найдем решение задачи Коши (5.23), (5.42).

Таким образом, чтобы линейная комбинация n решений

однородной

линейной

системы (5.23)

с

произвольными

постоянными C1 , C2 ,..., Cn

давала

общее

решение этой

Y(x) Ф(x)C,

(5.45)

где

Y (x)

colon(y1 (x), y2 (x),..., yn (x)) ,

yk (x) - функции из

(5.39),

Ф(x) -фундаментальная

матрица

(5.36),

C

colon(C1, C2 ,..., Cn ) - постоянный вектор с произвольными

координатами.

Если положить в (5.45) x x0 , получим Y (x0 )

Ф(x0 )C .

Отсюда,

поскольку матрица Ф(x0 )

не вырождена, имеем

C

Ф 1(x0 )Y (x0 ) . Подставляя C в формулу (5.45), получаем

Y (x) Ф(x)Ф(x0 )Y (x0 ) .

(5.46)

K(x, x

)

Ф(x)Ф 1(x )

(5.47)

0

0

Y (x) K (x, x0 )Y (x0 ) .

(5.48)

Пример. Найти общее решение линейной однородной

системы

dy

(x x 2 ) y (x3

x 2

x 1)z,

dx

dz

(1 x) y (x 2

x 1)z.

dx

y (x)

a b x c x2 ,

z (x)

a

2

b x .

1

1

1

1

1

2

Подставляя

y1(x) и z1 (x) в уравнения заданной системы

и приравняв коэффициенты при одинаковых степенях

x ,

получим уравнения для определения коэффициентов:

c1

b2

0, c1

b1

a2

b2

0, b1

a1

a2

b2 0,

a1

c1

a2 2c1

0,

b1

a2 , a1

a2

b2

0.

Уравнения удовлетворяются, если b1

a2

0, a1

b2

c1.

Полагая a1

b2

c1

1,

находим одно решение системы:

y

x2

1,

z

x.

1

1

Второе решение системы будем искать в виде

y

2

( A B x)e x ,

z

2

( A B

2

x)e x .

1

1

2

A1 B1

A2 ,

A1

B2 A1

B2 ;

B1

A1

A2

B2 ,

B2

A1

B1

A2

B2 ;

0

A1

B1

A2

B2 ,

0

B1

A2

B2 ; 0

B1

A2 ,

0 B2 .

Уравнения удовлетворяются, если B2

A1

0 ,

A2

B1 1.

Поэтому, второе решение системы имеет вид

y2

xex ,

z2

e x .

W (x)

x 2

1 xex

e x

0 .

x

e x

y C y

1

C

2

y

2

C (x2

1) C

2

xex ,

1

1

z C z

1

C

2

z

2

C x C

e x .

1

1

2

dyk

n

ak i (x) yi

fk (x), (k 1,2,..., n) ,

dx

i 1

dY

A(x)Y F,

L[Y ]F.

dx

Установим наиболее важные свойства решений

линейной неоднородной системы.

Теорема

7

(принцип

суперпозиции).

Пусть

m

F (x)

i Fi (x),

где

i -

постоянные

числа,

i 1

F (x)

colon( f

(i) (x),..., f (i) (x)) ,

и

пусть

Y (x)

-

решение

i

1

n

i

уравнения Yi

A(x)Yi

Fi (x) . Тогда вектор-функция

m

Y (x)

iYi (x)

i 1

d m

m

m

dY

m

L[Y ]

iYi A(x)

iYi

i

i

A(x)Yi

i Fi .

dx i 1

dx

i 1

i 1

i 1

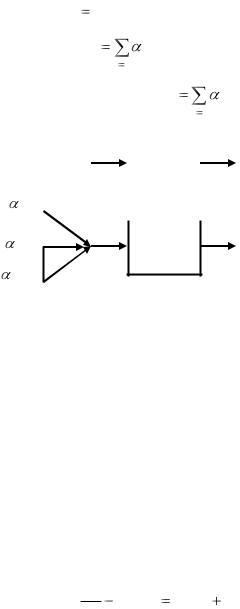
сигнал Yk (x)

(k 1,2,..., m) . Если

на вход такой системы

m

подать сигнал

F(x)

i Fi (x) , то на выходе из устройства

i 1

m

будет наблюдаться сигнал Y (x)

iYi (x) (рис.11).

i 1

Fk (x)

L

Yk (x)

1F1

2 F2

L

Y (x)

где i

-

мнимая

единица,

F1 (x)

colon(u1 ,..., un ) ,

F2 (x)

colon(v1 ,..., vn )

с

действительными

функциями aij (x) ,

ui (x) ,

vi (x) (i, j

1,2,..., n) имеет решение

Y (x)

Y1(x) Y2 (x),

Y (x)

colon(y(1)

,..., y(n) ) ,

Y (x) colon(y(1)

,..., y(n) ),

то

1

1

1

2

2

2

действительная

часть

решения

Y1 (x)

и

его мнимая часть

Y2 (x) соответственно являются решениями уравнений

dY1

A(x)Y1

F1 (x) ,

dY2

A(x)Y2

F2 (x) .

dx

dx

Доказательство.

По условию L[Y ]

F1

iF2 , где

L -

линейный

оператор

(5.23).

Докажем,

что

L[Y1 ]

F1 ,

L[Y2 ]

F2 . Действительно,

в силу линейности оператора

L ,

получаем

L[Y1

iY2 ]

L[Y1] iL[Y2 ]

F1

iF2 .

Учитывая определение равенства комплексных чисел,

имеем L[Y1 ]

F1 ,

L[Y2 ]

F2 .

Теорема 9.

Если Y (n) (x)

является решением линейной

неоднородной системы

L[Y]

F ,

(5.41)

L[Y]

, то сумма Y (n) (x) Y (0) (x)

также будет решением

неоднородной системы (5.49).

Доказательство.

По условию теоремы

L[Y (n) ]

F и

L[Y (0) ]

,

где

- нулевой

вектор.

Покажем,

что

L[Y (n)

Y (0) ]

F . Действительно,

используя линейность

оператора L , будем иметь:

L[Y (n) Y (0) ]

L[Y (n) ] L[Y (0) ] F

F.

(5.49) с непрерывными на [a,b]

коэффициентами aij (x) и

непрерывными правыми частями

fi (x) равно сумме общего

n

решения

Yoo (x)

CiYi , соответствующей неоднородной

i 1

системы ( Yi (x)

- линейно независимые решения однородной

системы)

и частного решения

Yчн (x) рассматриваемой

dyk

fk (x, y1,..., yn )

(k

1,2,..., n),

dx

с

начальными

условиями

yk (x0 )

yk 0 ,

являются:

непрерывность всех

функций f k

в окрестности

начальных

данных

и

ограниченность

fk

.

Очевидно,

что для

yk

нормальной

линейной системы

с непрерывными aij (x)

и

fi (x) эти условия выполняются при

x [a,b] .

Поэтому для

доказательства

сформулированной

теоремы

достаточно

показать,

что

подбором

постоянных

Ci

в

решении

n

Y

CiYi

Yчн

можно удовлетворить произвольно заданным

i 1

начальным условиям Y (x0 )

Y0

colon(y10 , y20 ,..., yn0 ) .

Покажем, что векторное уравнение

n

CiYi (x0 ) Yчн (x0 ) Y0

i

1

или

эквивалентная

система

алгебраических

линейных

по

Ci (i

1,..., n) уравнений

n

Ci y1i (x0 )

yчн1 (x0 )

y10 ,

i

1

n

Ci y2i (x0 )

yчн2 (x0 ) y20 ,

(5.50)

i

1

n

Ci yni (x0 )

yчнn (x0 )

yn0

i

1

имеет

решение C(0) ,..., C(0) , при

любых

правых частях

1

n

yk 0

yчнк (x0 )

системы (5.50). Но определитель этой системы

равен определителю Вронского в точке x

x0 . Для линейно

независимых

решений

Y1,Y2 ,..., Yn

соответствующей

однородной системы он

отличен

от нуля. Следовательно,

Пусть известна

фундаментальная система решений для

соответствующей

однородной

системы

уравнений

Y (x) A(x)Y (x) .

Тогда общее решение неоднородной

системы уравнений

Y (x) A(x)Y(x)

F(x) может быть

найдено с помощью квадратур.