
3447
.pdf
В результате исключения неизвестной функции y из одного уравнения пришли к следующим уравнениям
|
d |
2 z |
2 |
dz |
z 0, y |
1 |
|
dz |
z . |
|
dx2 |
dx |
2 |
|
dx |
||||
|
|
|
|
|
|||||
Первое из |
уравнений является линейным однородным |
||||||||
дифференциальным уравнением второго порядка с постоянными коэффициентами. Его решение (см. гл. 4) ищем
в виде z |
ek x . Подставляя |
эту |
функцию в уравнение, |
|
получим: |
k 2 2k 1 0, k |
k |
2 |
1. Характеристическое |
|
1 |
|
|
|
уравнение имеет кратный корень. В этом случае линейно
независимые частные решения имеют вид |
z e x , z |
2 |
xex . |
|
1 |
|
Следовательно, общее решение первого уравнения
записывается так: |
z e x (C |
xC |
2 |
) . Подставим эту функцию |
|
1 |
|
|
во второе уравнение, получим:
z |
1 |
e |
x |
(2C |
C |
|
2C |
|
x) . |
|
|
2 |
2 |
||||||
|
|
|
|
1 |
|
|
|
2
Задачи для самостоятельного решения
Решить системы уравнений
1. y y2 sin x, z |
y |
. Ответ: |
|
2z |
|||
|
|
2. y1 y2 , y2 y1, y3 y1 y2 y3 .
3. y 2y z, z
2y z, z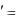 y. Ответ:
y. Ответ:
4. y ay z, z
ay z, z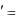 y az. Ответ:
y az. Ответ:
y |
C e x |
C |
e x |
1 |
cos x, |
|
||||
|
|
|
||||||||
|
1 |
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
z 2 |
C e x |
C |
e x |
|
1 |
sin x. |
||||
|
|
|||||||||
|
1 |
|
2 |
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
y |
C e x |
C |
e x |
, |
|||||
|
1 |
|
|
1 |
2 |
|
|
|||
Ответ: |
y |
2 |
|
C e x |
|
C |
e x , |
|||||||
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
||
|
|
y |
3 |
|
C |
e x |
|
|
2C xex . |
|||||
|
|
|
|
|
3 |
|
|
|
|
|
|
1 |
||
y |
(C |
|
|
C |
2 |
x)e x |
, |
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
e x (C |
2 |
x |
|
C |
|
|
C |
2 |
). |
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
y |
eax (C cos x |
|
|
C |
2 |
sin x), |
||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
z |
eax ( |
|
C sin x |
|
C |
2 |
cos x). |
|||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
170
5.4. Нормальные системы линейных дифференциальных уравнений
В §5.1 дано определение нормальной линейной системы дифференциальных уравнений и приведен вид системы (5.4). В дальнейшем уравнения (5.4) будем записывать в сокращенном виде:
|
dyi |
n |
|
|
|
|
|
aij (x) y j |
fi (x), (i 1,2,..., n) |
(5.21) |
|||
|
dx |
|||||
|
j 1 |
|
|
|
||
|
|
|
|
|
||
или в векторной (матричной) форме |
|
|||||
|
|
|
dY |
A(x)Y F(x) , |
(5.22) |
|
|
|
|
|
|||
|
|
|
dx |
|||
|
|
|
|
|
|
|
где Y и F n - мерные векторы, A - матрица коэффициентов системы
a11(x) a12 (
Aa21(x) a22 (
an1(x) an2 (
x) |
an1(x) |
|
|
x) |
a1n (x) |
, |
|
|
|
|
|
|
|
||
x) |
|
ann (x) |
|
Y colon(y1, y2 ,...., yn ) , F colon( f1, f2 ,...., f n ) , где символ
“colon” - обозначает матрицу-столбец.
Используя правило умножения матриц и определение равенства матриц легко убедиться в том, что уравнение (5.22) равносильно системе уравнений (5.21).
Если все функции aij (x) и fi (x) в (5.21) непрерывны на
отрезке a x b , то в достаточно малой окрестности каждой точки M 0 (x0 , y1(0) ,..., yn(0) ) , где a x0 b , выполнены
условия теоремы существования и единственности (см. §5.2). Следовательно, через каждую такую точку проходит единственная интегральная кривая системы (5.21). Это вытекает из того, что правые части системы (5.21) непрерывны, а их частные производные по любому y j
171

ограничены, т.к. эти |
производные равны |
непрерывным |
на |
|||||||||||||||||||
[a,b] коэффициентам aij (x) . |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Если |
все |
функции |
|
|
fi (x) |
0 |
|
(i 1,2,..., n) , |
т.е. |
||||||||||||
|
F(x) |
colon(0,0,...,0) , то система |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
dyi |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aij (x) yi |
|
|
|
|
|
(5.23) |
||||
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
называется |
линейной |
|
|
однородной. |
В |
векторной |
записи |
|||||||||||||||
линейная однородная система имеет вид |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
dY |
|
|
A(x)Y. |
|
|
|
|
|
(5.24) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для |
изучения |
|
|
|
|
|
свойств |
|
|
линейных |
систем |
||||||||||
дифференциальных уравнений введем линейный оператор |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
L |
|
|
d |
A. |
|
|
|
|
|
(5.25) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда однородное уравнение (5.24) можно записать в виде |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
L[Y] |
|
|
, |
|
|
|
|
|
(5.26) |
||||
где |
colon(0,0,....,0) |
|
|
- нулевой вектор, а соответствующее |
||||||||||||||||||
неоднородное уравнение (5.22) |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
L[Y] F |
|
|
|
|
|
(5.27) |
|||||||
|
Линейность оператора L означает, |
что выполняются два |
||||||||||||||||||||
свойства: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
однородность - |
L[ Y] |
|
|
L[Y] , |
где |
- |
произвольная |
||||||||||||||
постоянная; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
аддитивность |
L[Y1 |
Y2 ] L[Y1] |
L[Y2 ], |
где |
Y1, Y2 - |
||||||||||||||||
дифференцируемые n -мерные векторы. |
|
|
|
|
|
|||||||||||||||||
|
Эти свойства легко проверяются для оператора (5.25). |
|||||||||||||||||||||
Действительно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
d ( Y ) |
A( Y ) |
C |
dY |
|
|
AY , |
|
|
|
|
|
|
|
|
|||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d (Y1 |
Y2 ) |
A(Y1 |
Y2 ) |
|
|
|
dY1 |
|
|
AY1 |
|
dY2 |
AY2 . |
|
|
||||||
|
dx |
|
|
|
|
|
|
dx |
|
|
|
|
dx |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
172

Из этих свойств вытекает:
|
m |
m |
L |
iYi |
i L Yi , где i - произвольные постоянные. |
i |
n |
i 1 |
|
2. Свойства решений линейной однородной системы. |
|
Основной проблемой при решении неоднородных систем (5.21) является построение решений соответствующей однородной системы (5.23). Ниже будет показано, что интегрирование неоднородной системы сводится к интегрированию однородной. В этом разделе займемся изучением однородной системы линейных дифференциальных
уравнений. |
|
|
|
|
Теорема 1. |
Если Y (x) является решением |
линейной |
||
однородной системы (5.26) (или (5.24)), то |
cY (x) |
является |
||
решением этой системы ( c - произвольная постоянная). |
|
|||
Доказательство. Поскольку L[Y] |
по условию, |
то в |
||
силу линейности оператора L имеем: L[cY ] |
cL[Y] |
|
|
|
Теорема 2. |
Сумма Y1 Y2 двух решений |
Y1 и |
Y2 |
|
однородной линейной системы уравнений (5.26) является решением этой системы.
Доказательство. |
Так |
как |
по |
условию |
L[Y1] |
, |
|
L[Y2 ] |
, то L[Y1 Y2 ] |
L[Y1] |
L[Y2 ] |
, где использовано |
|||
свойство аддитивности оператора L . |
|
|
|
|
|||
С л е д с т в и е теорем 1 и 2. Линейная комбинация |
|||||||
k |
|
|
|
|
|
|
|
ciYi |
решений Y1,..., Yk |
системы |
(5.26) с произвольными |
||||
i 1 |
|
|
|
|
|
|
|
постоянными коэффициентами |
c1,..., ck |
является |
решением |
||||
этой линейной однородной системы.
При решении однородного линейного дифференциального уравнения n - го порядка мы использовали комплексные решения для построения его действительных решений. Аналогичная ситуация складывается и при решении линейных однородных систем дифференциальных уравнений.
173

Приведенная ниже теорема позволяет отыскать действительные решения системы из известных комплексных
решений. |
|
|
|
|
|
|
|
|
|
|
|
Теорема 3. |
Если |
линейная однородная система (5.23) с |
|||||||||
действительными |
коэффициентами |
aij (x) |
имеет |
||||||||
комплексное решение Y Y1 |
|
iY2 , то действительная Y1 |
и |
||||||||
мнимая Y2 |
части в отдельности |
|
|
|
|
|
|||||
Y1 |
colon(y11, y21,..., yn1) , |
Y2 |
colon(y12 , y22 ,..., yn2 ) |
|
|||||||
является решениями этой системы. |
|
|
|
|
|
||||||
Доказательство. |
Поскольку |
|
L[Y1 |
iY2 ] |
, |
то |
|||||
используя |
линейность |
|
оператора |
|
L , |
имеем: |
|||||
L[Y1 |
iY2 ] |
L[Y1] |
iL[Y2 ] |
. |
Так |
как |
два |
комплексных |
|||
выражения равны между собой тогда и только тогда, когда равны соответственно их вещественные и мнимые части, то
видим: L[Y1] |
, |
L[Y2 ] |
. |
Таким |
образом, |
Y1 |
и |
Y2 |
|||||
являются решениями системы. |
|
|
|
|
|
||||||||
|
Пример. Дана однородная система линейных уравнений: |
||||||||||||
|
|
|
|
|
dy1 |
|
y2 , |
|
|
|
|
||
|
|
|
|
|
|
dx |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
dy2 |
|
y1. |
|
|
|
|
||
|
|
|
|
|
|
dx |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
Нетрудно |
проверить, |
что |
функции y1 |
cos x |
i sin x , |
|||||||
y2 |
sin x |
i cos x |
являются |
решением этой |
системы. |
||||||||
Проверка |
же |
показывает, |
что |
функции |
y11 |
cos x , |
|||||||
y21 |
sin x , а |
также функции |
y12 |
sin x , |
y22 cos x |
являются решениями этой системы. |
|
|
|
||
|
Допустим, |
что мы нашли |
n |
частных |
решений |
однородной системы (5.23). Основной вопрос заключается в следующем: при каком условии линейная комбинация этих решений с произвольными постоянными коэффициентами c1,..., cn даст общее решение однородной системы?
174

Для ответа на поставленный вопрос введем понятие о линейной независимости систем функций.
Рассмотрим m систем функций:
y11 , |
y12 , |
y1n; |
|
y21, |
y22, |
y2n ; |
|
|
|
|
(5.28) |
|
|||
ym1, |
ym2, |
|
ymn . |
Эти системы функций называются линейно независимыми в интервале (a,b) , если не существует чисел
1, 2 ,..., m не равных нулю одновременно, при которых для всего интервала (a,b) выполнялись бы соотношения:
1 y11 |
2 y21 |
m ym1 |
0, |
|
|
1 y12 |
2 y22 |
m ym2 |
0, |
(5.29) |
|
|
|||||
|
|||||
1 y1n |
2 y2n |
m ymn |
0. |
|
|
В сокращенной и векторной формах условия (5.29) |
|||||
имеют соответственно вид: |
|
|
|
||
|
m |
|
|
|
|
|
i yik 0, (k 1,2,..., n) |
(5.30) |
|||
i |
1 |
|
|
|
|
|
1Y1 2Y2 |
mYm |
|
, |
|
где, Yk colon(yk1, yk 2 ,..., ykn ). |
|
|
|
||
Иными словами, система функций (5.28) является линейно независимой, если ни одна строка таблицы (5.28) не является при x (a,b) линейной комбинацией остальных строк этой таблицы. В противном случае системы (5.28) называются линейно зависимыми в (a,b).
В частности, две системы функций y11 , y11 ,..., y1n и y21, y22 ,..., y2n будут линейно независимыми в (a,b) , если не справедливо соотношение вида
175

y21 |
|
y22 |
|
y2n |
(a x b) . |
|
|
|
|
||
y11 |
|
y12 |
|
y1n |
|
Из (5.29) видно, что если одна из систем функций в (5.28) состоит из функций, тождественно равных нулю в интервале (a,b) , то эти системы функций линейно зависимы в (a,b) .
Пример. Система функций
|
y |
e3x |
, y |
|
e3x , |
y |
e3x ; |
|
11 |
|
12 |
|
13 |
|
|
|
y21 |
2e3x , y22 2e3x , y23 2e3x ; |
|||||
линейно зависимы в ( |
; |
) . |
|
|
|
||
Другая система функций |
|
|
|||||
y |
e 2x , |
y |
0, |
|
y |
e 2x ; |
|
11 |
|
12 |
|
|
13 |
|
|
y21 |
0, y22 |
e 2x , |
|
y23 |
e 2x ; |
|
|
является линейно независимой в |
; . |
|
|||||
Таким образом, если рассматривать элементы строки таблицы (5.28) как составляющие некоторого вектора в n - мерном пространстве (см. формулу (5.30) и ниже), то определение линейной независимости системы функций (5.28) является определением линейной независимости системы m векторов.
Рассмотрим необходимое условие линейной зависимости n систем функций*
y11, |
y12 , |
y1n; |
|
y21, |
y22, |
y2n ; |
|
|
|
|
(5.31) |
|
|||
yn1, |
yn2, |
|
ynn . |
Иными словами, рассматриваем необходимое условие
линейной зависимости системы |
n - мерных |
векторов |
Yk colon(yk1, yk 2 , , ykn ) (k |
1,2,..., n). |
|
Введем в рассмотрение |
определитель |
Вронского |
(вронскиан) для системы функций (5.31)
176

|
y11 |
y12 |
y1n |
|
|
|||
W (x) |
y21 |
y22 |
y2n |
. |
(5.32) |
|||
|
|
|
|
|||||
|
|
|
||||||
|
yn1 |
yn2 |
ynn |
|
|
|||
Теорема 4. Если |
n |
систем |
функций (5.31) |
линейно |
||||
зависимы в интервале (a,b) , то W (x) |
|
0 в (a,b) . |
|
|||||
Доказательство. Поскольку система функций (5.31) по условию линейно зависима, то по определению линейной зависимости имеем соотношение (5.29)
n |
|
|
|
|
i yik 0, (k 1,2,..., n; a x |
b), |
(5.33) |
||
i 1 |
|
|
|
|
где не все коэффициенты |
i |
равны |
нулю. |
Рассматривая |
|
|
|
|
|
систему равенств (5.33) как однородную линейную систему алгебраических уравнений относительно 1, 2 ,..., n , видим,
что она имеет ненулевое решение. Но из алгебры известно, что в этом случае определитель этой системы должен быть равным нулю. Определителем этой алгебраической системы уравнений является вронскиан (5.32). Так что W (x) должен
обращаться в нуль во всех точках интервала (a,b) .
Рассмотрим далее важное для теории линейных систем
необходимое и достаточное условие линейной независимости n решений однородной линейной системы n уравнений.
Пусть каждая из систем функций совокупности (5.31),
т.е. все Yk colon(yk1, yk 2 ,..., ykn ) (k 1,2,..., n) , является решением системы линейных однородных дифференциальных уравнений (5.23).
Теорема 5. Если n решений (5.31) однородной системы (5.23) линейно независимые в интервале (a,b) , в котором
определены и непрерывны коэффициенты aij (x) , то их
вронскиан W (x) не обращается в нуль ни в одной точке этого интервала.
177

|
Доказательство. |
Предположим |
обратное: |
пусть |
|||||||||||
W (x0 ) |
0 , |
где a |
x0 |
b . Составим систему алгебраических |
|||||||||||
уравнений |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ci ( yik )0 |
|
0, |
(k |
1,2,..., n), |
(5.34) |
|||
|
|
|
|
|
|
i |
1 |
|
|
|
|
|
|
|
|
где обозначено ( yik )0 |
yik (x0 ) . Определитель этой системы |
||||||||||||||
– есть W (x0 ) . По |
нашему |
предположению W (x0 ) 0 . |
|||||||||||||
Поэтому |
|
система |
(5.34) должна иметь |
ненулевое |
решение |
||||||||||
c |
c0 , |
c |
2 |
c0 ,..., c |
n |
c0 . Построим теперь функции |
|||||||||
1 |
1 |
|
|
2 |
|
n |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
y |
k |
(x) |
|
c0 y |
ik |
, |
(k |
1,2,..., n) . |
(5.35) |
||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
i |
1 |
|
|
|
|
|
|
Совокупность этих функций является решением системы дифференциальных уравнений (5.23), поскольку является линейной комбинацией решений (см. следствие теорем 1 и 2).
Поскольку все ci0 удовлетворяют алгебраической системе уравнений (5.34), то ясно, что решение (5.35) имеет нулевые начальные значения в точке x x0 :
y1 0, y2 0, ..., yn 0 при x x0 .
Но тогда решение (5.35) будет являться нулевым y1(x) 0, y2 (x) 0, ..., yn (x) 0
в силу единственности решения задачи Коши. Поэтому получается тождества
n |
|
|
|
|
c0 y |
ik |
(x) 0 (k 1,2,..., n), |
a x b, |
|
i |
|
|
|
|
i 1 |
|
|
|
|
где не все ci0 |
равны нулю. Это означает, что решения (5.31) |
|||
линейно зависимы в интервале (a,b) . |
Но это противоречит |
|||
условию теоремы. Следовательно, вронскиан не обращается в нуль ни в одной точке.
Таким образом, из доказанных теорем 4 и 5 следует: для того, чтобы n решений системы линейных однородных
178

уравнений (5.23) были линейно независимы в интервале (a,b) ,
необходимо и достаточно, чтобы их вронскиан не обращался в нуль ни в одной точке этого интервала.
Для установления линейной независимости n решений системы (5.23) достаточно убедиться в том, что W (x) отличен
от нуля хотя бы в одной точке (a,b) .
Введем понятие фундаментальной системы решений
линейной однородной системы n дифференциальных уравнений.
Совокупность n решений Yk (x) colon(yk1, yk 2 ,..., yk n) (k 1,2,..., n) однородной системы (5.23), определенных и линейно независимых в интервале (a,b) называется фундаме-
нтальной системой решений в этом интервале.
Из необходимого и достаточного условия линейной независимости n решений однородной линейной системы n дифференциальных уравнений, приведенного выше, следует:
система n решений будет фундаментальной системой решений в интервале (a,b) тогда и только тогда, когда определитель Вронского этих решений не равен нулю хотя бы в одной точке интервала (a,b) .
*Матрица вида
|
y11 |
y12 |
y1n |
|
||
Ф(x) |
y21 |
y22 |
y2n |
(5.36) |
||
|
|
|
|
|||
|
|
|||||
|
yn1 |
yn2 |
|
ynn |
|
|
столбцы которой сформированы из координатных функций
линейно независимых векторов Yk (x) (k |
1,2,..., n) - решений |
||
однородной |
системы, |
называется |
фундаментальной |
матрицей этой системы. Очевидно, что detФ(x) W(x).
Можно показать, что фундаментальная матрица (5.36) является решением матричного дифференциального уравнения
179
