
3447
.pdf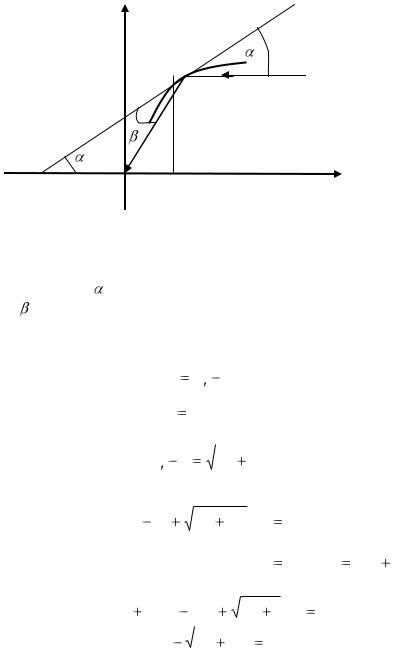
y |
|
|
|
M |
L |
|
|
y |
|
x |
|
0 |
P |
x |
Рис. 21
LM - луч света, падающий на кривую L и попадающий
после отражения в точку O ; |
TM - касательная к кривой в |
|||||||||
точке M ; |
- угол между лучом LM и касательной TM ; |
|||||||||
- угол между отраженным от зеркала лучом |
MO и |
|||||||||
касательной к зеркалу TM . |
|
|
|
|
||||||
Следовательно, |
TO |
|
y |
x. |
Подставляя |
найденные |
||||
|
|
|
||||||||
|
y |
|||||||||
|
|
|
|
|
|
|
|
|
||
величины в равенство TO OM , получаем дифференциальное |
||||||||||
уравнение – математическую модель задачи: |
|
|||||||||
|
|
y |
|
|
|
|
|
|
|
|
|
|
x |
x2 |
y 2 . |
|
|||||
|
|
|
|
|
||||||
|
|
y |
|
|||||||
|
|
|
|
|
|
|
|
|
||
Запишем это уравнение в симметрической форме:
ydx (x |
x2 y2 )dy |
0. |
(2.30) |
Легко видеть, что полученное уравнение является |
|||
однородным. Применив подстановку x |
uy (dx udy |
ydu), |
|
получаем уравнение с разделяющимися переменными:
y(udy ydu) |
y(u |
|
u 2 |
1)dy 0, |
|
|
|
|
|
|
|
ydu |
|
u 2 |
1dy |
0. |
|
30
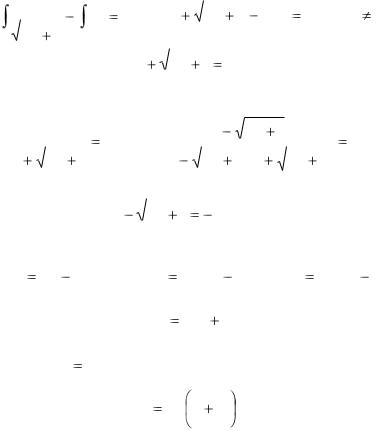
Разделяем переменные и интегрируем. Получим (см. таблицу интегралов):
|
du |
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
, ln |
u u 2 |
1 |
ln |
|
y |
|
ln |
|
C |
|
, C 0 ; |
|||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|||||||||||||||
|
u 2 1 |
|
y |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
u |
u 2 1 |
Cy . |
(2.31) |
|||||||||||
Для того чтобы разрешить последнее равенство относительно u , воспользуемся элементарным приемом:
|
|
1 |
|
|
|
|
1 |
, |
|
|
|
|
|
|
u |
|
|
|
|
u 2 |
1 |
|
1 |
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
u |
|
u 2 |
1 |
|
|
Cy |
(u |
|
u 2 |
|
|
1)(u |
|
u 2 |
1) Cy |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
. |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
u |
|
u2 |
1 |
|
|
|
|
|
|
|
|
|
|
(2.32) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cy |
|
|
|
|
|
|
|
|||||||
Складывая (2.31) и (2.32), находим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
2u |
Cy |
1 |
|
; |
|
2Cuy |
C 2 y2 |
1; |
|
2Cx |
C 2 y2 1; |
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
Cy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
y 2 |
2 |
x |
|
1 |
. |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
C 2 |
|
|
|
|
|
|
|
|||||
Обозначив |
1 |
|
|
|
p , получим окончательно уравнение линии: |
||||||||||||||||||||||||||||
C |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
y 2 |
2 p x |
|
p |
. |
|
|
|
|
|
|
(2.33) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, решением уравнения (2.30) служит парабола (2.33), ось симметрии которой – ось OX , а фокус лежит в начале координат. Ось искомой параболы параллельна пучку световых лучей, а фокус параболы лежит в оптическом фокусе.
Вращая эту параболу вокруг оси OX , найдем искомую зеркальную поверхность – параболоид вращения.
Очевидно, что если источник света поместить в фокусе параболы, то световые лучи после отражения пойдут параллельным пучком.
31
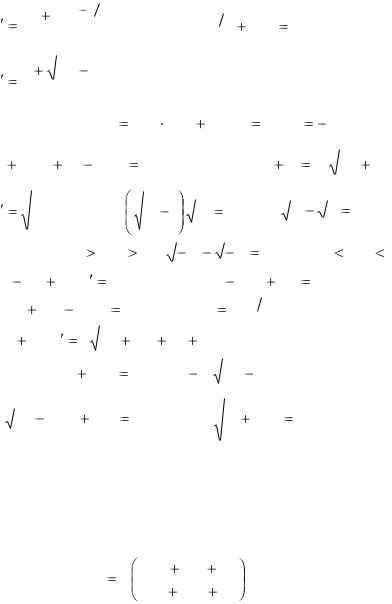
|
|
|
|
|
|
|
Задачи для самостоятельного решения |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
xy |
y 2e |
x y |
|
Ответ: e x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
1. |
y |
|
|
|
|
|
. |
|
ln |
x |
|
|
|
c . |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
x2 |
|
y 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2. |
y |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: arcsin |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x . |
|
|
|||||||||||||||||
|
|
sigx ln |
x |
|
|
|
|
C, |
|
|
y |
|
|
x, |
|
y |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
3. |
(x |
y)dx |
|
( y |
x)dy |
0. |
|
Ответ: arctg |
|
|
C |
ln |
x2 |
y 2 . |
|||||||||||||||||||||||||||||||||||||||
|
x |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
y |
|
|
|
y |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
4. |
|
|
|
. |
|
|
Ответ: |
|
1 |
|
|
|
|
x |
|
|
|
C, |
или |
|
y |
|
x |
C, |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
если x |
0, y |
0 ; |
|
|
|
|
y |
|
|
|
|
|
|
|
x |
|
|
C, |
если x |
0, y |
0 . |
|||||||||||||||||||||||||||
5. |
x2 |
|
y2 |
|
2xyy |
0. |
|
Ответ: |
|
x2 |
|
2Cx |
y2 |
0. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
6. |
y2dx |
x(x |
y)dy 0. Ответ: |
|
y |
Ce y x . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
7. |
(x2 |
|
xy) y |
x x2 |
y 2 |
xy y 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
y |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
Ответ: C |
|
ln |
|
x |
|
arcsin |
|
|
|
|
x2 |
y2 . |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x |
|
x |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
ln |
|
y |
|
C. |
|
|
|
|
|
|
|||||||||
8. |
(2 |
xy |
|
|
x)dy |
|
ydx |
0. |
|
|
Ответ: |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
y |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2.3. Дифференциальные уравнения первого порядка, приводящие к однородному
Интегрируемыми в квадратурах будут приводящиеся к однородным (либо непосредственно к уравнениям с разделяющимися переменными) уравнения вида:
dy |
f |
a1x |
b1 y |
c1 |
|
|
|
|
|
|
. |
(2.34) |
|
dx |
a2 x |
b2 y |
c2 |
|||
1. Уравнение (2.34) будет являться уравнением с разделяющимися переменными в следующих случаях:
32
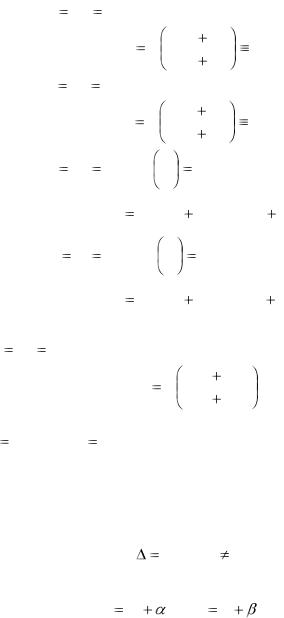
1)a1 a2
2)b1 b2
3)a1 b2
4)a2 b1
0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
dy |
|
|
|
|
|
b1y |
c1 |
|
|
|
~ |
||||
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
f1( y); |
||
|
dx |
|
|
b2 y |
c2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||
0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dy |
|
|
|
|
|
a1x |
c1 |
|
|
|
~ |
||||
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
f2 (x); |
||
|
dx |
|
|
a2 x c2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||
0 и f |
|
u |
f (u) f |
|
|
(v) , |
||||||||||
|
|
|
|
|
|
2 |
||||||||||
|
|
|
|
|
v |
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
dy |
f1 |
(b1 y c1) f2 (a2 x c2 ); |
||||||||||||||
|
|
|
||||||||||||||
dx |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 и f |
|
u |
f (u) f |
|
|
(v) , |
||||||||||
|
|
|
|
|
2 |
|||||||||||
|
|
|
|
|
|
v |
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
dy |
|
f1(a1x c1) f2 (b2 y c2 ) . |
|
||||||
|
|
|
|
|
|
|
||||||
|
|
|
dx |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
2. |
Уравнение |
(2.34) |
будет |
являться однородным, |
если |
||||||
c1 |
c2 |
0 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
f |
a1x |
b1 y |
|
||
|
|
|
|
|
|
|
|
|
|
. |
(2.35) |
|
|
|
|
|
|
|
dx |
a2 x |
b2 y |
||||
|
Обратившись к результатам п.2.2 видим, что подстановка |
|||||||||||
y |
ux |
(или x uy) |
|
приводит уравнение (2.35) к уравнению с |
||||||||
разделяющимися переменными. |
|
|
|
|||||||||
3.Рассмотрим общий случай приведения уравнения (2.34)
коднородному уравнению. Пусть хотя бы одно из чисел c1, c2
отлично от нуля и не равен нулю определитель
|
a1 |
b1 |
|
0 . |
(2.36) |
|
a2 |
b2 |
|
||
|
|
|
|
||
Выполним линейную замену обеих переменных |
|
||||
x X |
, |
y Y |
. |
(2.37) |
|
Тогда уравнение (2.34) примет вид:
33
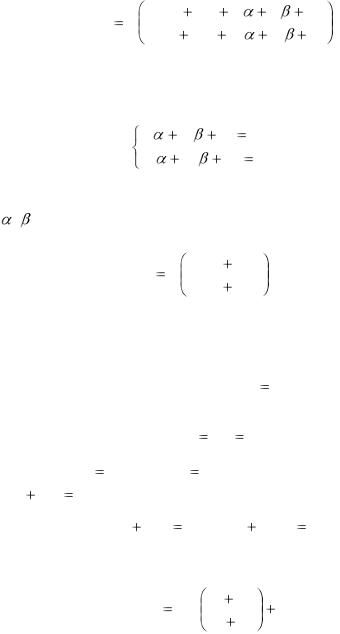
dY |
|
a1X b1Y a1 |
b1 |
c1 |
(2.38) |
|
|
f |
|
|
|
. |
|
dX |
a2 X b2Y a2 |
b2 |
c2 |
|||
Чтобы преобразовать уравнение (2.38) в однородное потребуем, чтобы свободные члены в числителе и знаменателе аргумента функции, стоящей в правой части уравнения,
обращались в нуль: |
|
|
|
|
|
a1 |
b1 |
c1 |
0, |
(2.39) |
|
a2 |
b2 |
c2 |
0. |
||
|
Неоднородная система линейных уравнений (2.39), при условии (2.36), однозначно определяет неизвестные параметры
, . Таким образом, |
в новых переменных X , Y получаем |
|||||||
однородное дифференциальное уравнение 1-го порядка: |
||||||||
|
dY |
|
a1X |
b1Y |
|
(2.40) |
||
|
|
|
f |
|
|
. |
|
|
|
dX |
a2 X |
b2Y |
|
||||
Интегрируя |
уравнение |
(2.40) |
и |
возвращаясь к |
||||
переменным x, y |
по |
формулам (2.37), |
получим общий |
|||||
интеграл уравнения (2.34).
4. Остановимся теперь на случае, когда условие (2.36) не выполняется. Если определитель 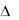 0 , элементы его строк пропорциональны:
0 , элементы его строк пропорциональны:
|
|
|
|
|
|
|
|
a1 |
|
|
b1 |
k, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
b2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
поэтому |
a1 |
ka2 , |
|
|
b1 kb2 . |
Применяя |
подстановку |
|||||||||||
a1x b1 y |
z , получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
a |
|
x b y kz, |
|
a b |
dy |
|
dz |
. |
||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
2 |
|
2 |
|
|
|
|
|
1 1 dx |
|
dx |
|
||||
Таким |
образом, |
|
|
|
приходим |
к |
уравнению с |
|||||||||||
разделяющимися переменными: |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
dz |
|
b1 f |
|
z |
c1 |
|
a1 . |
|
|
|
|||
|
|
|
|
|
dx |
kz |
c2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
34 |
|
|
|
|
|
|
|
|

5. Имеется еще один тип дифференциального уравнения 1-го порядка, приводимое к уравнению с разделяющимися переменными – обобщенное однородное уравнение. Это уравнение вида
P(x, y)dx Q(x, y)dy 0 ,
где коэффициентные функции удовлетворяют условиям:
P(tx, t k y) |
t m P(x, y), |
Q(tx, t k y) |
t m k 1Q(x, y). |
Не останавливаясь на методе интегрирования таких уравнений, отсылаем читателей к пособию (А.М. Самойленко
[7]).
|
|
|
|
|
y |
1 |
2 |
|
|
Пример. |
Решить уравнение y 2 |
|
. |
|
|||||
|
|
|
|
||||||
x |
y |
2 |
|
||||||
Решение. |
Выполним |
замену |
переменных |
|
x X |
, |
|||
y Y |
. Для нахождения |
и |
получаем систему |
|
|||||
1 02 .
Получаем X x 3, Y y 1. Уравнение для новых
переменных является однородным дифференциальным уравнением вида
|
|
|
|
|
|
|
|
dY |
|
2 |
|
Y 2 |
|
|
. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
dX |
( X Y )2 |
|
|
|
|
|
||||||||||
Положим Y |
uX , тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
X |
du |
|
u |
|
2u 2 |
|
, |
|
X |
du |
|
|
|
u |
u 2 |
0. |
|||||||
dX |
(1 |
u)2 |
|
|
dX |
(1 |
u)2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Отсюда получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
ln |
u |
|
|
|
2arctgu |
ln |
X |
|
ln |
C |
, |
|
||||||||
|
|
|
|
uX |
C exp( |
2arctgu). |
|
|
|||||||||||||||
Возвращаясь к переменным x, y , имеем:
35

y |
1 C exp 2arctg |
y |
1 |
, |
||||
x |
3 |
|||||||
|
|
|
|
|
||||
или |
|
|
|
|
|
|
|
|
( y |
1) exp 2arctg |
y |
1 |
C. |
||||
x |
3 |
|
||||||
|
|
|
|
|
||||
2.4.Линейное уравнение
1.Введем понятие линейного дифференциального уравнения 1-го порядка.
Уравнение вида
y p(x) y q(x) |
(2.41) |
|
называется линейным. Оно содержит искомую функцию y |
и ее |
|
производную y в первой степени. |
Если разрешить |
это |
уравнение относительно производной, то получим уравнение
y |
p(x) y q(x). |
|
|
|
Полученное уравнение является уравнением вида (2.1), в |
||||
котором функция f (x, y) |
линейна по y , с коэффициентами, |
|||
вообще говоря, зависящими от x . |
В частном случае |
p и q |
||
могут быть постоянными величинами. |
|
|
||
Всюду далее будем предполагать, что функции |
p(x) и |
|||
q(x) непрерывны во всем интервале (a,b) ( a |
, b |
). |
||
Если в уравнении |
(2.41) функция q(x) тождественно |
|||
равна нулю при всех x (a,b) , то уравнение примет вид |
|
|||
y |
p(x) y |
0 |
|
(2.42) |
и называется однородным. Его левая часть является
однородной линейной функцией от y |
и y . Уравнение (2.41), в |
||
котором q(x) 0 |
называется |
неоднородным |
линейным |
уравнением. |
|
|
|
Более общее уравнение |
|
|
|
|
p0 (x) y p1(x) y |
q(x) , |
(2.43) |
36
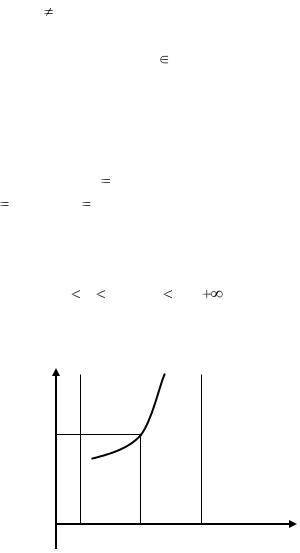
в котором p0 (x) 1, также называется линейным. Если p0 (x) , p1(x) , q(x) непрерывны в интервале (a,b) , причем p0 (x) не обращается в нуль при всех x (a,b) , то уравнение (2.43), делением обеих частей на p0 (x) , приводится к виду (2.41).
2*. Из сформулированной в §1 теоремы Пикара о достаточном условии существования и единственности решения задачи Коши, вытекает, что в предположении
непрерывности функций |
p(x) и |
q(x) |
уравнение (2.41) имеет |
||||
единственное решение |
y |
y(x) , |
удовлетворяющее начальному |
||||
условию y |
y0 при x |
x0 , |
где в качестве |
x0 можно брать |
|||
любое число |
из интервала |
(a,b) , а |
y0 |
можно выбирать |
|||
произвольно.
Это означает, что через любую точку M 0 (x0, y0 ) полосы a x b, 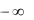 y
y  ,
,
проходит одна и только одна интегральная кривая уравнения
(2.41).
y
y0 |
M 0 |
0 |
a |
x0 |
b |
x |
Рис.6 Полоса единственности решения линейного уравнения
Отсюда следует, что вся указанная полоса на плоскости XOY заполнена непересекающимися гладкими интегральными
37

кривыми линейного уравнения. При этом каждая интегральная кривая определена во всем интервале (a,b) и представляет собой график частного решения (рис. 6). Интегральные кривые
однородного уравнения (2.42) не могут пересекать ось OX .
Действительно, поскольку y 0 (a x b) является решением
уравнения (2.42), то пересечение интегральной кривой оси OX означало бы нарушение единственности решения уравнения (через точку пересечения проходили бы две интегральные кривые).
3. Рассмотрим построения общего решения однородного уравнения, соответствующего неоднородному линейному уравнению. Записав уравнение (2.42) в симметрическом виде
dy p(x) ydx 0 ,
получаем уравнение с разделяющимися переменными. Разделяя переменные и интегрируя, имеем:
y |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
p(x)dx, |
ln |
|
y |
|
ln |
|
C |
|
p(x)dx, |
(C 0), |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||
|
y |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
y |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
y |
Ce |
p( x)dx , (C |
0), |
|
|
|
|
|
|||||
y |
C exp |
p(x)dx , |
|
|
|
|
C |
. |
(2.44) |
||||
В формуле (2.44) содержатся все решения однородного уравнения (2.42). Заменим в формуле (2.44) неопределенный интеграл определенным интегралом с фиксированным нижним
пределом |
x0 |
(a, b) |
и |
переменным |
верхним пределом |
x (a,b) , |
где |
(a,b) |
- интервал, в котором функция p(x) |
||
непрерывна. Получим |
|
|
|
||
|
|
|
|
x |
|
|
|
y |
C exp |
p(x)dx . |
(2.45) |
|
|
|
|
x0 |
|
38

Обозначим y(x0 ) y0 |
и положим в этой формуле x |
x0 . |
|
Тогда получим C |
y0 . Подставив это значение C в формулу |
||
(2.45), получим: |
|
|
|
|
|
x |
|
y |
y0 exp |
p(x)dx . |
(2.46) |
|
|
x0 |
|
Если y0 - произвольно, то формула (2.46) является общим решением линейного однородного уравнения (2.42) в форме Коши. Если же y0 - фиксировано, то (2.46) представляет собой
решение уравнения (2.42) с начальными данными x0 , y0 .
Из формулы общего решения (2.46) однородного
уравнения видно, |
что если |
y0 |
0 , |
|
то решение не обращается |
||||||||||||||||||||||||||
в нуль ни в одной точке. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Пример. |
|
Найти общее решение уравнения |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
x |
y 0. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
1 |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение. |
|
|
В этом |
случае |
p(x) |
|
|
|
|
|
x |
|
|
- |
функция |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
1 x2 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
непрерывная в |
интервале |
( |
1,1) . |
Воспользуемся |
|
формулой |
|||||||||||||||||||||||||
(2.44), предварительно вычислив |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
x |
|
|
|
|
t |
1 |
x2 |
|
|
1 |
|
dt |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 x2 ; |
|||||||||||||||||||
p(x)dx |
|
|
|
|
dx |
|
|
|
t |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
2 |
dt |
|
|
|
2xdx |
|
|
|
|
t |
|
|
||||||||||||||||
1 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
y |
Ce 1 |
x 2 , |
|
|
|
|
C |
. |
|
|
|
|
|
|
|||||||||||||
Полученная формула дает общее решение уравнения в области:
1 x 1, |
y |
. |
Пример. Найти решение задачи Коши для линейного однородного уравнения:
39
