
3447
.pdf
Подставляя в исходную систему уравнений и приравнивая коэффициенты при соответствующих степенях x , получим однородную систему уравнений для определения 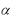 с рангом r 2
с рангом r 2
|
|
|
|
|
(1) |
(2) |
|
|
(1) |
0 |
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
(2) |
|
|
(2) |
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
(1) |
(1) |
|
|
(2) |
0 |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
(2) |
|
|
(2) |
0. |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Следовательно, из искомых постоянных две произвольны, |
|||||||||||||||
например, |
(2) |
C2 |
(1) |
C1, поэтому из этой системы для |
||||||||||||
2 |
1 |
|||||||||||||||
остальных |
(2) , |
(1) |
будет |
(1) |
C |
|
|
C |
2 |
. |
Отсюда общее |
|||||
|
|
|
1 |
2 |
|
2 |
|
|
1 |
|
|
|
|
|
||
решение исходной системы будет |
|
|
(2) |
C2 . |
|
|
|
|||||||||
|
|
1 |
|
|
|
|||||||||||
|
|
|
|
y |
C e x C |
2 |
xex |
|
|
|
|
|
|
|
||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z ( C C |
2 |
)e x |
C |
2 |
xex . |
|
|
|||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
|
3. Если среди корней характеристического уравнения |
|||||||||||||||
(5.62) |
|
есть |
комплексное |
|
спряженные |
пары |
||||||||||
m |
|
m |
i m , |
m 1 |
m |
i |
m , то |
|
этим |
корням |
будут |
|||||
соответствовать частные решения |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
y(1) |
(1) e( m i |
m) , |
|
|
y(2) |
|
|
(2) |
|
e( m i m) , |
|
||
|
|
|
m |
m |
|
|
|
|
m |
|
|
m |
|
|
|
|
причем |
(i) определяются из систем (5.62). Можно показать, |
|||||||||||||||
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
что |
действительные и |
мнимые |
|
части |
|
|
|
|
|
также являются |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
( i ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x m |
|
|
|
|
|
решениями системы (5.56). Таким образом, можно записать два частных решения:
ym(1) e ym(2) e
m |
(1) |
m x |
(2) |
m x |
||
|
|
m cos |
|
m sin |
||
m |
|
|
|
|
(2) |
m x , |
m cos |
m x |
|
||||
|
|
m sin |
||||
200

где |
(1) |
, |
(2) |
, |
|
(1) |
, |
|
(2) |
- |
действительные |
|
|
||||||||||
m |
m |
|
m |
|
m |
||||||
коэффициенты, |
связанные с |
m(1) , |
m(2) . |
|
|||||||
Следовательно, можно составить фундаментальную систему решений только из действительных решений.
Пример 3. Дана система дифференциальных уравнений
dy1 |
|
7 y1 |
y2 |
dx |
|
||
|
|
|
|
dy2 |
|
2 y1 |
5 y2 . |
dx |
|
||
|
|
|
Найдем ее общее решение.
Решение. Характеристическое уравнение для этой системы имеет вид
|
|
7 |
1 |
|
|
0 |
или |
|
2 |
12 |
37 0, |
||
|
|
2 |
5 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
корни этого уравнения |
1 |
6 |
i, |
|
2 |
|
6 |
i. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Подставляя эти корни в (5.62), получим |
|
|||||||||||
|
|
|
|
(1) |
1, |
|
(1) |
1 |
i. |
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
Соответствующее частное решение yij (x) |
будет |
||||||||||||
|
|
y(1) |
e( |
6 |
i)x ; |
y |
(1) |
(1 |
i)e( |
6 |
i)x . |
||
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
Для |
2 |
6 i , получим соответственно |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
1, |
|
|
(2) |
1 |
i; |
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
y(2) |
e( |
6 |
i) x ; |
y |
(2) |
(1 |
i)e( |
6 |
i) x . |
||
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
Поскольку из четырех получившихся функций в общее решение для 1, 2 должны войти лишь два линейно независимых решения с произвольными постоянными C1, C2 , преобразуем получившиеся решения следующим образом
201

y1(1) y2(1) y1(1) y2(1)
для y1(2) , y1(2) y2(2)
e 6x (cosx |
i sin x); |
|
|
(1 i)e 6x (cosx i sin x); или |
|
||
e 6x cos x |
ie 6x sin x; |
|
|
e 6x (cosx |
sin x) |
ie 6x (cosx |
sin x); |
y2(2) будет |
|
|
|
e 6x cos x |
ie 6x sin x), |
|
|
e 6x (cosx |
sin x) |
ie 6x (cosx |
sin x). |
Поэтому составляя общее решение из действительных и мнимых частей этих решений для yij (x).найдем
y |
|
C e 6x cos x |
C |
2 |
e 6x sin x. |
||
1 |
1 |
|
|
|
|
||
y |
2 |
C e 6x (cos x |
sin x) C |
2 |
e 6x (cos x sin x). |
||
|
1 |
|
|
|
|
||
Известно, что линейное однородное дифференциальное уравнение n-го порядка
|
d n y |
a |
|
(x) |
d n 1 y |
a |
|
|
(x) |
d n 2 y |
... a (x) |
dy |
a |
|
y (5.64) |
||||
|
|
n 1 |
|
|
|
|
n |
2 |
|
|
|
0 |
|||||||
|
dxn |
|
|
dxn 1 |
|
|
dxn 2 |
1 |
dx |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
эквивалентно линейной, |
однородной системе |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
dy0 |
|
y1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
dy1 |
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
(5.65) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
dyn 1 |
a0 y0 a1 y1 ... |
an 1 yn 1. |
|
|
|
||||||||
|
|
|
|
|
|
dx |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Будем считать все ak |
|
const. |
|
|
|
|
|
||||||||||||
|
|
Характеристическая матрица для (5.65) в этом случае |
|||||||||||||||||
будет иметь вид |
|
|
|
|
|
|
|
|
|
|
|
||||||||
202

1 |
0 |
|
0 |
0 |
1 |
|
0 |
|
|
|
|
a0 |
a1 |
|
an 1 |
или
det( ) |
n |
n |
1 |
... a1 |
a0 |
0 . |
|
an 1 |
|
||||
Если же вычеркнуть из матрицы первый столбец и |
||||||
последнюю строку, получим определитель равный |
+I или –I. |
|||||
Следовательно, характеристический многочлен, если имеет
корень k |
кратности |
S k , |
то матрица имеет элементарный |
||||||
делитель |
( |
|
k )Sk . |
Поэтому |
корню |
k |
будут |
||
соответствовать S k линейно независимых решений вида |
|
||||||||
|
(C |
0 |
C x |
... |
C |
Sk 1 |
x Sk 1 )e k x . |
|
(5.66) |
|
|
1 |
|
|
|
|
|
||
Таким образом, методы решения систем типа (5.57) могут быть использованы для решения линейных дифференциальных уравнений n-го порядка, разрешенных относительно производных.
Пример 4. Найти общее решение дифференциального уравнения
|
|
y 3y 3y |
y |
0, |
|
||||
Обозначим y y0 , y y0 |
y1, |
y |
y1 y2 , y |
y2 . |
|||||
Тогда |
|
|
|
|
|
|
|||
|
dy0 |
|
y1 |
, |
|
|
|
||
|
|
dx |
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
dy1 |
|
|
y2 |
, |
|
|
(5.67) |
|
|
|
dx |
|
|
|
||||
|
|
|
|
|
|
|
|
||
|
dy2 |
|
y0 |
3y1 |
3y2 . |
|
|||
|
|
dx |
|
|
|||||
|
|
|
|
|
|
|
|
||
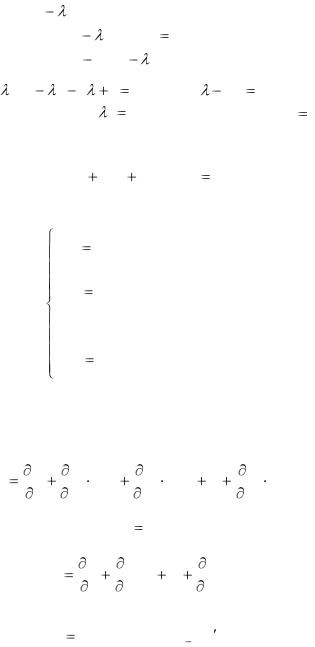
Характеристическое уравнение системы (3.12) имеет вид
203
|
|
|
1 |
|
0 |
|
|
|
|
|
0 |
|
|
1 |
|
0, |
т.е |
|
|
1 |
3 |
|
3 |
|
|
|
2 (3 |
) |
3 |
1 |
0 |
или ( |
1)3 0 . |
||
Поскольку |
корень |
1 |
1 |
имеет |
кратность S 3 , то, |
|||
учитывая (5.66), получим общее решение (5.67), а следовательно, и исходного уравнения третьего порядка в виде
(C0 C1x C2 x2 )ex
Для нахождения общего решения дифференциальных уравнений вида
|
dy1 |
|
|
f1 |
(x, y1, ..., yn ), |
||
|
dx |
|
|
||||
|
|
|
|
|
|
|
|
|
dy2 |
|
|
f 2 |
(x, y1 |
, ..., yn ), |
|
|
dx |
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||
|
dyn |
|
|
fn (x, y1 |
, ..., yn ) |
||
|
dx |
|
|
||||
|
|
|
|
|
|
|
|
y(x).
нормальных систем
(5.68)
применяется также метод последовательного исключения неизвестных функций, то есть сведение системы (5.68) к уравнению вида (5.64). Для этого, дифференцируя первое уравнение из (5.68) по x , получим
|
d 2 y |
|
|
f |
1 |
|
f |
1 |
|
dy |
|
|
f |
1 |
|
dy |
2 |
|
|
|
|
f |
1 |
|
dy |
n |
|
|||||
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
... |
|
|
|
|
. |
|||||||||||
|
dx2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
x |
y1 |
|
|
dx |
|
|
y2 |
dx |
|
|
|
|
yn |
|
dx |
||||||||||||||
Используя тот факт, что |
|
dyk |
|
|
|
f k , |
|
найдем |
|
|
|
|
|
|||||||||||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
d |
2 y |
|
|
|
f |
|
|
|
f |
1 |
|
|
|
|
|
|
f |
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
f1 |
... |
|
|
|
fn . |
|
|
|
(5.69) |
|||||||||
|
|
|
|
dx2 |
|
|
|
x |
|
|
|
y1 |
|
|
yn |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Определим xn из первого уравнения системы (5.68) yn g(x, y1, y2 ,..., yn 1, y1 )
204
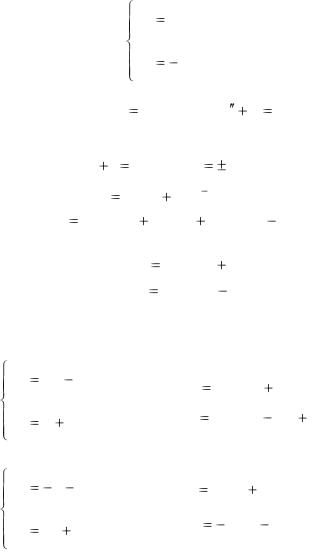
Подставим yn в (5.69) и, таким образом, исключим эту неизвестную функцию из (5.69). Продолжая эту процедуру,
можно получить |
|
уравнение n-го |
порядка для одной |
||||||
неизвестной функции. |
|
|
|
||||||
Пример 5. |
Найти |
общее решение |
|||||||
|
|
|
|
dy |
|
z, |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
dz |
|
y. |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|||
|
|
|
|
|
|
|
|||
Решение. |
d 2 y |
|
|
dz |
, |
т.е. y |
y 0 . |
||
dx |
2 |
|
|
dx |
|||||
|
|
|
|
|
|
||||
Характеристическое уравнение имеет вид
|
|
|
k 2 |
1 0; |
|
|
|
|
k |
|
|
i, |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
y(x) |
C eix |
|
|
|
C |
2 |
e ix |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
y(x) C1(cosx i sin x) C2 (cosx |
|
|
i sin x), тогда общее |
|||||||||||||||||||
решение можно записать |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
y(x) |
|
C1 cos x |
C2 sin x, |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
z(x) |
C2 cos x |
C1 sin x. |
|
|
|
|
|
||||||||||||||
|
|
|
Задачи для самостоятельного решения |
||||||||||||||||||||||
|
|
|
Решить системы уравнений: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
dy |
|
4 y z, |
|
|
|
|
|
|
y e3x (C C |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
x), |
|
||||||||||||||
|
dx |
|
|
|
|
|
|
2 |
|
||||||||||||||||
1. |
|
|
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
dz |
|
|
|
|
|
|
|
|
|
3x |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
y 2z. |
|
|
|
|
|
|
z e |
(C1 |
|
C2 |
|
C2 x). |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
y 2z, |
|
|
|
|
|
|
y C e x |
C |
|
|
e2x , |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
2. |
|
|
Ответ: |
|
|
|
|
|
|
|
|
|
3C2 |
|
|
|
|||||||||
dz |
|
|
|
|
|
|
|
|
|
x |
|
|
2 x |
|
|||||||||||
|
|
3y 4z. |
|
|
|
|
|
|
|
z |
C1e |
|
e |
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
205

|
|
dy |
2 y |
z, |
|
|
|
|
|
|
e2x (C cos x |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
y |
C |
|
sin x), |
|||||||||||||||||
|
|
dx |
|
|
|
|
|
2 |
|||||||||||||||||||||
3. |
|
|
|
|
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
|
dz |
|
|
|
|
|
|
|
|
|
2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
y |
|
2z. |
|
|
|
|
|
z |
e |
(C1 sin x |
C2 cos x). |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
dx |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dy |
y |
2z, |
|
y |
|
C1 cos x |
|
|
|
C2 sin x, |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
4. |
|
|
|
Ответ: z |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
dz |
|
|
|
|
(C |
|
|
|
C |
|
|
) cos x |
(C |
C |
|
) sin x . |
|||||||||||||
|
|
|
|
|
|
|
|
|
2 |
2 |
|||||||||||||||||||
|
|
|
|
y |
z. |
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
dy |
z, |
|
|
|
|
|
|
|
C e x |
|
|
|
|
|
|
|
x , |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
y |
|
|
|
|
C |
|
e |
|
|
|
|
|
|||||||||
|
dx |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||
5. |
|
|
|
Ответ: |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
dz |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||||
|
y. |
|
|
|
|
z |
|
|
C1e |
|
|
C2e |
. |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
dy |
y |
2z. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
y |
|
2C1 cos x |
|
|
|
2C2 sin x, |
|
|
|
|
||||||||||||||
6. |
dx |
Ответ: |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
dz |
|
|
|
|
z |
|
(C1 |
|
|
C2 ) cos x |
|
(C1 |
|
C2 ) sin x. |
|||||||||||||||
|
y |
z. |
|
|
|
|
|
|
|||||||||||||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
dy |
|
|
y z, |
|
|
|
|
|
|
|
|
|
|
|
|
e2x |
|
1 |
x 2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
y C C |
|
|
|
x , |
|
|
|||||||||||||||
|
dx |
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||
7. |
|
|
|
Ответ: |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
||||||
dz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x y z. |
|
|
z C |
|
e2x |
|
|
|
C |
|
1 |
x 2 |
|
x 1. |
|||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
4 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
dy |
2 y |
z |
sin x, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
8. |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
dz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
4 y |
|
2z |
cos x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Ответ: |
|
y C1 |
|
|
C2 x 2 sin x, |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
z |
|
2C1 |
|
|
C2 (2x |
|
1) 3sin x 2 cos x. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
206

6. ФУНКЦИОНАЛЬНЫЕ РЯДЫ И ИХ ПРИЛОЖЕНИЯ К РЕШЕНИЮ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
6.1. Функциональные ряды. Сходимость и равномерная сходимость
Функциональными рядами называются такие ряды,
членами которых являются функции.
Разложение функций в ряды, членами которых являются функции более простые, чем исходные, используется при вычислении значений функций и при их исследовании, при интегрировании функций и при решении дифференциальных уравнений. Однако, при проведении операций с функциональными рядами, таких как дифференцирование или интегрирование, сходимости ряда в обычном смысле (поточечной) недостаточно. Поэтому в математике вводят и другие виды сходимости ряда.
Пусть дан функциональный ряд
uk (x) u1 (x) u2 (x) ... uk (x) ... , |
(6.1) |
k 1
где все функции заданы, например, на сегменте [a,b] .
Определение. |
Функции |
|
S1(x) |
u1(x) , |
||
S1(x) u1(x) |
u2 (x) ,…, Sn (x) |
u1 (x) ... |
un (x), называются |
|||
частичными |
суммами |
функционального |
ряда |
(6.1). |
||
Последовательность функций |
(Sn (x))1 |
S1(x), S2 (x), …, |
||||
Sn (x),... называется последовательностью частичных сумм
функционального ряда.
Введем понятие предела последовательности функций.
Определение. Последовательность функций
f1 (x), f2 (x), ..., |
fn (x),...( fn (x))1 |
называется |
сходящейся к |
функции f (x) |
на сегменте |
[a,b] , если |
при каждом |
фиксированном |
x из [a,b] последовательность чисел fn (x) |
||
сходится к числу f (x) , т.е. если для любого 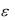 0 и каждого
0 и каждого
207
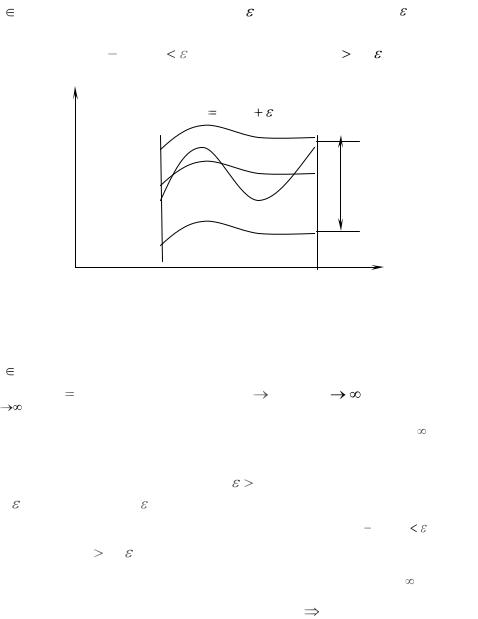
x [a,b] найдется такое число |
N( |
, x) , зависящее от |
и, |
||
вообще говоря, от x , что будет |
|
|
|
||
|
fn (x) f (x) |
|
при |
котором n N ( , x). |
|
|
|
|
|||
|
y |
|
|
|
|
|
|
y |
f (x) |
|
|
y  fn (x)
fn (x)
y 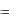 f (x)
f (x)
y 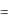 f (x)
f (x) 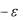
2 ε
x
|
|
Рис. 12 |
|
Такую |
сходимость |
последовательности |
функций |
называют |
'' поточечной '' сходимостью – для каждой точки |
||
x [a,b] N |
зависит от |
x . Этот факт |
обозначают |
lim fn (x) f (x) на |
[a,b] , или fn (x) |
f (x), |
n |
. |
|
|||
x |
|
|
|
|
|
|
|
|
Определение. |
Последовательность функций |
( fn (x))1 |
||||||
называется равномерно сходящейся к функции |
f (x) на |
|||||||
сегменте [a,b] , |
если для любого |
0 найдется такое число |
||||||
N( ) , зависящее от |
и не зависящее от x , |
что отклонение |
||||||
fn (x) от f (x) |
удовлетворяет |
неравенству |
|
fn (x) |
f (x) |
|
||
|
|
|||||||
при каждом n |
N( |
) и сразу для всех x |
из [a,b] . |
|
|
|||
Равномерная сходимость последовательности ( fn (x))1 к |
||||||||
функции f (x) обозначается символом |
fn (x) |
|
f (x) |
на [a,b] . |
||||
Приведенный рис. 12 иллюстрирует равномерную сходимость последовательности к предельной функции f (x) : графики всех
208

функций fn (x) |
при n |
N( |
) |
лежат |
в |
“ |
полоске”, |
||||||||||||||||||||||||||||
окружающей график функции f (x) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
Пример. Последовательность функций с общим членом |
|||||||||||||||||||||||||||||||||
|
fn (x) |
|
1 |
sin nx |
|
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Решение. |
Действительно, |
|
1 |
sin nx |
0 |
|
|
|
sin nx |
|
1 |
|
|||||||||||||||||||||
|
|
|
n |
|
|
|
n |
|
|
|
|
|
|
n |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
сразу для всех x , |
|
|
x |
|
, если только n |
|
N ( |
) |
1 |
. |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
Пример. |
Последовательность функций |
(xn ) |
|
|
|
сходится |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
на |
сегменте |
[0,1] |
к |
функции |
f (x) : f (x) |
|
0 |
при |
0 |
|
x |
1, |
|||||||||||||||||||||||
|
f (x) 1 при x |
1. Эта сходимость будет |
неравномерной. |
||||||||||||||||||||||||||||||||
Действительно, |
|
|
пусть |
|
|
|
0 |
|
1, |
0 |
|
x |
1. |
|
|
|
|
|
Тогда |
||||||||||||||||
|
fn (x) |
|
|
f (x) |
|
|
xn |
|
|
|
выполняется |
|
|
|
только |
|
|
для |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
n |
N ( |
, x) |
ln |
. |
Но |
|
N( |
, x) |
|
|
|
при |
x |
|
1 |
0, |
0 |
|
|
|
1. |
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Следовательно, |
|
при |
0 |
|
1 |
нет |
такого |
конечного |
числа |
||||||||||||||||||||||||||
|
N( ) , не зависящего от |
|
x , чтобы |
|
fn (x) |
|
|
f (x) |
|
xn |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
выполнялось при каждом n |
N( |
) |
сразу для всех x из [0,1) . |
||||||||||||||||||||||||||||||||
|
|
Но если сегмент [0,1] заменить меньшим [0,1 |
] , |
где |
|||||||||||||||||||||||||||||||
0 |
|
1, то |
на |
этом |
сегменте |
xn |
0 . |
|
Действительно, |
||||||||||||||||||||||||||
|
N ( |
, x) |
|
|
ln |
|
|
N ( |
) |
|
ln |
|
|
при |
0 |
x |
|
1 |
, |
|
|
|
поэтому |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
ln x |
|
|
|
ln(1 |
|
) |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
fn (x) |
|
f (x) |
|
|
xn |
|
при n |
N ( ) |
|
|
ln |
|
|
сразу для всех x |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
ln(1 |
) |
|
|||||||||||||||||||||||||||
из |
[0, 1 |
]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Определение. Функциональный ряд (6.1) называется сходящимся, если сходится последовательность его частичных сумм
209
