
3447
.pdf
Доказательство. По условию теоремы фундаментальная система решений однородной системы известна; т.е. известны функции
|
z11 (x), |
z12 (x), z1n (x), |
|
|
||
|
z21 (x), |
z22 (x), z2n (x), |
|
|
||
|
|
|
|
|
|
|
|
zn1 (x), |
zn2 (x), znn (x). |
|
|
||
|
|
|
|
n |
|
|
Решение неоднородной системы yk |
ak i(x) yi (x) |
fk (x) |
||||
|
|
|
|
i 1 |
|
|
(k 1,2,..., n) будем искать в виде |
|
|
|
|
||
yk |
Ci (x)zik (x) f k (x) (k |
1,2,..., n) , |
(5.51) |
|||
i |
1 |
|
|
|
|
|
где Ci (x) (i 1,2,..., n) - некоторые непрерывно дифференцируемые функции.
Отметим, что при постоянных Ci формула (5.51) дает
общее решение однородной системы.
Подставим (5.51) в уравнения системы. Получим
n |
|
n |
n |
|
|
(Ci (x)zik (x) Ci (x)zik (x)) |
ak j (x) |
Ci (x)zij (x) |
fk (x), |
||
i 1 |
|
j 1 |
i |
1 |
|
|
(k 1,2,..., n) . |
|
|
||
Изменив порядок суммирования в правой части этого |
|||||
равенства, получим |
|
|
|
|
|
n |
|
n |
n |
|
|
(Ci (x)zik (x) Ci (x)zik (x)) |
Ci (x) |
ak j (x)zij (x) |
fk (x), |
||
i 1 |
|
i 1 |
j |
1 |
|
|
(k 1,2,..., n) . |
|
|
||
Запишем последнее равенство в виде |
|
|
|
||
n |
n |
n |
|
|
|
Ci (x)zik (x) |
Ci (x) zik (x) |
ak j (x)zij (x) |
fk (x), |
||
i 1 |
i 1 |
j |
1 |
|
|
(k 1,2,..., n) .
190

Принимая во внимание, то что |
zik (x) |
- |
фундаментальная система решений однородной системы уравнений, видим: выражение в квадратной скобке во второй сумме равно тождественно нулю. В результате мы приходим к следующей алгебраической системе уравнений для определения производных Ci (x)
n
Ci (x)zik (x) fk (x), (k 1,2,..., n)
i |
1 |
|
|
|
или в развернутом виде |
|
|
||
z11 (x)C1 (x) |
z12 (x)C2 (x) zn1 (x)Cn (x) |
f1 (x), |
|
|
z21 (x)C2 (x) |
z22 (x)C2 (x) zn2 (x)Cn (x) |
f 2 (x), |
(5.52) |
|
|
||||
|
||||
zn1 (x)C1 (x) |
zn2 (x)C2 (x) znn (x)Cn (x) |
f n (x). |
|
|
Определителем этой линейной системы уравнений является определитель Вронского, который, в силу линейной независимости функций zik (x) , отличен от нуля при x [a,b] .
Решая систему (5.52) методом Крамера, получим
|
n |
|
|
Wk i (x) |
|
|
|
Ci (x) |
|
|
fk (x) |
(i 1,2,..., n) , |
(5.53) |
||
|
|
W (x) |
|||||
k |
|
1 |
|
|
|
||
|
|
|
|
|
|
||
где W (x) - определитель |
Вронского (5.32), |
Wk i (x) - |
|||||
алгебраическое дополнение элемента zik (x) вронскиана W (x) . Отметим, что для удобства в формуле (5.53) вспомогательные
определители разложены по |
столбцу |
из |
свободных |
членов |
|||
f1 (x) , f 2 (x),..., |
f n (x) . |
|
|
|
|
|
|
Интегрируя (5.53), находим: |
|
|
|
||||
n |
x |
Wk i (x) |
|
|
|
|
|
Ci (x) |
f k (x) |
dx ci |
(i |
1,2,..., n) . |
(5.54) |
||
W (x) |
|||||||
k |
1x |
|
|
|
|
||
|
|
|
|
|
|||
|
0 |
|
|
|
|
|
|
Подставив эти значения Ci (x) |
в формулу (5.51), получаем: |
||||||
191

|
n |
n |
x |
W ji (x) |
|
n |
|
|
|
|
|||||
yk (x) |
zik (x) |
|
f j (x) |
|
dx |
ci zik (x), (k 1,2,..., n). (5.55) |
|
|
W (x) |
||||||
i |
1 |
j |
1x |
i |
1 |
||
|
|||||||
|
|
|
0 |
|
|
|
Формулы (5.55) определяют общее решение линейной неоднородной системы дифференциальных уравнений. Первые выражения в (5.60) дают частное решение неоднородной системы, а вторые выражения – общее решение соответствующей однородной системы уравнений.
Таким образом, задача интегрирования линейной неоднородной системы сводится к задаче построения фундаментальной системы решений соответствующей ей однородной системы уравнений и последующего нахождения квадратур.
Пример. Найти общее решение неоднородной системы
dy |
z , |
dz |
y |
1 |
ln x , |
|
|
|
|
||||
dx |
dx |
x2 |
||||
|
|
|
если известно общее решение соответствующей однородной системы
y C e x |
C |
2 |
e x , |
z C e x |
C |
2 |
e x . |
|
|||
|
1 |
|
|
|
1 |
|
|
|
|
||
Решение. Общее решение неоднородной системы ищем |
|||||||||||
методом вариации постоянных: |
|
|
|
|
|
|
|||||
y C (x)e x |
C |
2 |
(x)e x , z |
C (x)e x |
C |
2 |
(x)e x . |
(*) |
|||
1 |
|
|
|
|
1 |
|
|
|
|
||
Функции C1 (x) и C2 (x) определяем из системы уравнений:
C (x)e x |
C |
|
(x)e x |
0 , |
|
C (x)e x C |
|
(x)e x |
1 |
ln x . |
||||||||||||||||
2 |
|
2 |
|
|
|
|||||||||||||||||||||
|
|
|
||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
x2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Разрешим |
|
полученные |
уравнения |
относительно |
|||||||||||||||||||||
неизвестных |
|
|
функций |
|
C1 (x) и C2 (x) . Складывая эти |
|||||||||||||||||||||
уравнения, а затем вычитая из первого второе, получим: |
||||||||||||||||||||||||||
|
dC1 (x) |
|
1 |
e x |
|
1 |
|
|
ln x , |
dC2 (x) |
|
|
|
1 |
e x |
1 |
|
ln x . |
||||||||
|
dx |
2 |
|
x2 |
dx |
|
|
2 |
x2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Отсюда C |
|
(x) |
1 |
|
|
e x |
1 |
|
ln x dx |
|
c |
, |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1,2 |
|
|
|
|
2 |
|
|
|
|
x2 |
|
|
|
1,2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
192
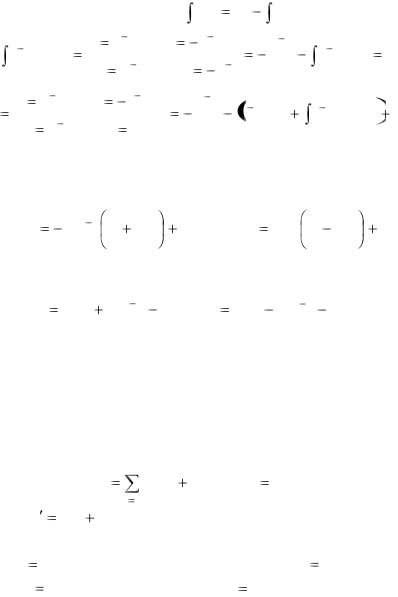
где |
|
c1,2 |
|
- |
|
произвольные |
постоянные. |
Используя |
метод |
|||||||||||||||||||||||||||||||
интегрирования по частям |
udv |
|
uv |
|
vdu , получим: |
|
|
|||||||||||||||||||||||||||||||||
e |
x |
1 |
|
dx |
|
|
u e x , du |
|
e x dx |
|
e x |
|
|
|
e |
|
x 1 |
dx |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
x2 |
|
|
dv x 2 dx, v |
|
|
x 1 |
|
|
x |
|
|
|
|
|
|
|
x |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
u |
|
e |
|
|
x , |
|
du |
|
|
|
|
e x dx |
|
|
e |
x |
|
|
e x ln x |
|
|
|
e |
|
x ln xdx |
c . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
dv |
|
x |
1 |
dx, |
v |
ln x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Подставляя |
|
|
вычисленный |
интеграл |
|
|
в |
выражение для |
|||||||||||||||||||||||||||||
C1 (x) и проделав аналогичную процедуру |
|
с |
интегралом, |
|||||||||||||||||||||||||||||||||||||
входящим в C2 (x) , получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
C (x) |
|
|
1 |
e |
x |
1 |
|
ln x c |
, |
C |
|
(x) |
1 |
|
e |
x |
1 |
|
|
ln x c |
|
. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|||||||||||||||||||||
1 |
|
|
|
|
2 |
|
|
|
x |
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Найденные функции подставим в выражения (*). То есть, |
|||||||||||||||||||||||||||||||||||||
общее решение системы записывается в виде: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
y c e x |
c |
|
|
e x ln x , |
|
|
z c e x |
|
c |
|
e x |
|
|
1 |
. |
|
|
|
|
||||||||||||||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5.5. Системы линейных дифференциальных уравнений с постоянными коэффициентами. Метод Эйлера построения фундаментальной системы решений
В данном разделе изучаются линейные системы дифференциальных уравнений вида (5.14), сокращенная форма записи которых следующая
|
|
dyk |
n |
|
|
|
|
|
|
|
|
|
|
ak i yi fk (x) |
(k |
1,2,..., n) |
(5.56) |
||||
|
|
dx |
i 1 |
|||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
или Y |
AY F(x) . |
|
|
|
|
|
|
|
||
Здесь постоянные |
вещественные |
коэффициенты ak i |
||||||||
(k,i |
1,2,..., n) - элементы матрицы |
A , |
Y |
colon(y1,..., yn ) , |
||||||
F (x) |
colon( f1,..., f n ) , |
f k (x) (k |
1,2,..., n) - |
непрерывные в |
||||||
(a,b) функции.
193

Из общей теории линейных систем уравнений, изложенной в предыдущих параграфах этой главы, следует существование решения этой системы и единственность решения начальной задачи. Здесь мы покажем, что систему (5.61) можно проинтегрировать в конечном виде, выражая решение либо через элементарные функции, либо в квадратурах.
В §5.5 было показано, что интегрирование неоднородной линейной системы приводится к интегрированию соответствующей однородной системы. Общее решение неоднородной системы линейных уравнений можно найти методом вариации постоянных, если известна фундаментальная система решений соответствующей однородной системы
|
|
|
|
dyk |
|
n |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
ak i yi |
|
(k |
1,2,..., n) , |
|
|
|
(5.57) |
|||||||
|
|
|
|
dx |
|
|
|
|
|
||||||||||
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
AY . |
|
|
|
|
|
|
|
(5.58) |
|
|
Ниже будет показано, что фундаментальная система |
||||||||||||||||||
решений может быть построена из |
элементарных функций, |
||||||||||||||||||
непрерывно дифференцируемых в интервале ( |
, |
) . |
|
||||||||||||||||
|
Построение фундаментальной системы решений и |
||||||||||||||||||
общего решения однородной линейной системы. |
|
|
|
||||||||||||||||
|
Частное решение системы (5.57) будем искать в виде |
||||||||||||||||||
|
|
y |
1 |
e |
x , |
y |
2 |
2 |
e x ,..., |
y |
n |
n |
e |
x |
|
(5.59) |
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
или, что тоже самое, в векторной форме |
|
|
|
|
|
||||||||||||||
|
|
Y |
e |
|
x , |
|
colon( |
1, |
2 ,..., |
n ) , |
|
|
(5.60) |
||||||
где |
1, |
2 ,..., |
n |
|
и |
- некоторые постоянные, причем числа |
|||||||||||||
1, |
2 ,..., |
n |
не |
|
|
равны |
|
нулю |
|
одновременно |
(при |
||||||||
1 |
2 |
... |
n |
|
0 |
получили бы нулевое решение, |
которое |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
не может входить в фундаментальную систему решений). |
|||||||||||||||||||
|
Необходимо найти постоянные |
1, |
2 , ..., |
n и |
так, |
||||||||||||||
194
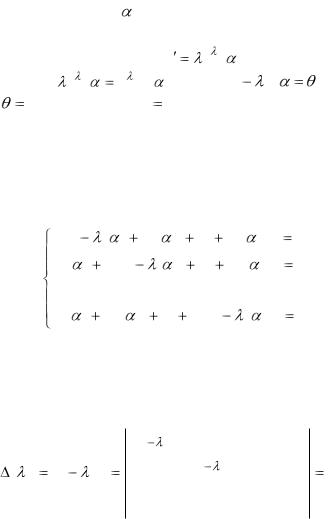
чтобы функции yk 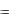 k e
k e x удовлетворяли системе (5.57) .
x удовлетворяли системе (5.57) .
|
Подставляя в векторное уравнение (5.58) искомое |
|||||||
решение (5.60) и учитывая Y |
e |
x , находим |
|
|
||||
|
e x |
e |
x A |
, |
или |
(A E) |
, |
(5.61) |
где |
colon(0,0,...,0) , |
E |
diag(1,1,...,1) . |
|
|
|||
Равенство (5.61) показывает: функция (5.60) является решением рассматриваемой однородной системы в том случае, когда  - собственное число матрицы,
- собственное число матрицы, 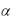 - принадлежащий этому собственному числу собственный вектор этой матрицы.
- принадлежащий этому собственному числу собственный вектор этой матрицы.
В координатной форме уравнения (5.61) представляет собой однородную систему линейных уравнений вида
(a11 |
) 1 a12 2 a1n n |
|
a21 1 (a22 |
) 2 a2n n |
|
0,
0,
(5.62)
an1 1 an2 2 (ann |
) n |
0. |
Отметим, что систему (5.62) можно получить и непосредственно, минуя операции в матричной форме, если подставить функции (5.59) в уравнения (5.57).
Будем искать решения отличные от нулевого. При этом определитель системы (5.62) должен быть равен нулю, то есть
|
|
|
|
a11 |
a12 |
|
a1n |
|
( ) |
|
A E |
|
a21 |
a22 |
|
a2n |
0 . (5.63) |
|
|
|||||||
|
|
|
|
|
|
|||
|
|
|
|
|
an1 an2 ann 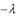
Алгебраическое уравнение (5.63) называется характеристическим уравнением для системы типа (5.57) с постоянными коэффициентами aij .
Среди корней характеристического многочлена с действительными коэффициентами в правой части (5.63) могут быть:
195
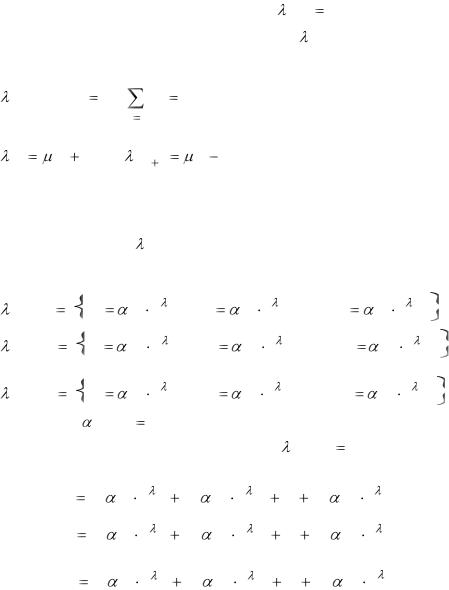
|
1) |
простые действительные корни |
i , (i |
1,2,...n ) ; |
|
||
|
2) |
кратные действительные корни |
k |
кратности |
S k , |
||
при |
этом сумма |
всех |
кратностей, включая |
простые |
корни |
||
|
|
|
l |
|
|
|
|
m |
с |
Sm 1, |
S j |
n, где l - число различных корней; |
|||
j1
3)среди корней есть комплексно-сопряженные пары
m |
|
|
m |
ivm , |
|
m 1 |
|
|
m ivm , |
|
|
|
|
|
|
|
|
|
|||
простые или кратные. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Соответственно этим случаем Y (k ) |
из (5.59) могут иметь |
||||||||||||||||||||
следующий вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1. |
|
|
Все |
|
i |
- действительные и различные. |
|
||||||||||||||
Тогда фундаментальная система решений может быть |
|||||||||||||||||||||
записана следующим образом: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
: Y (1) |
|
y(1) |
(1) |
e 1x ; y(1) |
|
(1) |
e 1x ; ; y |
(1) |
|
(1) e 1x , |
|
||||||||||
1 |
|
|
|
1 |
1 |
|
|
|
|
2 |
|
2 |
|
|
|
|
n |
|
n |
|
|
:Y (2) |
|
y(2) |
(2) |
e |
2x ; y(2) |
|
(2) |
e |
2x ; ; y(2) |
(2) e 2x |
, |
||||||||||
2 |
|
|
|
1 |
1 |
|
|
|
|
2 |
|
2 |
|
|
|
|
|
n |
|
n |
|
.......... .......... .......... .......... .......... .......... .......... .......... .......... .......... ....... |
|
||||||||||||||||||||
: Y (n) |
|
y(n) |
(n) |
e |
nx ; y(n) |
|
(n) |
e |
nx ; ; y(n) |
(n) e nx . |
|||||||||||
n |
|
|
|
1 |
1 |
|
|
|
|
2 |
|
2 |
|
|
|
|
|
n |
|
n |
|
Здесь |
(k ), (i |
1, ..., n) |
находятся для каждого Y (k ) из |
|
|||||||||||||||||
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.62) при соответствующем значении |
k |
(k |
|
1, ..., n). При |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
этом общее решение (5.58) |
|
для данного случая имеет вид |
|
||||||||||||||||||
y (x) |
C |
(1) |
e |
1x |
C |
2 |
(2) |
e 2x |
C |
n |
|
(n) |
e nx ; |
|
|||||||
|
1 |
|
1 |
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
||||||
y |
2 |
(x) |
C |
(1) |
e |
1x |
C |
2 |
(2) |
e 2x |
C |
n |
|
(n) |
e nx ; |
|
|||||
|
|
1 |
21 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
||||||
.......... .......... .......... .......... .......... .......... .......... .......... .......... . |
|
||||||||||||||||||||
y |
n |
(x) |
C |
(1) |
e |
1x |
C |
2 |
(2) |
e 2x |
C |
n |
|
(n) |
e nx . |
|
|||||
|
|
|
1 |
n |
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|||
Пример 1. Найти общее решение однородной линейной системы дифференциальных уравнений с постоянными коэффициентами
196
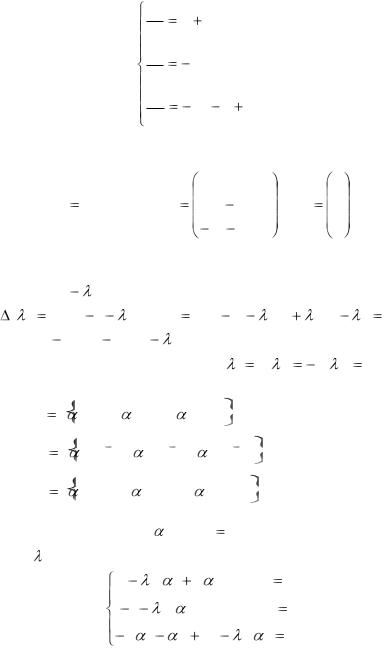
dy |
y 2z |
|
dx |
||
|
||
dz |
z |
|
dx |
||
|
||
du |
2 y z 2u. |
|
dx |
||
|
Решение. В матричной форме эту систему можно записать следующим образом:
dX |
|
|
1 |
2 |
0 |
|
x |
|
AX , |
где A |
0 |
1 |
0 |
, X |
y . |
||
|
||||||||
dt |
||||||||
|
|
2 |
1 |
2 |
|
z |
||
|
|
|
|
Запишем характеристическое уравнение (5.63) для этой системы
|
|
1 |
2 |
0 |
|
|
|
|
|
|
|
|
( ) |
|
0 |
1 |
0 |
0; |
(1 |
|
)(1 |
)(2 |
|
) |
0 . |
|
|
2 |
1 |
2 |
|
|
|
|
|
|
|
|
Корни |
|
этого |
уравнения |
1 |
1; |
2 |
1; |
3 |
2 |
все |
||
|
|
|
|
|
|
|
|
|
|
|||
действительные и различные, следовательно
Y (1) |
|
1(1)e x ; |
2(1)e x ; |
3(1)e x |
, |
|
|
||
Y (2) |
1(2)e x ; |
|
2(2)e x ; |
3(2)e x |
, |
|
|||
Y (3) |
1(3)e2x ; |
|
2(3)e2x ; |
3(2)e2x . |
|
|
|||
Найдем |
из (5.62) |
(1) , |
(i |
1, 2, 3) , |
соответствующие |
||||
|
|
|
|
i |
|
|
|
|
|
корню |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1 |
|
1 ) 1 |
|
2 2 |
|
|
0 |
|
|
( |
1 |
1 ) |
2 |
|
|
|
0 |
|
|
|
2 |
1 |
2 |
(2 |
1 ) |
3 |
0. |
197

Так как определитель этой системы ( 1) 0 , то одно из
неизвестных можно взять в качестве произвольного параметра, поскольку
|
|
|
|
|
|
|
|
|
|
|
M ij |
|
|
0 |
|
|
|
2 |
|
0 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
и ранг этой системы равен двум. Пусть |
|
|
3 |
|
|
1 , |
тогда 2 |
0 и |
||||||||||||||||||||||||||
|
|
1 |
. |
Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Y |
(1) |
(t) |
|
1 |
e |
x |
; |
0; |
e |
x |
. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для определения |
|
i2, |
(i |
1,2,3) получим |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
(1 |
|
|
|
2) |
1 |
2 |
2 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
0 |
|
0 . |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
( |
1 |
|
2) |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2 |
|
|
|
|
|
|
|
, |
|
|
( |
2) |
|
|
|
|
0 |
0 |
0 |
|
|||||||||||||
|
2 |
|
|
|
(2 |
|
|
2 ) |
|
|
0 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
3 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Так |
как |
( |
|
2 ) |
0, положим |
|
|
|
|
2 |
|
|
1, |
при |
этом |
||||||||||||||||||
Mij |
|
0 |
|
0, |
|
поэтому |
|
|
|
|
|
|
2 |
1 |
|
|
0 |
3 |
2 |
2 |
и |
|||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
2 |
1 |
|
|
3 |
3 |
2 |
|
|||||||||||||
следовательно |
1 |
|
1; |
3 |
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Y (2) |
|
|
e x ; e x ; e x . |
|
|
|
|
|
|
|
|||||||||||||||
|
Аналогично |
для |
нахождения |
|
|
(3) |
, (i |
|
|
1,...,3) |
будет |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
(1 |
|
|
|
3) |
1 |
2 |
2 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
( |
1 |
|
3) |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 . |
|||||||
|
|
2 |
|
|
|
|
|
|
|
, |
|
|
( |
3) |
|
|
|
|
0 |
3 |
0 |
|
||||||||||||
|
2 |
|
|
|
(2 |
|
|
3 ) |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
1 |
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
0 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пусть |
3 |
1, |
тогда |
2 |
|
1 |
|
0, поэтому |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Y (3) |
|
|
|
|
0; |
0; |
|
|
e2x . |
|
|
|
|
|
|
|
||||||
198

Общее решение системы будет иметь вид
y(x) |
|
1 |
C e x |
C |
e x , |
|
||
|
|
|
||||||
|
2 |
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
||
z(x) |
C2e x , |
|
|
|
|
|||
u(x) |
C e x |
C |
e |
x C |
e2x . |
|||
|
1 |
|
2 |
|
3 |
|
||
2. Рассмотрим случай, когда среди действительных корней есть кратные.
Пусть корень k имеет кратность S k , тогда этому корню в фундаментальной системе решений будут соответствовать S k строк:
k: Y (k)
:Y (k 1)
(k) |
e k x ; |
(k) |
e |
k x ; ...; |
(k) |
e |
k x |
; |
1 |
|
2 |
|
|
n |
|
|
|
(k 1) |
x e k x ; |
(k |
1) |
x e k x ; ...; |
(k |
1) x e k x ; |
||
1 |
|
2 |
|
|
|
n |
|
|
……………………………………………………………..
: Y (k Sk 1) |
(k |
Sk |
1) |
xSk |
1e k x; |
(k |
Sk 1) |
xSk 1e |
k x; ...; |
(k |
Sk |
1) |
xSk 1e k x . |
||||||
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
n |
|
|
|
|
Пример 2. |
Найти |
общее |
|
|
решение |
|
|
системы |
||||||||||
дифференциальных |
уравнений |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
dy |
2 y |
z |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
d |
y |
2 |
1 |
|
y |
|||||
|
|
|
dx |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
dz |
|
|
|
|
|
или |
|
|
|
z |
1 |
0 |
|
z . |
||
|
|
|
|
y |
|
|
|
dx |
|
||||||||||
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Решение. Характеристическое уравнение этой системы |
||||||||||||||||||
будет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
) |
|
|
|
|
1 |
|
0, |
то |
есть |
2 |
2 |
1 |
0 |
||||
|
|
2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
1 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
1 |
2 |
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Запишем фундаментальную систему решений |
|
|
|
|||||||||||||||
Y (1) |
|
(1) |
|
ex |
; |
(1) |
ex ; |
|
Y (2) |
|
(2) x ex ; |
(2) |
x ex . . |
||||||
|
|
1 |
|
|
|
|
2 |
|
|
|
|
1 |
|
|
2 |
|
|
||
199
