БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Шипачев В.С. Высшая математика / В.С. Шипачев. 
М.: Наука, 2000.
2.Пискунов Н.С. Дифференциальное и интегральное исчисление / Н.С. Пискунов. М.: Наука, 1978. Т. 1.
3.Бугров Я.С. Дифференциальные уравнения. Ряды.
Функции комплексного переменного / Я.С. Бугров, С.М. Никольский. М.: Наука, 1989. 448 с.
4.Карташев А.П. Обыкновенные дифференциальные
уравнения и основы вариационного исчисления / А.П. Карташев, Б.А. Рождественский. – М.: Наука , 1976. 256 с.
5.Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление / Л.Э. Эльсгольц. – М.: Наука , 1969. 424 с.
6.Данко П.Е. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова - М.:
Высш. шк., 1986. Ч. 2. – 415 c.
7.Ризниченко Г.Ю. Математические модели в биофизике
иэкологии / Г.Ю. Резниченко. – М.: Институт компьютерных исследований, 2003. 184 с.
8.Самойленко А.М. Дифференциальные уравнения. Примеры и задачи / А.М. Самойленко, С.А. Кривошея, Н.А. Перестюк. – Киев: Вища школа, 1984. 408 с.
9.Найфэ А. Введение в методы возмущений / А. Найфэ. –
М.: Мир, 1984. 535 с.
10.Ли Цзун-дао. Математические методы в физике / Цзун-дао Ли. – М.: Мир, 1965. 296 с.
11. |
Вержбицкий |
В.М. Численные |
методы / |
В.М. Вержбцкий. – М.: Высш. шк., 2001. 382 с.
12. Амосов А.А. Вычислительные методы для инженеров/ А.А. Амосов, Ю.А. Дубинский, Н.В. Копченова – М: Высш.
шк., 1994. 544 с.


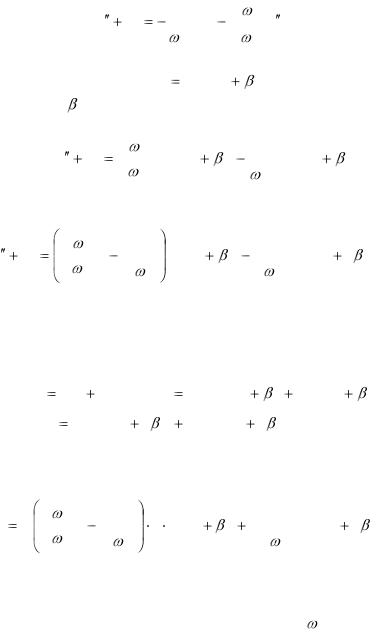
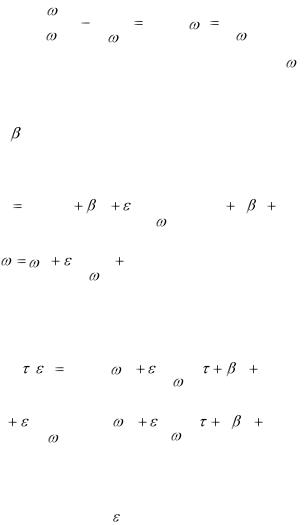
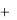 ).
).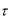
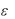 будет равномерно пригодным разложением первого порядка, поскольку в нем отсутствуют секулярные члены, а поправка (член пропорциональный ) оказывается малой по сравнению с главным членом разложения.
будет равномерно пригодным разложением первого порядка, поскольку в нем отсутствуют секулярные члены, а поправка (член пропорциональный ) оказывается малой по сравнению с главным членом разложения.