3447

Пример. Найти решение уравнения, удовлетворяющее начальным условиям

3*. Введем понятие о граничной (краевой) задаче.

Многие задачи физики, баллистики и других естественных и технических наук приводят к решению граничных задач для обыкновенных дифференциальных уравнений. Сформулированная в п.2 задача Коши является лишь одной из важных задач теории дифференциальных уравнений, в которых ищется решение, удовлетворяющее заданным условиям. В краевых задачах условия, налагаемые на искомое решение, задаются не в одной точке (как в задаче Коши), а на концах заданного интервала [a,b] . Решение в

этом случае ищется внутри интервала, на концах которого оно обязано удовлетворять определенным условиям.

В случае дифференциального уравнения первого порядка граничные задачи, вообще говоря, ставятся не так, так как в

100

этом случае задание значения искомого решения в одной точке (при определенных условиях, сформулированных ранее) уже определяют единственную интегральную кривую. Таким образом, граничные задачи могут ставиться только для уравнений второго и более высокого порядка.

Граничные задачи не всегда имеют решение, а если решение и существует, то, весьма часто, не единственное.

Пример. Найти решение краевой задачи: y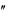 6x ,

существует решения, удовлетворяющего краевым условиям:

постоянные. Наша задача заключается в таком выборе этих

101

Поскольку записанная выше функция включает все решения уравнения, то поставленная краевая задача не имеет решения, ибо мы получили противоречивую систему

множество решений. Действительно, в этом случае система уравнений для определения параметров имеет вид:

6. y C1(x C2 )2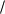3 , ( y )2 2yy 0.

Из решений предшествующих задач выделить частные решения со следующими начальными условиями:

102

(см. пример в п.3).

3.2. Достаточные условия существования и единственности решения задачи Коши. Общее частное решение

1*. Для дифференциального уравнения n -го порядка также доказана теорема существования и единственности решения задачи Коши. Здесь не приводится доказательство этой теоремы, а лишь формулируются достаточные условия существования и единственности решения начальной задачи в упрощенной форме для уравнения, разрешенного относительно старшей производной.

Теорема (Пикара). Пусть дано уравнение

103

При этих условиях дифференциальное уравнение имеет единственное решение y y(x) , удовлетворяющее заданным начальным условиям. Это решение определено и непрерывно вместе с производными до n - го порядка включительно в интервале

аргументов, то при любых начальных данных существует единственное решение уравнения с этими начальными данными.

2. Общее, частное и особое решение.

Соображения, приведенные в п.1, §3.1 для дифференциального уравнения 2-го порядка, связанные с исключением параметров C1 и C2 , позволяют и

104

дифференциальное уравнение (3.14) или (3.1) рассматривать

последующим исключением параметров из полученной системы n 1 уравнений.

Таким образом, можно считать, что общее решение дифференциального уравнения n - го порядка должно содержать n независимых параметров C1, C2 , , Cn .

ющих значениях этих параметров могут быть получены все решения уравнения, кроме особых.

Приведем более подробное определение*, в котором “расшифрованы” все условия, содержащиеся в выше приведенном.

Пусть D - область в каждой точке которой задача Коши для уравнения (3.14) имеет единственное решение.

y0(n 1) 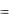(n 1) (x0 , C1, C2 , , Cn )

единственным образом разрешима относительно C1, , Cn :

105

C10 1(x0 , y0 , y0 , , y0(n 1) ) ,

Cn0 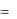n (x0 , y0 , y0 , , y0(n 1) ) ;

3)функция (x, C10 , , Cn0 ) является решением

уравнения (3.14) при любых значениях произвольных

называется общим решением в форме Коши.

Интегрируя уравнение (3.14) редко удается получить решение, зависящее от n произвольных параметров, в виде (3.15). В большинстве случаев n - параметрическое семейство интегральных кривых получается в неявном виде (в виде, не разрешенном относительно неизвестной функции y ):

(3.14) называются решения, полученные из общего решения при частных числовых значениях произвольных постоянных C1, , Cn , включая случай, когда значения этих констант

106

равны 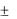: y 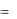(x, C10 , , Cn0 ) .

Аналогично вводится понятие частного интеграла – это решение в неявном виде, полученное из общего интеграла

уравнения, в каждой точке которого нарушается единственность решения задачи Коши.

Уравнение n го порядка (3.14) может иметь семейство особых решений, зависящее от произвольных постоянных,

функцию дифференциальное уравнение будет эквивалентно системе уравнений с разделяющимися переменными:

Другим решением этого уравнения является функция z 0.

Подставим найденные функции во второе уравнение. Получим совокупность уравнений

107

Интегрируя эти уравнения, будем иметь:

Таким образом, семейство решений y C не получается из общего решения уравнения ни при каких значениях постоянных C1 и C2 . Каждая из линий этого семейства

является особым решением уравнения.

Итак, для данного дифференциального уравнения получено общее решение – двухпараметрическое семейство интегральных кривых, а также построены особые решения.

Пример. Для дифференциального уравнения, заданного

впредыдущем примере, найти частное решение,

удовлетворяющее начальным условиям: y(0) 1, y (0) 0.

Решение. Из общего решения уравнения и его производной получим систему уравнений для нахождения постоянных C1 и C2 :

C1 0, C2 1.

Подставляя найденные постоянные в формулу для общего решения, получим частное решение, удовлетворяющее заданным начальным условиям:

108

3.3. Уравнения высших порядков, интегрируемые в квадратурах. Уравнения, допускающие понижения порядка

1. Из того, что дифференциальное уравнение n -го порядка (3.14) имеет решение, вовсе не следует, что решение выражается в квадратурах. Это замечание относится даже к уравнениям первого порядка. В этом параграфе будут указаны некоторые виды уравнений n -го порядка, общий интеграл которых, (или общее решение) можно найти при помощи квадратур.

Интегрирование таких уравнений будет осуществляться сведением к уравнениям низшего порядка. При такой процедуре порядки промежуточных дифференциальных уравнений постепенно понижаются, а число входящих в них параметров C1, C2 , (“произвольных постоянных”) – увеличивается. Интегрирование уравнения будет закончено когда получается общий интеграл Ф(x, y, C1 , , Cn ) 0 , не

содержащий производных искомой функции и включающий n произвольных постоянных.

Ниже будем рассматривать неполные уравнения, т.е. уравнения вида (3.14) но такие, в которых функция, стоящая в правой части, зависит только от некоторых аргументов.

2. Уравнение, содержащее старшую производную неизвестной функции и заданную функцию от x .

а)* Рассмотрим решение уравнения (3.14) в том случае,

записать уравнение (3.21) так:

dy(n 1) (x), dx

109