
3447
.pdf
ческую последовательность, называется асимптотическим
разложением функции |
f ( ) , если при |
|
0 |
|
||||
f ( |
) |
an |
n ( |
) |
o( |
n ( |
)) |
(7.12) |
|
n |
0 |
|
|
|
|
|
|
или, что, то же самое, |
|
|
|
|
|
|
|
|
|
N 1 |
|
|
|
|
|
|
|
f ( |
) |
an n ( |
) |
о( |
n ( |
)) . |
(7.13) |
|
|
n |
0 |
|
|
|
|
|
|
Этот факт записывается в виде |
|
|
|
|
|
|||
f ( |
) |
an |
n ( |
) |
при |
0. |
|
|
n 0
Отметим, что функция f ( ) может быть представлена
бесконечным числом асимптотических разложений.
При построении приближенных решений различного вида уравнений, а также при оценке интегралов предполагается обычно, что такие разложения можно подставлять в уравнения и выполнять арифметические действия, а также дифференцирование и интегрирование. Иногда применение некоторых из этих операций необоснованно. В этом случае они приводят к сингулярностям или неравномерностям.
Пример. Равенство
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
||||||||||||
|
x |
|
|
x |
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
... |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
x |
|
2 x |
|
|
|
|
2 |
|
|
|
|
x |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
x 1 |
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2x |
|
8x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
не обоснованно |
|
при |
|
|
x |
O(1) , |
т.к. |
|
второй, |
третий и |
||||||||||||||||||||
последующие члены разложения сравнимы по порядку величины с первым членом. Поэтому ошибка, совершаемая при
240
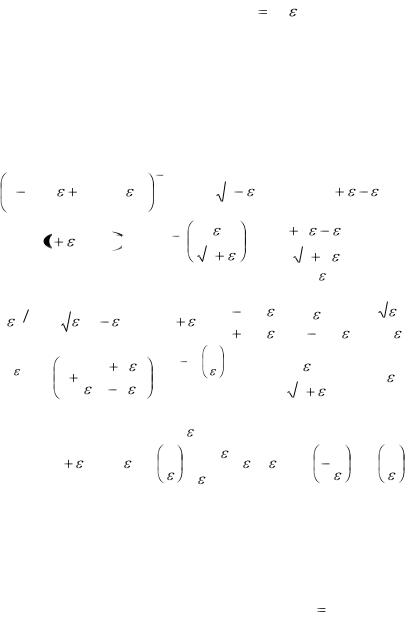
усечении ряда после N членов при x O( ) не будет иметь
порядок O(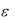 N ) , т.е. не будет порядка первого отброшенного
N ) , т.е. не будет порядка первого отброшенного
члена. В этом случае говорят о неравномерном разложении. Одна из главных целей метода возмущений проверка равномерности разложения.
Задачи для самостоятельного решения
1. Определить первые три члена разложения при малом 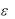 :
:
|
|
3 |
|
4 |
|
51 |
|
|
4 |
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||
1 |
a |
|
a |
|
|
; |
|
cos |
1 |
|
|
|
t ; |
|
|
|
|
|
sin(1 |
|
|
|
); |
|
||||||||||||||||||||||||||||
8 |
|
256 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
1 ; |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
cos x |
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
; ln |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2. Определить порядок функции при малых |
: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/ 2 |
|
|
|
|
|
|
|
|
|
|
|
|||
100 |
1 2 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
(1 |
|
|
); |
|
ln(1 |
|
); |
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
; |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
cos |
|
|
|
1 |
cos |
|
|
|
|
sin |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ch |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
etg |
; |
|
ln 1 |
|
|
ln(1 |
|
2 |
|
) |
; |
|
e |
|
|
; |
|
|
|
arcsin |
|
|
|
|
|
|
; |
|
ln(ctg |
|
). |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
(1 |
|
2 |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3. Расположить |
данные |
|
выражения |
в |
|
ряд по |
порядку |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
убывания при малых |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
ln(1 |
|
|
), ctg , |
th |
|
1 |
|
, |
|
|
sin |
|
|
|
, |
ln |
, |
|
exp |
|
1 |
, |
sh |
1 |
. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 / 4 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
7.5. Простейшие асимптотические методы решения дифференциальных уравнений
Во многих задачах механики колебания консервативных систем с одной степенью свободы описываются дифференциальными уравнениями вида
y0 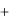 f ( y) 0 ,
f ( y) 0 ,
(7.14)
241

где y – |
перемещение, f (y) – некоторая |
нелинейная |
функция |
от y – восстанавливающая сила, |
y – ускорение. |
Точками над буквой обозначены производные по времени t .
Пусть y y0 |
определяет |
положение |
равновесия системы. |
||||||||||||||||
Тогда f ( y0 ) |
0 . Предположим, что |
|
функцию f (y) в |
||||||||||||||||
окрестности точки y0 можно разложить в ряд Тейлора |
|
||||||||||||||||||
|
|
f ( y) |
k ( y y |
0 |
) k |
2 |
( y y |
0 |
)2 |
k |
3 |
( y y |
0 |
)3 |
, |
||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
где |
kn |
|
1 |
|
d n f ( y0 ) |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
n! |
dyn |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Если считать, что восстанавливающая сила является |
||||||||||||||||||
нечетной функцией смещения от равновесия |
f ( y) |
f ( y) |
|||||||||||||||||
(т.е. пружина ведет себя одинаково при растяжении и сжатии),
и ограничиться в разложении функции |
|
f (y) двумя членами, то |
|||
уравнение (7.14) примет вид |
|
|
|
|
|
x k x k |
3 |
x3 |
0 |
, |
(7.15) |
1 |
|
|
|
|
|
где x y y0 . Уравнение |
|
(7.15) |
обычно называют |
||
уравнением Дюффинга.
Введем характерные масштабы задачи – линейный X и временной T , и перейдем к безразмерным переменным
|
|
|
|
|
u |
x |
, |
|
|
|
t |
. |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
X |
|
|
|
T |
|
|
|
|
|
|
|
|
|||||
Используем |
|
правило |
дифференцирование сложной |
|||||||||||||||||||||
функции для перехода к новым переменным |
|
|
|
|
||||||||||||||||||||
|
d |
|
d |
|
d |
|
1 |
|
|
|
d |
|
, |
|
d 2 |
|
1 |
|
|
d |
. |
|
|
|
|
dt dt d |
T d |
|
|
dt 2 |
|
T 2 d |
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
Тогда уравнение (7.15) преобразуется к виду |
|
|
|
|
||||||||||||||||||||
|
|
|
u |
|
k T 2u k T 2 X 2u3 |
0 . |
|
|
|
|
|
|
||||||||||||
|
|
|
|
1 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Введем обозначения |
2 |
|
k T 2 , |
|
|
|
k T 2 X 2 |
, где |
0 |
и |
||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
1 |
|
|
|
3 |
|
|
|
|
|
|||||
- безразмерные |
параметры, |
|
- |
|
|
характеризует |
|
степень |
||||||||||||||||
242

нелинейности системы, точка над буквой обозначает дифференцирование по  .
.
Тогда уравнение преобразуется к виду
|
|
|
|
|
|
|
|
u |
|
|
2u |
|
u3 |
0 . |
|
|
|
|
(7.16) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
В качестве начальных условий примем |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
u(0) u0 , |
|
u(0) u1. |
|
|
|
|
(7.17) |
||||||||||
|
Прямое разложение. Неравномерность разложения. |
|||||||||||||||||||||
|
Решение уравнения Дюффинга (8.16) отыскиваем в виде |
|||||||||||||||||||||
ряда по степеням параметра |
|
|
, |
который считаем малым |
||||||||||||||||||
|
|
|
u( , |
) |
|
u |
0 |
( |
) |
|
|
u ( |
|
) |
2u |
2 |
( ) |
|
. |
(7.18) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
Ограничившись в решении членом правого порядка малости |
||||||||||||||||||||||
|
|
|
|
u( , |
|
) = u |
0 |
( |
) |
|
|
u ( |
) |
O( |
2 ) , |
|
(7.19) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
подставим (7.19) в уравнение (7.16) учитывая равенство |
||||||||||||||||||||||
(u |
0 |
|
|
u ( ) O( 2 ))3 |
u3 |
3u 2 ( u O( 2 )) |
|
|
||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
0 |
|
0 |
1 |
|
|
|
|
|||
3u |
0 |
( u O( 2 ))2 |
|
( u ( ) O( 2 ))3 |
u3 |
3 u 2 u O( 2 ). |
||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
0 |
0 |
1 |
|
Получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
u |
2u |
0 |
|
|
(u |
|
|
|
2u |
u 3) |
O( |
2 ) |
0 . |
(7.20) |
||||||
|
|
|
0 |
0 |
|
|
|
|
1 |
|
|
0 |
1 |
|
0 |
|
|
|
|
|
||
|
Полагая в (7.19) |
|
|
|
0 имеем уравнение для первого члена |
|||||||||||||||||
разложения (7.18) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
u |
|
|
|
2u |
0 |
0 . |
|
|
|
|
|
(7.21) |
|||
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
||
Его решение, как известно, имеет вид |
|
|
|
|
|
|||||||||||||||||
u0 ( |
) |
C1 cos |
|
0 |
|
C2 sin |
0 |
a0 cos( |
0 |
0) , |
(7.22) |
|||||||||||
где a0 |
|
и |
0 – произвольные постоянные. |
|
|
|
||||||||||||||||
|
Учитывая (7.21), уравнение (7.20) |
принимает форму |
||||||||||||||||||||
|
|
|
|
|
|
|
(u |
|
|
|
2u u |
3 ) O( 2) 0 . |
|
|
||||||||
|
|
|
|
|
|
|
|
1 |
|
|
0 |
1 |
|
0 |
|
|
|
|
|
|
||
|
Разделим |
на |
|
|
, |
|
а |
затем |
положим |
|
0 . Учтя, что |
|||||||||||
1O( 2 ) |
O( ) и что O( |
|
0) |
0 , получим уравнения для |
||||||||||||||||||
функции |
u1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
243
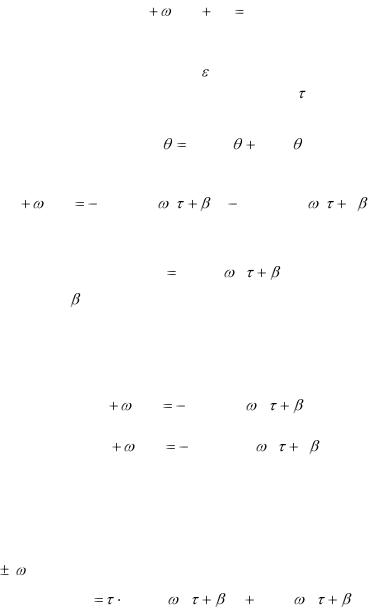
u |
2u |
u3 |
0 . |
(7.23) |
|
1 |
0 |
1 |
0 |
|
|
Отметим, что и уравнение (7.20) и уравнение (7.23) можно получить из (7.20), если приравнять нулю коэффициенты при последовательных степенях .
Подставим в уравнение (7.23) u0 ( ) в виде (7.22) и принимая во внимание элементарное равенство
|
|
|
|
|
cos3 |
|
|
1 |
cos3 |
|
|
|
3 |
cos , |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
4 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
перепишем (7.23) в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
u |
2u |
|
3 |
a3 cos( |
|
|
|
|
) |
|
1 |
a3 cos(3 |
|
3 |
|
) . (7.24) |
|||
|
|
0 |
0 |
|
0 |
0 |
|||||||||||||
1 |
0 |
1 |
4 |
0 |
|
4 |
|
0 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решения |
|
|
соответствующего |
|
уравнению |
|
(7.24) |
||||||||||||
однородного уравнения имеет вид |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
u1(одн) |
|
a1 cos( |
0 |
|
1), |
|
|
|
(7.25) |
|||||
где a1 |
и |
1 – произвольные постоянные. |
|
|
|
|
|||||||||||||
В |
силу |
линейности |
уравнения |
(7.24) |
частное |
решение |
|||||||||||||
этого неоднородного уравнения можно записать в виде суммы двух частных решений, соответствующих каждому из слагаемых в правой части
u |
2u |
3 |
a3 cos( |
|
|
) , |
|
(7.26) |
|||
|
|
0 |
0 |
|
|||||||
1 |
0 |
1 |
4 |
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
u |
2u |
|
1 |
a3 cos(3 |
|
3 |
|
) . |
(7.27) |
||
|
|
0 |
0 |
||||||||
1 |
0 |
1 |
4 |
0 |
|
|
|
||||
|
|
|
|
|
|
|
|
||||
Оба этих уравнения имеют правую часть специального вида. Поэтому частные решения моделируются, а затем применяется метод неопределенных коэффициентов как это показано в курсе дифференциальных уравнений. Для уравнения (7.26) корни характеристического уравнения равны
i 0 , поэтому частное решение записывается в виде
u (1) |
( Acos( |
0 |
0 |
) B sin( |
0 |
0 |
)) . |
|
|
1 |
|
|
|
|
|
||||
Подставляя |
в уравнение |
|
(7.26) |
и применяя |
метод |
||||
неопределенных |
коэффициентов |
для |
отыскания |
А |
и В, |
||||
244

получим
|
(1) |
3 |
|
a3 |
|
|
|
|
|
u |
|
|
0 |
sin( |
0 |
0 |
) . |
(7.28) |
|
|
|
|
|||||||
1 |
8 |
|
|
|
|
|
|||
|
|
0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
Аналогично для уравнения (7.27) получим частное решение в виде
u |
(2) |
|
a03 |
|
cos(3 |
0 |
3 |
0 |
) . |
(7.29) |
|
|
|
|
|||||||
1 |
4(9 |
02 |
1) |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
Складывая общее решение однородного уравнения (7.25) и частные решения (7.28) и (7.29) получим общее решение
уравнения (7.24) |
в виде |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
3 a3 |
|
|
|
|||
u ( ) |
a cos( |
0 |
0 |
) |
|
|
0 |
sin( |
0 |
0 |
) |
|||||
|
|
|||||||||||||||
1 |
1 |
|
|
|
8 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
(7.30) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
a03 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
cos(3 |
0 |
3 0). |
|
|
|
|||||
|
4 9 |
2 |
|
|
|
|
|
|||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя u0 |
и u1 из (7.22) и (7.30) в разложении (7.19) |
|||||||||||||||
для общего решения уравнения (7.16) получаем следующее разложение первого порядка
|
|
|
u1 ( , |
) = a0 cos( 0 |
|
0) |
(a1 cos( |
0 |
1) |
||||||
|
3 a03 |
|
|
1 |
|
|
a03 |
|
|
|
|
|
|||
- |
|
|
|
sin( |
0 |
0) + |
|
|
|
|
|
cos(3 0 |
3 0) )+… , (7.31) |
||
8 |
|
|
4 9 |
2 |
|
||||||||||
|
0 |
|
|
|
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
где |
|
a0 , a1, |
0, |
1– произвольные |
постоянные. |
Хотя мы |
|||||||||
получили четыре постоянных, но оказывается, что они связаны между собой и для их нахождения вполне достаточно двух начальных условий. Действительно, подставляя разложение (7.31) в условия (7.17), получаем
u0 a0 cos 0 |
(a1 cos |
1 |
1 |
|
|
a03 |
|
cos3 |
0) ... . |
4 |
|
|
2 |
|
|||||
|
|
|
9 |
1 |
|
||||
|
|
|
|
|
|
0 |
|
|
|
245

u |
a |
0 |
0 |
sin |
|
(a |
0 |
sin |
|
3 a30 |
sin |
|
3 |
|
a30 |
|
0 |
|
sin 3 |
|
) ... |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
|
|
0 |
1 |
|
1 |
8 |
|
|
|
0 |
4 |
9 |
2 |
1 |
|
0 |
|
|||||
|
|
|
|
|
|
|
|
0 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
Приравнивая члены при одинаковых степенях 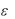 в левой и правой частях этих равенств, получим
в левой и правой частях этих равенств, получим
|
|
|
|
u0 |
|
|
a0 cos |
0 ; |
|
|
|
|
|
|
|
u1 |
|
|
|
|
a0 sin |
0 , |
|
|
|
|
|
(7.32) |
|||||||||||||||
|
|
|
|
a1 cos |
|
|
|
|
|
1 |
|
|
|
|
|
a30 |
|
|
cos3 0 , |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
1 |
|
|
4 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
a1 0 sin |
|
|
|
|
3 |
|
a30 |
sin |
|
|
|
|
3 |
|
a30 |
0 |
|
sin 3 |
|
0 . |
|
|
|
|
|
(7.33) |
|||||||||||||||||
1 |
8 |
|
|
0 |
|
|
|
4 9 |
02 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Введя |
|
оба |
|
равенства (7.32) |
|
в |
квадрат |
и складывая, |
|||||||||||||||||||||||||||||||||||
имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u02 |
|
u12 |
|
a02 , |
|
|
|
|
|
|
a0 |
(u02 |
|
u12 )1 2 . |
|
|
|
|
|
|||||||||||||||||||||
Из этих же равенств можно найти и параметр |
0 : |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
0 = |
|
arcsin |
|
|
|
|
|
u1 |
|
|
|
|
|
|
|
|
|
|
|
arccos |
|
|
|
u0 |
|
|
|
|
. |
||||||||||||||
|
|
|
2 |
u |
2 1/ 2 |
|
|
|
u |
|
2 |
u |
2 1/ 2 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||
Возведя в квадрат равенства (7.33) и сложив их, получим |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
|
3 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||
|
|
cos |
3 |
|
|
|
0 |
|
|
|
|
sin |
3 |
|
0 |
|
|
|
|
|
|
|
0 |
2 |
|
||||||||||||||||||
a1 |
|
a0 |
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
0sin 3 |
|
|
|
|
, |
||||||||||||||||||
4 |
(9 |
|
|
2 |
|
|
1) |
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
9 |
|
2 |
1 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||||||||||||||||||
а также |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
arccos |
|
|
|
|
|
|
a0 cos |
0 |
|
|
. |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
4(9 |
2 |
|
|
|
1) a |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, все постоянные выражены через две |
|||||||||||||||||||||||||||||||||||||||||||
заданные |
u0 |
|
и |
u1 . |
Преобразуем |
|
выражение |
для решения |
|||||||||||||||||||||||||||||||||||
уравнения Дюффинга, сложив два первых члена в (7.31). Используя известную тригонометрическую формулу, имеем
a |
0 |
cos( |
0 |
) |
a cos( |
0 |
) a cos( |
0 |
), |
|
|
0 |
1 |
1 |
|
246

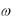


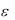

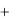
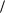
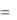 , (7.35)
, (7.35)