
3447
.pdf
при x min(Ra , Rb ) . Последняя сумма в выражении для
коэффициента |
Cn |
берется |
по |
возможным |
|
целым |
|
неотрицательным решениям уравнения k |
m |
n при заданном |
|||||
индексе n . |
|
|
|
|
|
|
|
В случае |
произведения N |
рядов |
можно получить по |
||||
индукции выражение |
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
a( j) |
xk ( j) |
xn |
|
a(1) |
... a(N ) |
, |
(6.12) |
k ( j) |
|
|
|
k (1) |
k (N ) |
|
|
j 1 k ( j) 0 |
|
n 0 k (1) ... |
k (n) n |
|
|
|
|
где внутренняя сумма в правой части берется по целым
неотрицательным решениям уравнения k1 |
k2 |
... |
kn n , а |
||||||||||||
радиус |
сходимости |
ряда |
в |
правой |
части |
равенства |
|||||||||
|
R |
min(R1R2 ,..., Rn ) .Сумма же ряда, равного произведению N |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
рядов, будет равна произведению сумм: A(x) |
|
Aj (x). |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
1 |
|
|
|
2. Деление степенных рядов. |
|
|
|
|
|||||||||
|
|
Если |
Ra |
|
0 , Rb |
0 и |
b0 |
0 , то при достаточно малых |
|||||||
значениях |
x |
|
справедливо следующее разложение в степенной |
||||||||||||
ряд частного: |
|
|
|
|
|
|
|
|
|
|
|||||
|
a |
a x ... |
a |
n |
xn ... |
|
|
... c xn |
|
|
|
||||
|
0 |
1 |
|
|
|
|
|
|
c |
c x |
... |
, |
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
b |
b x ... |
b xn ... |
0 |
1 |
n |
|
|
|
||||||
|
|
|
|
|
|
|
|||||||||
0 |
1 |
|
|
|
n |
|
|
|
|
|
|
|
|
||
коэффициенты |
|
cn которого можно найти |
по рекуррентным |
||||||||||||
формулам, полученным в результате умножения степенных рядов
a xn |
b xn |
c xn . |
n |
n |
n |
n 0 |
n 0 |
n 0 |
Используя формулы (6.10) и приравняв коэффициенты при одинаковых степенях x в правой и левой частях равенства, получим
220

a |
n |
xn |
xn |
|
c b , |
|
|
|
|
|
|
|
|
k |
m |
|
|
|
|
n 0 |
|
n 0 |
k m |
n |
|
|
|
|
|
a0 |
c0b0 , |
a1 |
c1b0 |
c0b1 , |
|
|
(6.13) |
||
|
|
|
|
|
|
|
n |
|
|
a2 |
c2b0 |
c1b1 |
c0b2 ,..., |
an |
cn |
k bk ,... . |
|||
|
|
|
|
|
|
k |
0 |
|
|
Из |
|
формул |
(6.13) |
видно, |
что |
коэффициенты |
|||
cn (n |
0,1,...) |
последовательно |
находятся |
из цепочки |
|||||
уравнений при условии |
b0 |
0 . |
|
|
|
||||
3. Обратный элемент для сходящегося степенного ряда.
На основе приведенных результатов по делению
степенных |
рядов |
можно |
ввести |
обратный |
ряд для |
ряда |
|||||
A(x) |
a |
n |
xn , |
a |
0 . По определению, ряд |
T (x) |
t |
n |
xn |
||
|
|
|
0 |
|
|
|
|
|
|
||
n |
0 |
|
|
|
|
|
|
n 0 |
|
|
|
называется |
|
обратным для |
ряда |
A(x) , если |
T(x)A(x) 1. |
||||||
Справедливо утверждение: если радиус сходимости ряда |
A(x) |
||||||||||
отличен от нуля, то обратный ряд T (x) имеет не равный нулю
радиус сходимости.
Из формул (6.13) как частный случай получаются
уравнения для |
определения |
коэффициентов tn ряда T (x) . |
|||
Выполняя умножение, имеем |
|
|
|
||
|
1 T (x) A(x) |
|
xn |
tk am . |
|
|
|
|
n 0 |
k m |
n |
Отсюда, используя формулы (7.13), получаем |
|||||
1 t0 a0 , |
0 |
t1a0 t0 a1, |
0 |
t2 a0 |
t1a1 t0 a2 ,..., |
n |
|
|
|
|
|
n,0 |
tn |
k ak ,..., |
|
|
(6.14) |
k 0 |
|
|
|
|
|
221

где символ Кронекера |
n,e |
1 при n e , |
n,e |
0 при |
n e . |
|
|
|
|
Из рекуррентной системы (6.14) последовательно находятся коэффициенты ряда T (x) :
t |
a 1, |
t |
a a 2 |
, t |
2 |
a2a 3 |
a a 2 |
,... . |
|||
0 |
0 |
1 |
1 |
0 |
|
1 |
0 |
2 |
0 |
|
|
4. Подстановка ряда в ряд.
Пусть функция y A(x) в промежутке ( R, R) является
суммой степенного ряда an xn , а функция B( y) является
|
n |
0 |
|
|
|
|
|
|
суммой степенного ряда в промежутке ( |
, ) |
|
|
|
|
|
||
B( y) b |
b y ... |
b yn ... |
b yn . |
(6.15) |
|
|||
0 |
1 |
n |
n |
|
|
|
|
|
|
|
n |
0 |
|
|
|
|
|
|
|
A(0) |
|
|
||||
Справедливо утверждение: при условии |
a0 |
|
|
, |
||||
сложная функция B(A(x)) в окрестности точки x |
0 является |
|||||||
суммой степенного ряда, полученного подстановкой в (6.15)
вместо y ряда |
A(x) , возведения в соответствующие степени и |
||||||
объединения затем подобных членов. |
|
|
|
|
|
||
Используя частный случай формулы (6.12) при |
a( j) |
a |
, |
||||
|
|
|
|
|
k |
k |
|
получим выражения для композиции рядов |
B( y) и A(x) |
|
|
||||
B( A(x)) |
xm |
b |
a |
...a |
, (6.16) |
|
|
|
|
n |
k (1) |
k (n) |
|
|
|
|
m 0 |
n 0 k (1) ... k (n) m |
|
|
|
|
|
где последняя сумма в правой части равенства (6.16) берется по целым неотрицательным решениям уравнения k1 ... kn m .
В развернутом виде формула (6.16) выглядит так
(A(x)) |
(b |
b a |
b a2 ... |
b an |
...) |
||||
|
|
0 |
1 |
0 |
2 |
0 |
|
n 0 |
|
x(b a |
|
2b a a |
... |
nb a an 1 |
...) |
||||
1 1 |
|
2 1 |
0 |
|
|
n 1 |
0 |
|
|
x2 (b a |
b (a2 |
2a a ) |
...) ... . |
||||||
|
1 |
2 |
2 |
1 |
|
2 |
0 |
|
|
5. Обращение степенного ряда.
222

Пусть необходимо найти |
x |
из уравнения y |
A(x) , где |
|||
функция A(x) задана в виде степенного ряда |
|
|||||
A(x) |
a |
n |
xn , |
|
a 0 . |
(6.17) |
|
|
|
|
0 |
|
|
|
n 1 |
|
|
|
|
|
Обратную функцию для |
функции y A(x) |
обозначим |
||||
x B( y) . Поскольку функция |
y |
A(x) задана не в замкнутом |
||||
виде, а в виде ряда, то и обратную функцию возможно построить лишь в виде ряда
|
|
|
|
|
x |
b yn . |
|
|
|
|
|
|
(6.18) |
|
|||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
Так мы приходим к задаче об обращении степенных |
||||||||||||||||
рядов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Справедливо утверждение. |
Пусть |
A(x) степенной ряд, |
||||||||||||||
такой, что A(0) |
0 , |
a1 |
0 . B( y) - |
ряд обратный ряду |
A(x) |
||||||||||||
относительно композиции, т.е. степенной |
ряд, |
такой, |
что |
||||||||||||||
B( y) |
0 и A(B( y)) |
y . Если радиус сходимости A(x) отличен |
|||||||||||||||
от нуля, то это же справедливо для ряда B( y) . |
|
|
|
|
|
|
|||||||||||
|
Получим |
соотношение, |
|
связывающие |
|
искомые |
|||||||||||
коэффициенты bn |
с заданными величинами an . Подставим x |
||||||||||||||||
из (6.18) в ряд (6.17) и воспользуемся (6.16). Получим |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
y |
a xn |
a |
|
b |
ym |
a |
ym |
|
|
|
|
b |
|
...b |
. |
||
|
n |
n |
|
m |
|
n |
|
|
|
|
|
k (1) |
|
k(n) |
|
||
n 1 |
n 1 |
m 1 |
|
n 1 |
m |
n |
k(1) ... |
k(n) |
m |
|
|
|
|
||||
|
Изменив порядок суммирования в двух первых суммах, |
||||||||||||||||
запишем окончательно |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
y |
yn |
n |
a |
|
|
b |
|
...b |
|
. |
|
|
(6.19) |
||
|
|
|
|
|
m |
|
|
k (1) |
k (m) |
|
|
|
|
|
|
||
|
|
n 1 |
m 1 |
|
k (1) ... k (m) |
n |
|
|
|
|
|
|
|
|
|
||
|
Приравнивая в (6.19) коэффициенты при одинаковых |
||||||||||||||||
степенях |
y в правой |
и |
левой |
частях |
равенства, |
получим |
|||||||||||
223

рекуррентную систему уравнений, определяющую коэффициенты bn ряда (6.18):
a b |
|
1, |
|
a b |
a b2 |
|
0, |
|
|
|
|
|
|
|
|
|
|
(6.20) |
|||||||
1 1 |
|
|
|
|
1 2 |
|
2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a b |
|
a |
|
b b |
|
a b3 |
0, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 3 |
2 |
|
|
k |
e |
3 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
k |
e |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a b a |
|
b b a |
|
|
|
|
|
|
b b b |
|
a b4 |
|
0, |
|
|
|
|||||||||
1 4 |
2 |
|
|
k e |
3 |
|
|
|
|
|
|
k e m |
|
|
4 1 |
|
|
|
|
|
|
||||
|
|
k |
e |
4 |
|
|
k |
e m |
4 |
|
|
|
|
|
|
|
|
|
|
||||||
………………………………………………………………… |
|
||||||||||||||||||||||||
a b |
a |
b b |
a |
|
|
|
|
b b b ... |
a |
(n |
1)bn |
2b |
a bn |
0 . |
|||||||||||
1 n |
|
2 |
|
|
k e |
3 |
|
|
|
|
k e m |
n 1 |
|
|
1 |
2 |
|
n 1 |
|
||||||
|
|
k e |
n |
|
|
k e |
m |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Отсюда последовательно находятся коэффициенты bn : |
|
||||||||||||||||||||||||
|
b |
a |
1, |
|
b |
|
a |
3a , |
|
|
b |
|
a 4a |
|
2a |
5a2 ,... . |
|
||||||||
|
1 |
1 |
|
2 |
|
|
1 |
2 |
3 |
|
|
1 |
3 |
|
1 |
2 |
|
||||||||
|
Пример. Зная разложение в ряд функции y |
sin x , найти |
|||||||||||||||||||||||
разложение в ряд функции x |
|
arcsin y . |
|
|
|
|
|
|
|
||||||||||||||||
|
Решение. Считаем известным разложение в степенной |
||||||||||||||||||||||||
ряд функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
x3 |
|
x5 |
|
|
1)n 1 |
|
x2n 1 |
|
|||||||
|
|
|
|
y |
sin x |
|
x |
|
|
|
|
|
|
|
... |
( |
|
|
|
... . |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
6 |
|
|
120 |
|
|
|
|
|
(2n |
1)! |
|
||||
Ищем разложение обратной функции в виде |
|
|
|
|
|
|
|||||||||||||||||||
x |
arcsin y |
b y |
b y3 |
|
b y5 ... . |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
1 |
|
3 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Записанный ряд содержит только нечетные степени |
y , |
|||||||||||||||||||||||
т.к. |
функция y |
sin x |
нечетная и |
потому |
обратная к |
ней |
|||||||||||||||||||
функция также нечетная. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Из |
|
|
формулы |
|
|
|
(6.19) |
|
|
|
имеем: |
|||||||||||||
|
a b 1, b 1, |
|
b |
|
|
a 2a2 |
1 |
, |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
1 1 |
|
|
1 |
|
3 |
|
3 |
2 |
6 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
|
1 |
5 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
b5 |
|
|
b1 b3 |
|
b1 |
|
|
|
,... . |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 |
120 |
|
40 |
|
|
|
|
|
|
|
|
|
|
||||||||||
224

Получаем x |
arcsin y |
y |
|
y3 |
|
|
3 |
y5 |
|
|
5 |
x7 ... . |
|
|
6 |
|
40 |
|
12 |
|
|||||||||
|
|
|
|
|
|
|
|
|||||||
6.6. Разложение функций в степенные ряды |
|
|||||||||||||
Определение. |
Говорят, |
что |
функция |
f (x) |
||||||||||
разлагается |
в степенной |
|
ряд |
(6.4) |
или |
(6.5) на интервале |
||||||||
( R, R) R |
0 , если на этом интервале данный степенной ряд |
|||||||||||||
сходится и его сумма равна |
f (x) , т.е. |
|
|
|
|
|||||||||
f (x) |
a (x |
x |
)k |
при x |
x |
|
из ( R, R) . |
(6.21) |
||||||
|
k |
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Основные теоремы о разложении функций в степенные ряды.
Теорема (одна и та же функция не может иметь двух разных разложений) степенной ряд (6.21), сходящийся на ( R, R) R 0 , является рядом Тейлора для своей суммы, т.е. его коэффициенты находятся по формулам Тейлора
ak |
f k (x0 ) |
, |
k 0,1,2,..., |
(6.22) |
|
k! |
|||||
|
|
|
|
а следовательно, коэффициенты ряда (6.22) определяются по его сумме однозначно.
Итак, если функцию y 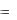 f (x) в окрестности точки x0
f (x) в окрестности точки x0
можно разложить в сходящийся к ней ряд, то он является для этой функции рядом Тейлора
|
f ' (x ) |
|
f ''(x |
) |
(x x )2 ... |
f (x) f (x ) |
0 |
(x x ) |
0 |
|
|
|
|
|
|||
0 |
1! |
0 |
2! |
|
0 |
|
|
|
|
|
f (n) (x |
) |
|
(x x )n |
|
|
|
|
|
|
|||
... |
|
0 |
|
... . |
|
|
|
(6.23) |
|||||
|
|
|
|
|
|
|
|
||||||
|
n! |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В случае если |
x0 |
0 , полученный ряд называется рядом |
|||||||||||
Маклорена |
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
f (0) |
|
|
f |
'(0) |
x ... |
|
f (n) (0) |
x |
n |
... . |
(6.24) |
|
|
|
|
|
1! |
|
n! |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
225

Обратное утверждение, вообще говоря, не справедливо. Если функция f (x) бесконечно дифференцируема и для нее
формально построен ряд Тейлора (6.23) или Маклорена (6.24), то он не всегда сходится к этой функции. Следующая теорема устанавливает условия разложимости функции в степенной ряд.
Теорема. Для того, чтобы функцию f (x) можно было разложить в степенной ряд (6.21) с радиусом сходимости R 0 , необходимо и достаточно, чтобы f (x) имела на этом
интервале производные всех порядков и чтобы остаточный член в формуле Тейлора
|
|
|
f (n) (x ) |
(x x )n |
|
f (x) f (x ) |
f '(x )(x |
x ) ... |
0 |
R , |
|
|
|||||
0 |
0 |
0 |
n! |
0 |
n |
|
|
|
|
|
|
|
(x |
x )n 1 |
f (n 1) (x |
|
|
|
|
|
|
где |
R |
|
0 |
(x |
x |
)), 0 |
|
1, |
||
|
|
|
||||||||
|
n |
(n |
1)! |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
стремился к |
нулю |
при |
n |
для |
всех |
x |
из интервала |
|||
сходимости. |
|
|
|
|
|
|
|
|
||
|
На практике |
при |
решении |
вопроса |
о |
возможности |
||||
разложения функции в ряд Тейлора или Маклорена удобнее использовать достаточные условия, сформулированные ниже.
Теорема. Для того чтобы функцию f (x) можно было разложить в степенной ряд (6.21), достаточно, чтобы f (x) имела на интервале (x0 R, x0 R) производные всех порядков
и чтобы |
существовала такая |
постоянная M , что |
||
|
f (n) (x) |
|
M при n 0,1,2,... и всех x |
из этого интервала, т.е. |
|
|
|||
чтобы производные всех порядков были равномерно ограничены в совокупности на этом интервале.
Определение. Функция f (x) , разлагающаяся в ряд
Тейлора, называется аналитической функцией.
Ряды Маклорена некоторых элементарных функций
226
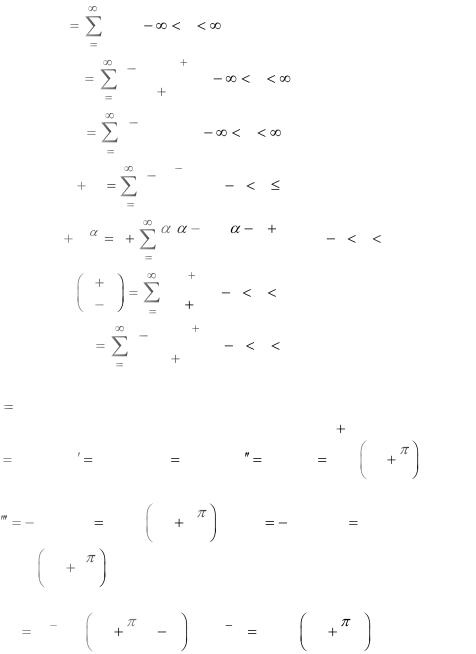
1. |
ex |
|
xn |
|
, |
x |
, |
|
||
0 n! |
|
|||||||||
|
n |
|
|
|
|
|
||||
|
|
( |
|
1)n x2n 1 |
|
|
||||
2. |
sin x |
|
|
|
|
|
|
, |
x |
, |
n 0 |
|
(2n 1)! |
||||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
( |
1)n x2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
3. |
cos x |
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
x |
|
, |
|
|
|
|
|
|
|
|
||||||
|
n 0 |
(2n)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
( |
1)n 1 xn |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
4. |
ln(1 |
|
|
x) |
|
|
|
|
|
|
|
|
|
|
|
, |
1 |
x |
1, |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
5. |
(1 |
|
x) |
1 |
|
|
( |
|
|
1)...( |
|
n |
1) |
|
x |
n |
, |
1 |
x 1. |
|
|
|||||||||||||
|
|
n |
0 |
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
1 |
x |
|
|
|
|
x2n 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
6. |
|
|
|
ln |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
1 |
x |
1. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2 |
|
|
1 |
x |
|
n |
0 2n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
( 1)n x |
2n 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
7. |
arctgx |
|
|
|
|
|
|
|
|
|
|
|
|
, |
1 |
x |
1. |
|
|
|
|
|
|
|||||||||||
|
n 0 |
|
|
2n |
1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Пример. |
Разложить |
в |
|
ряд |
по |
степеням |
n |
функцию |
||||||||||||||||||||||||||
y |
sin2 x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Решение. Продифференцировать функцию n 1 раз: |
|
|
||||||||||||||||||||||||||||||||
y |
sin2 x, y |
|
|
|
2sin x cos x |
sin 2x, |
y |
2 cos 2x |
2sin |
2x |
|
, |
|||||||||||||||||||||||
|
|
|
2 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
22 sin 2x |
22 sin |
2x |
2 |
|
|
, |
y(4) |
23 cos 2x |
|
|
|
|||||||||||||||||||||||
2 |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= 23 sin |
2x |
|
3 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
………………………………………………………………………
y(n) 2n 1 sin 2x |
|
(n 1) , y(n 1) |
2n sin 2x |
|
n . . |
|
2 |
2 |
|||||
|
|
|
|
227

|
Найдем |
значение |
функции |
|
и производных до n го |
|||||||||||||||||||||||||||
порядка в точке |
x |
|
0 , |
а значение |
y(n 1) |
в промежуточной |
||||||||||||||||||||||||||
точке для определения остатка Rn . Получаем: |
|
|
|
|||||||||||||||||||||||||||||
y(0) 0, |
y (0) |
0, |
y (0) |
|
2, |
|
y |
(0) |
0, |
y(4) (0) |
|
23 ,..., |
||||||||||||||||||||
y(n) (0) |
2n 1 sin |
|
(n |
1) |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
при |
|
|
|
|
n |
2k 1, |
||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(n) (0) |
( 1)k 22k |
1 |
при |
|
n |
|
2k 2. |
|
|
|
|
|
|
|
|
|||||||||||||||||
Найдем остаточный член |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
R |
|
2n sin(2t |
|
n / 2) |
x |
n 1 |
|
1 (2x)n 1 |
sin(2t |
|
n / 2), |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
n |
|
|
(n |
1)! |
|
|
|
|
|
|
|
|
|
|
|
2 (2n |
1)! |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
где |
t |
x , |
0 |
|
|
|
1. |
|
Поскольку |
sin |
2t |
|
n |
- |
величина |
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
2 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ограниченная и при любом x |
имеет место равенство |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
lim |
|
|
(2x)n 1 |
|
0, |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
(2n |
|
1)! |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
то |
lim R |
0 . |
Следовательно, |
функцию |
y sin2 x |
можно |
||||||||||||||||||||||||||
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
записать как сумму ряда Маклорена |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
sin2 x |
|
2 |
|
|
x2 |
|
|
23 |
|
x4 |
|
25 |
x6 ... . |
|
|
|
||||||||||||
|
|
|
|
2! |
|
4! |
|
6! |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
6.7. Обобщения степенных рядов – интегро – степенные ряды и ряды Вольтерра
Классические степенные ряды, изученные в этой главе, являются эффективным инструментом для различного рода уравнений, вычисления интегралов, исследования функций и моделирования некоторых физических и технических систем.
В высших разделах математического анализа используются ряды более общего типа. В течении нескольких последних десятилетий обобщения степенных рядов применялись при моделировании процессов в электрических
228

цепях, в функциональной электронике, в механике полимерных и композитных материалов и в приложениях к исследованию устойчивости форм равновесия.
Определение. Пусть Kn (t, t1,..., tn ) - функция,
непрерывная |
по |
совокупности аргументов |
|
при t, t1,..., tn |
из |
|||||||||
[a,b] , |
|
0 , |
1,..., |
|
n |
- неотрицательные |
|
целые |
|
числа |
и |
|||
0 |
1 |
... |
n |
|
m . Выражения |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
b |
b |
|
|
|
|
|
|
|
|
|
|
|
u |
(0) (t) ... K |
n |
(t, t ,..., t |
n |
)u (1) |
(t )...u (n) (t |
n |
)dt ...dt |
n |
(6.25) |
||||
|
|
|
|
1 |
|
|
1 |
1 |
|
|
||||
|
|
a |
a |
|
|
|
|
|
|
|
|
|
|
|
называется интегро – степенным членом степени m относительно u(t) и обозначается Wm (t, u[ ] ) , где (i) i .
Каждый интегро – степенной член (6.25) соответствует определенному набору чисел 0 , 1,..., n , т.е. определенному
решению |
|
уравнения в целых неотрицательных числах |
|
0 1 |
... |
n |
m |
|
|
||
Определение. Сумма всех интегро – степенных членов данной степени m называется интегро – степенной формой и обозначается Wm (t, u) , т.е.
w (t,u) |
W (t,u[ ]) |
m |
m |
(0) ... |
(n) m |
Выражение
Wm (t, u) |
(6.26) |
m 0
называется интегро – степенным рядом.
Введем понятие сходимости ряда, часто применяемое в приложениях. Интегро – степенной ряд (6.26) называется регулярно сходящимся, если сходится числовой ряд
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
n |
|
|
|
|
|
|
w0 |
w1 |
u |
wn |
u |
..., |
|||||||
|
|
|
|
|
|
||||||||||||
где u max |
u(t) |
, wn |
max wn (t,1). |
|
|||||||||||||
229
