
3447
.pdf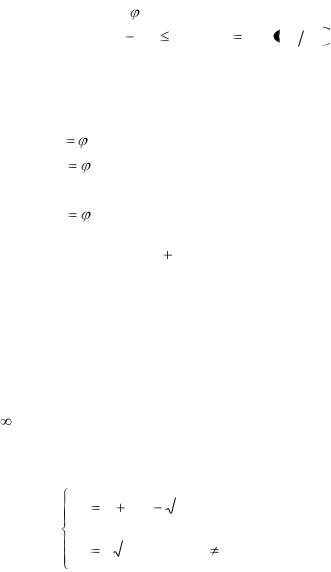
дифференцируемо |
(все |
k (x) |
имеют |
непрерывные |
||
|
x0 |
|
h, где h |
|
||
производные) в интервале |
x |
|
min a,b M . |
|||
3. Понятие общего, частного и особого решений.
В упрощенной формулировке общее решение системы
(5.1) определяется |
как семейство решений этой системы, |
||
зависящее от n произвольных параметров C1, C2 , , Cn |
|
||
y1 |
1(x, C1, , Cn ), |
|
|
y2 2 (x, C1, , Cn ), |
(5.8) |
||
|
|||
|
|||
yn |
n (x, C1, , Cn ). |
|
|
Геометрически общее решение есть семейство |
|||
интегральных кривых в |
(n 1) -мерном |
пространстве |
|
x, y1, , yn , зависящее |
от |
n параметров |
C1, C2 , , Cn , |
причем уравнения этого семейства линий разрешены относительно y1, , yn .
Частное решение системы – это такое решение, которое состоит из точек единственности решения задачи Коши.
Решение, получаемое из общего решения при определенных числовых значениях параметров C1, C2 , , Cn ,
включая  , является частным решением.
, является частным решением.
Особым решением называется такое, в каждой точке которого нарушается единственность решения задачи Коши.
Пример. Найти решение системы
dy |
|
2 |
|
|
|
|
|||
x |
y |
|
z , |
||||||
dx |
|
x |
|||||||
|
|
|
(5.9) |
||||||
dz |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
2 |
z , |
|
где x 0. |
||||||
|
|
||||||||
dx |
|
||||||||
|
|
|
|
|
|
|
|
||
Решение. Заданная система, представляет собой совокупность зацепляющихся уравнений – одно из них можно решить независимо от другого. Интегрируем второе уравнение, разделяя переменные
160
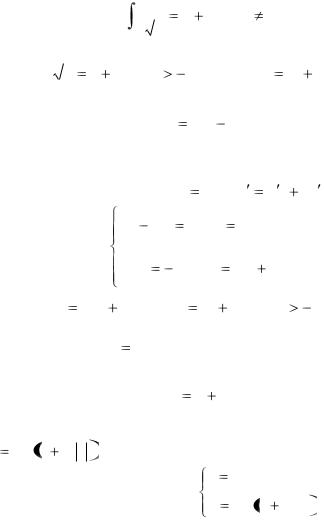
|
|
|
dz |
x C1, z |
0. |
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 z |
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||
Откуда |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
C ) , |
или |
|
C )2. |
|||||
|
z x C |
(x |
z (x |
||||||||||
1 |
|
|
|
|
|
1 |
|
|
1 |
||||
Подставим найденную функцию в первое уравнение |
|||||||||||||
|
|
|
|
|
dy |
|
2 |
y |
C . |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
dx |
|
x |
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
Полученное |
уравнение |
является |
линейным |
||||||||||
дифференциальным уравнением 1-го порядка. Его решение
найдем методом Бернулли: |
y |
uv, |
|
y |
u v |
uv , |
|||||||
|
dv |
|
2 |
v |
0, |
v |
|
x2 , |
|
|
|||
|
|
|
|
|
|
|
|||||||
|
dx |
|
x |
|
|
|
|
|
|
|
|||
|
du |
|
v |
C1, |
u |
|
C1 |
|
C2 |
, |
|||
|
dx |
|
x |
||||||||||
|
|
|
|
|
|
|
|
|
|||||
откуда: y C x |
C |
2 |
x2 , |
z |
(x |
C )2 |
(x |
C ) - общее |
|||||
1 |
|
|
|
|
|
|
1 |
|
|
1 |
|||
решение системы. Второе уравнение системы (5.9) имеет
особое решение |
z 0 . Подставим |
его |
в первое |
уравнение, |
|||||
получим |
|
|
|
|
|
|
|
|
|
|
|
dy |
|
x |
2 |
|
y. |
|
|
|
|
dx |
x |
|
|
||||
|
|
|
|
|
|
||||
Решая это |
уравнение |
методом |
Бернулли, |
получим |
|||||
y x 2 C ln x . Итак, система (5.9) помимо общего решения
z |
0, |
|
|
имеет еще семейство решений |
x2 C ln |
|
|
y |
x |
. |
5.3. Интегрирование системы дифференциальных уравнений, сведением к одному уравнению n – го порядка
В предыдущих разделах V–й главы рассматривались примеры нахождения решений систем уравнений. Однако используемые там приемы интегрирования не были систематическими, а носили скорее характер ”ad hoc”. В этом
161

разделе будет рассмотрен один из основных методов интегрирования системы дифференциальных уравнений.
Суть используемого здесь метода заключается в следующем: из уравнений системы и из уравнений, получающихся дифференцированием уравнений системы,
исключаются |
все искомые функции, кроме |
одной. |
Для |
||
определения |
этой |
функции |
получают |
|
одно |
дифференциальное уравнение n – го порядка (в случае системы из n уравнений). Из полученного уравнения находится одна неизвестная функция, а остальные искомые функции находятся из исходных уравнений и уравнений, получившихся в результате их дифференцирования.
1*. Общий случай нормальной системы.
Рассмотрим схему приведения системы к одному дифференциальному уравнению n – го порядка в случае системы вида (5.1):
yk |
f k (x, y1, y2 , , yn ) (k |
1,2, , n) . |
(5.10) |
|
Метод исключения неизвестных реализуется в |
||||
предположении, что все функции |
f k (k |
1,2, , n) |
имеют |
|
непрерывные |
частные производные |
до (n |
1) - го |
порядка |
включительно по всем аргументам x, y1, y2 , , yn .
Дифференцируя, например, первое из уравнений (5.10) последовательно (n 1) раз и подставляя на каждом шаге
вместо производных yk (k 1,2, , n) их значения, взятые из
правых частей уравнений (5.10), мы получим следующие уравнения:
y |
|
|
|
f1 |
|
|
f1 |
y |
f1 |
|
y |
n |
|
f1 |
|
|
|
f1 |
f |
1 |
|
|
|
f1 |
f |
n |
, |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1 |
|
|
|
|
|
1 |
|
yn |
|
|
|
|
|
y1 |
|
|
yn |
|
|
|
||||||||||||
|
|
|
|
x |
|
|
y1 |
|
|
x |
|
|
|
|
|
|
|
|
||||||||||||||
или |
y1 |
|
F2 (x, y1, y2 , , yn ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
y |
|
F2 |
|
|
|
F2 |
y |
|
F2 |
y |
n |
|
F2 |
|
|
F2 |
f |
1 |
|
|
Fn |
f |
n |
, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1 |
|
|
|
|
|
1 |
|
yn |
|
|
|
|
|
y1 |
|
|
|
yn |
|
|
|
|||||||||||
|
|
|
|
x |
|
|
y1 |
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||||||||
или |
y1 |
|
F3 (x, y1, y2 , , yn ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
162

y1(m)
или
или
|
Fm 1 |
|
n |
Fm 1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
f |
, |
|
(m 2,3, , n 1) |
||||||||||||
|
|
|
|
|
|
|
||||||||||||
|
x |
|
|
|
yl |
|
|
|
l |
|
|
|
|
|
|
|
||
|
|
|
l 1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(m) |
F (x, y , y |
2 |
, , y |
n |
) (m 2, , n 1) |
|||||||||||||
1 |
|
m |
|
1 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
y (n) |
|
|
|
Fn 1 |
|
|
n |
Fn 1 f |
|
|||||
|
|
|
|
|
|
|
|
|
, |
|||||||||
|
|
|
|
1 |
|
|
|
|
|
|
x |
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l 1 |
yl |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(n) |
F (x, y , , y |
n |
) . |
|
|
|
|
|
|
|||||||||
1 |
n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
При получении этих уравнений использовали правило дифференцирования сложной функции многих переменных: если
u |
f (x, y1, , yn ) , где y1 g1 (x) , |
y2 |
g2 (x) , , |
yn |
g n (x) , |
|||
функция |
u |
f (x, y1, , yn ) |
дифференцируема |
в |
точке |
|||
(x, y1 , , yn ) , а функции gk (x) |
(k |
1,2, , n) имеют производную |
||||||
в |
точке |
x , |
то производная |
по |
x |
от сложной |
функции |
|
u F (x)  f (x, g1 (x), , g n (x)) вычисляется по формуле
f (x, g1 (x), , g n (x)) вычисляется по формуле
|
dF |
|
|
|
|
f |
|
|
|
f |
g (x) |
|
f |
g |
|
(x) . |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
yn |
|
|||
|
dx |
|
|
|
|
x |
|
|
|
y1 |
|
|
|
|||||
Таким образом, получена система (n |
1) уравнений |
|||||||||||||||||
|
|
|
dy1 |
|
f1 |
(x, y1, , yn ), |
|
|
|
|
|
|||||||
|
|
|
dx |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
d 2 y |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
|
|
|
F2 (x, y1, , yn ), |
|
|
|||||||||
|
|
|
dx2 |
|
|
|
(5.11) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
||||||||||||||
|
|
|
d n 1 y |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
Fn 1 (x, y1, , yn ) |
|
|
|||||||||||
|
|
|
dxn 1 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
и еще одно уравнение |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
d n y |
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
Fn (x, y1, , yn ). |
|
(5.12) |
||||||||||
|
|
|
|
dxn |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Дальнейшее продвижение по намеченной схеме заключается в исключении из уравнения (5.12) функций
163

y1, y2 , , yn . Для этого следует использовать систему (5.11), рассматривая ее как систему алгебраических уравнений относительно неизвестных y2 , , yn . Требуем, чтобы эта
система была разрешима относительно указанных неизвестных. Из математического анализа известно, что для разрешимости такой системы уравнений требуется выполнение условия
|
|
f1 |
|
f1 |
|
|
|
|
f1 |
|
|
|
|
|||
|
|
y2 |
y3 |
|
|
|
yn |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
F2 |
|
F2 |
|
|
|
|
F2 |
|
|
|
|
|||
|
|
y2 |
y3 |
|
|
|
yn |
0. |
|
(5.13) |
||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Fn 1 |
|
|
Fn 1 |
|
|
|
Fn 1 |
|
|
|
||||
|
|
y2 |
y3 |
|
|
|
y3 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||
Предполагая, что условие (5.13) выполняется, выразим |
||||||||||||||||
из уравнений (5.11) |
y |
2 |
, , y |
n |
через x, y |
y , , y(n 1) и |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
1, |
1 |
1 |
|||
подставим эти выражения в уравнение (5.12). В результате для
функции y1 получим дифференциальное уравнение |
n – го |
|||
порядка: |
|
|
|
|
y(n) |
f (x, y |
y , , y(n 1) ). |
(5.14) |
|
1 |
1, |
1 |
1 |
|
Решив уравнение (5.14) получим функцию y1(x) , а затем ее производные y1, , y1(n 1) . Это позволит найти остальные неизвестные y2 , , yn , поскольку они выражаются через
x, y1, y1, , y1(n 1) из системы (5.11).
Можно показать (мы на этом не останавливаемся), что при сделанных предположениях, решение y1(x) , найденное из (5.14) а также функции y2 , , yn , найденные из (5.11), в
совокупности будут являться решением системы уравнений (5.10). И наоборот – решение системы (5.10) будет являться решением уравнения (5.14) и системы (5.11).
164

Пример. Решить систему уравнений
dy |
1 |
1 |
, |
|||
dx |
|
z |
||||
|
|
|
|
|
||
dz |
|
|
1 |
|
. |
|
|
|
|
|
|
||
dx |
|
y |
|
x |
||
Решение. Дифференцируя обе части первого уравнения, получим:
d 2 y |
1 |
|
dz |
. |
|
dx2 |
|
z 2 |
|
dx |
|
|
|
|
|||
Из уравнений системы имеем:
dz |
1 |
|
1 |
|
dy |
2 |
|
, |
|
1 . |
|||||
|
|
|
|
|
|
||
dx |
|
y x |
z 2 |
|
dx |
||
Подставим эти выражения в предыдущее уравнение и присоединим выражение для z , найденное из 1-го уравнения:
|
|
|
|
|
|
|
|
d 2 y |
|
1 |
|
|
|
|
dy |
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
, |
|
|
|
z |
|
|
|
|
|
. |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
dx2 |
|
|
|
y |
x |
dx |
|
|
|
1 |
|
dy |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Для решения уравнения 2-го порядка представим его в |
|||||||||||||||||||||||||||||||||||||||||||
виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
d |
|
|
dy |
1 |
|
|
|
|
|
dy |
1 |
|
|
|
|
|
|
|
|
dy |
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
dx dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
dx |
|
|
где |
|
|
dx |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
|
y x |
|
. |
||||||||||||||
|
|
|
|
dy |
|
1 |
|
|
|
|
|
y |
|
x |
|
|
|
y |
x |
dx |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Получим уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
dy |
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ln |
|
1 |
|
|
ln |
y |
x |
. |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
dy |
|
|
|
dx |
|
dx |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Отсюда |
1 C ( y |
x), |
|
C |
0. Преобразуем его к виду: |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
dx |
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
d
dx ( y x) C1 ( y x).
165

Интегрируя, имеем: y |
|
x C |
2 |
eC1x |
, |
C |
0, C |
2 |
|
, . |
|||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
Находим вторую неизвестную функцию: |
|
|
|
|
|
|
|||||||||||||
z |
|
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
|
dy |
|
|
C1 ( y x) |
|
|
|
C C |
|
eC1x |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
||
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, решение системы имеет вид:
y x C |
|
eC1x , |
z |
1 |
e C1x . |
2 |
|
||||
|
|
|
C1C2 |
||
|
|
|
|
||
2. Нормальная система линейных уравнений с |
|||||
постоянными коэффициентами. |
|
|
|
||
В случае линейной |
системы с постоянными |
||||
коэффициентами процедуру исключения неизвестных можно выполнить с большим изяществом. Идея реализуемого ниже метода та же, что и при исключении неизвестных из линейной системы алгебраических уравнений, решаемых методом Крамера. Покажем это на примере системы трех линейных
дифференциальных |
уравнений. Обобщение на случай n |
|||||||
уравнений производится автоматически. |
|
|||||||
|
Пусть |
|
задана |
нормальная |
система |
линейных |
||
дифференциальных |
уравнений |
с |
постоянными |
|||||
коэффициентами aij |
|
|
|
|
||||
|
|
dy1 |
|
a11 y1 |
a12 y2 |
a13 y3 |
f1 (x), |
|
|
|
dx |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
dy2 |
|
a21 y1 |
a22 y2 |
a23 y3 |
f 2 (x), |
(5.14) |
|
|
dx |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
dy3 |
|
a31 y1 |
a32 y2 |
a33 y3 |
f3 (x), |
|
|
|
dx |
|
|
||||
|
|
|
|
|
|
|
|
|
где |
f k (x) |
|
(k 1,2,3) - дважды непрерывно |
дифференци- |
||||
руемые функции, заданные на (a,b) . Запишем систему (5.14) в виде:
166
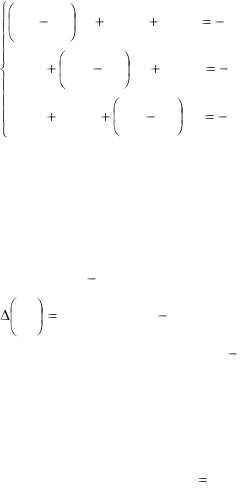
a11 |
d |
|
y1 |
a12 y2 |
a13 y3 |
f1 (x), |
|
|||
|
|
|
||||||||
|
|
|
||||||||
|
dx |
|
|
|
|
|
|
|
||
a21 y1 |
|
a22 |
d |
|
y2 |
a23 y3 |
f 2 (x), |
(5.15) |
||
|
|
|
||||||||
|
|
|
||||||||
|
|
|
|
dx |
|
|
|
|
||
a31 y1 |
a32 y2 |
|
a33 |
d |
y3 |
f3 (x). |
|
|||
|
|
|
||||||||
|
dx |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
Эта система формально аналогична системе линейных неоднородных алгебраических уравнений. Как и в методе Крамера введем главный определитель системы, который в нашем случае будет содержать элементы, зависящие от
оператора |
d |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
a11 |
d |
|
a12 |
|
a13 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
dx |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
a22 |
|
a22 |
|
|
d |
|
a23 |
. |
|
|
|
(5.16) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
dx |
|
|
dx |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
a31 |
|
|
a32 |
a33 |
d |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
dx |
|
|
|
|
|
|
|||||||||||||
Правило вычисления этого детерминанта такое же, как и |
||||||||||||||||||||||||
для определителя с |
числовыми |
|
элементами. |
|
Отличие |
|||||||||||||||||||
заключается в том, что при ”умножении” |
|
d |
d |
получается |
||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
dx dx |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
d d |
|
d 2 |
|
|
|
|
|
|
|
|
||||||
символ 2-ой |
производной |
|
|
|
|
|
|
|
. Таким |
образом |
||||||||||||||
|
dx dx |
dx2 |
||||||||||||||||||||||
введенный определитель содержит символы производной первого, второго и третьего порядков. Как и для обычного числового определителя для операторного определителя справедлива теорема разложения по элемента какого – либо ряда. Этим свойством мы сейчас и воспользуемся.
Для исключения функций y2 и y3 из уравнений (5.15) умножим обе части первого из них слева на A11 , второго
167
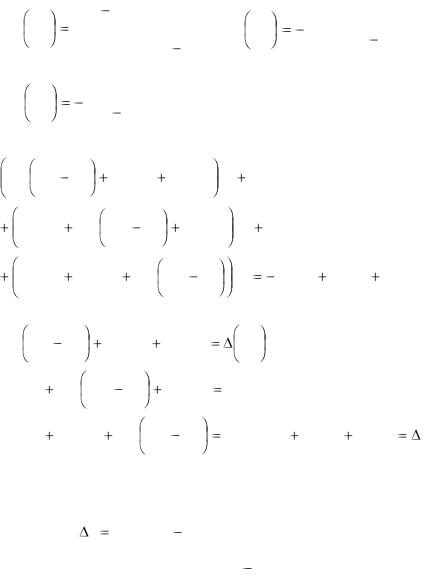
уравнения - на A21 |
и третьего – на A31 , где обозначили |
Aij - |
||||||||||||||||||
алгебраическое |
дополнение |
соответствующего |
элемента |
|||||||||||||||||
определителя (5.16) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
d |
|
a22 |
d |
a23 |
|
|
|
d |
|
a12 |
a13 |
|
|||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
A11 |
dx |
|
, |
A21 |
, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|||||||
dx |
|
|
a32 |
|
|
|
a33 |
d |
dx |
|
a32 |
a33 |
|
|||||||
|
|
|
|
|
|
|
|
|
dx |
|
||||||||||
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
||||
|
d |
|
|
a12 |
a13 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
A31 |
|
|
|
|
d |
|
|
, |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
a22 |
|
a23 |
|
|
|
|
|
|
|
|
|
|
||||
dx |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|||||||
затем сложим эти уравнения. Получим:
A11 a11 |
|
|
d |
|
A21a21 |
A31a31 |
y1 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
dx |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A11a12 |
|
|
A21 |
a22 |
d |
|
A31a32 y2 |
|
|
|
|
(5.17) |
|||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
dx |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A11a13 |
|
|
A21a23 A31 |
a33 |
|
|
|
d |
y3 |
|
|
( A11 f1 A21 f2 A31 f3 ). |
|||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
dx |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Поскольку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
A11 a11 |
|
d |
A21a21 |
A31a31 |
|
d |
|
, |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
dx |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
||||||
A11a12 |
A21 a22 |
|
d |
|
A31a32 |
0, |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
dx |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A11a13 A21a23 |
|
A31 |
a33 |
|
d |
0, A11 f1 A21 f 2 |
A31 f3 |
1, |
|||||||||||||
|
|
|
|
|
|||||||||||||||||
|
dx |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где введена функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
f1 |
|
a12 |
|
|
|
|
a13 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
f 2 |
a22 |
|
d |
a23 |
|
|
, |
(5.18) |
||||||
|
1 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
dx |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
f3 |
|
a32 |
|
|
|
|
a33 |
|
d |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
168

то уравнение (5.17) можно записать в виде:
|
d |
y1 |
1 . |
(5.19) |
|
|
|||
|
dx |
|||
|
|
|
|
|
Полученное уравнение |
для функции |
y1 является |
||
линейным неоднородным дифференциальным уравнением третьего порядка с постоянными коэффициентами. Интегрируя это уравнение одним из методов, изложенным в
главе 4, |
найдем |
функцию y1 . Функции y2 |
и y3 можно |
|||
определить из системы алгебраических уравнений |
||||||
a12 y2 |
a13 y3 |
y1 |
f1, |
|
||
(a12 a22 |
a13 a32 ) y2 |
(a12 a23 a13 a33 ) y3 |
(5.20) |
|||
|
d |
a11 y1 |
(a12 a21 a13 a31 ) y1 f1 a12 f 2 |
a13 f3. |
||
|
|
|
||||
|
dx |
|||||
|
|
|
|
|
||
Первое уравнение системы (5.20) есть первое уравнение в (5.14). Второе уравнение получается дифференцированием этого уравнения, с последующим исключением производных y2 и y3 , выражения для которых берутся из второго и
третьего уравнений системы (5.14).
При решении системы двух линейных уравнений с постоянными коэффициентами удобнее использовать метод исключения в виде, изложенном в п.1 этого параграфа.
Пример. Решить систему уравнений
|
|
|
|
|
|
|
|
dy |
3y 2z, |
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
dx |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dz |
2 y |
z. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
dx |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
|
Дифференцируем |
второе |
уравнение: |
|||||||
|
d 2 z |
2 |
dy |
|
dz |
. |
Подставим в это уравнение y |
из первого |
|||||
|
dx2 |
dx |
|
dx |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
уравнения и y - из второго: |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
y 3y 2z, y |
|
1 |
(z z). |
|
||
|
|
|
|
|
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
169
