Математическое моделирование в естественных науках

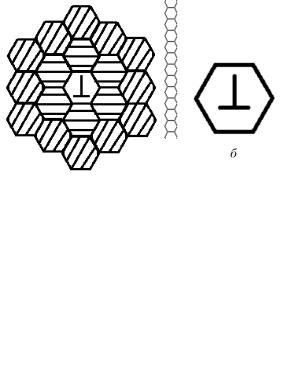
1.Поле моделирования представляет собой совокупность клеток, изображенных на рис. 2, а.

2.Клетка может находиться в одном из 7 состояний: 6 активных (в клетке находится дислокация одного из 6 направлений скольжения), 1 неактивном (пустая, свободная клетка). Неактивные клетки обозначаются белым цветом, активные– значком дислокации (рис. 2, б) ссоответствующим направлением скольжения.

3.Окрестностью ячейки являются два «слоя» клеток, окружающих рассматриваемую дислокацию (рис. 3).

Рис. 2. Поле моделирования (а), ячейка с дислокацией (б)

Рис. 3. Окрестность ячейки (горизонтальной штриховкой обозначены ячейки, входящие в 1-й «слой», наклонной штриховкой – во 2-й «слой»)

361

Если напряжение, действующее на текущую дислокацию, превышает или равно напряжению Пайерлса, то дислокация сдвигается в следующую свободную ячейку по направлению вектора Бюргера; если же следующая клетка занята, то рассматривается одна из дислокационных реакций: аннигиляция, образование барьера, дислокационная стенка и др.

Пластическое деформирование осуществляется за счет сдвига одних частей кристалла относительно других при скольжении краевых дислокаций по активным системам скольжения. Условием активации k-й системы скольжения является достижение касательного напряжения в ней некоторого критического напряжения τ(ck ) :

где диада b(k)n(k) представляет ориентационный тензор k-й системы скольжения (здесь под b(k ) понимается единичный вектор в направлении соответствующего вектора Бюргерса), n(k ) – еди-

ничный вектор нормали к плоскости скольжения. Условие (1) называется законом Шмидта, устанавливающим момент начала неупругого деформирования при достижении в системе скольжения некоторого критического касательного напряжения τ(ck ) . Для опре-

деления начального (без учета деформационного упрочнения) критического напряжения используется так называемое (барьерное) напряжение Пайерлса–Набарро.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проекты 13-01- 96006 р_урал_а, 14-01-00069-а).

362

Список литературы

1.Трусов П.В., Чечулина Е.А. Прерывистая текучесть: физические механизмы, экспериментальные данные, макрофеноменологические модели // Вестник Пермского национального исследовательского политехнического университета. Механика. – 2014. – № 3. – С. 186–232.

2.Белл Дж.Ф. Экспериментальные основы механики деформируемых твердых тел. Ч. 1. Малые деформации. – М.: Наука, 1984. – 600 с.

3.Белл Дж.Ф. Экспериментальные основы механики деформируемых твердых тел. Ч. 2. Конечные деформации. – М.:

Наука, 1984. – 432 с.

4.Введение в математическое моделирование: учеб. пособие / под ред. П.В. Трусова. – М.: Логос, 2005. – 440 с.

КВАДРАТИЧНЫЙ НАГРЕВ ВЕРХНЕЙ ГРАНИЦЫ СЛОЯ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ

Е.Ю. Просвиряков1, В.В. Привалова2

(Институт машиноведения УрО РАН, Екатеринбург, Россия,

1evgen_pros@mail.ru, 2valentprival@gmail.com)

Приведено точное решение системы уравнений, описывающей конвективное течение вязкой несжимаемой жидкости на плоскости, подогреваемой точечным параболическим источником.

Ключевые слова: краевая задача, конвективное течение Куэтта, параболический нагрев, точное решение.

Уравнения Навье-Стокса, описывающие тепловую конвекцию вязкой несжимаемой жидкости, в приближении Буссинеска [2, 3] записываются следующим образом:

363

V = 0.

Вработе рассмотрено конвективное течение жидкости, описываемое системой уравнений (1) в двумерном случае (плос-

костьOxz). Ось Oz направлена по вертикали вверх. В системе уравнений (1) введены следующие обозначения: V (x, z,t ) = (Vx ,Vz ) –

вектор скорости течения; P – отклонение давления от гидростатического, отнесенное к постоянной средней плотности жидкости ρ; T – отклонение от средней температуры; ν, χ – коэффициенты кинематической вязкости и температуропроводности жидкости соответственно; γ – единичный вектор, направленный по вертикали вверх; g – ускорение свободного падения, β = –ρ–1 (∂ρ/∂T) – температурный коэффициент объемного расширения жидкости;и – дифференциальные операторы Гамильтона и Лапласа соответственно [1].

Решение системы уравнений (1) в прямоугольной декартовой системе координат определялось в виде:

T = T0 + xT1 + x2 T11 .

2

Здесь x, z – декартовы координаты. Предполагалось, что

все искомые 9 функций (U, u, w, P0, P1, P11, T0, T1, T11) зависят от координаты z и времени t. После подстановки искомых решений

364

в виде (2) в исходные уравнения (1) получили полиномиальные выражения вида:

Ak (z,t ) + Bk (z,t )x + Ck (z,t ) x22 = 0 .

После приравнивания коэффициентов к нулю в полиномиальных выражениях, получили следующую систему, состоящую из девяти уравнений в частных производных. Таким образом, система (1) будет иметь вид:

В записанной выше системе уравнений для краткости записи введены нестационарные дифференциальные операторы, описывающие диффузионные процессы:

Рассмотрен стационарный случай (все искомые функции не зависят от времени), и в системе уравнений (3) исключим все компоненты второго порядка малости. Таким образом, находилось решение следующей линеаризованной системы, описывающей в координатной форме конвективное течение Куэтта в декартовой системе координат:

365

Для нахождения постоянных интегрирования решений стационарной задачи для системы (4) сформулированы следующие граничные условия. Плоское стационарное течение слоя жидкости толщиной h между плоскостями z = 0 и z = h. На абсолютно твердой нижней границе слоя (ось Ox) для жидкости выполняется условие прилипания, а на верхней границе задана скорость течения. Пусть нижняя плоскость неподвижна, на верхней границе слоя жидкости (z = h) задан закон нагрева. Температура на нижней границе слоя равна нулю. На нижней границе выполняются условия постоянства температуры (отсчетную температуру полагаем равной нулю):

На нижней границе записываем граничные условия:

366

горизонтальный размер (масштаб). Введение этой характеристики необходимо для согласования размерностей. Также на верхней границе зададим атмосферное давление. Таким образом, граничные условия на верхней границе будут иметь вид:

Здесь A – значение скорости на верхней поверхности слоя жидкости, B – компонента завихренности, Θ – интенсивность точечного нагрева, S – заданное начальное отклонение давления от гидростатического, отнесенное к постоянной средней плотности жидкости ρ. Тогда решение системы уравнений (4), удовлетворяющей граничным условиям (5)−(7), имеет вид:

В работе было получено новое точное решение системы уравнений Обербека–Буссинеска, описывающее конвективное течение Куэттапри квадратичной нагреве свободной границе.

367

Список литературы

1.Couette M. E´tudes sur le frottement des liquides // Ann. Chim. Phys. – S´er. 6, Vol. 21. – Р. 433–510 (1890).

2.Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: в 10 т. Т. 6. Гидродинамика. – 5-еизд. – М.: Физматлит, 2006. – 736 с.

3.Современные математические модели конвекции / В.К. Андреев, Ю.А. Гапоненко, О.Н. Гончарова, В.В. Пухначев. –

М.: Физматлит, 2008. – 368 с.

ОРАСШИРЕНИИ ЦИЛИНДРИЧЕСКОЙ СКВАЖИНЫ

ВУПРУГОПЛАСТИЧЕСКОЙ СРЕДЕ, ЗАЩЕМЛЕННОЙ В ЦИЛИНДРЕ

ИСООТВЕТСТВУЮЩЕЙ МОДЕЛИ КУЛОНА–МОРА

А.А. Пургин1, Д.П. Ботанин2

(Уральский федеральный университет им. первого Президента России Б.Н. Ельцина, Екатеринбург, Россия,

1a.a.purgin@gmail.com, 2botanin-dp@uralnias.ru)

Рассматривается проблема расширении скважины в защемленной среде. Выводятся уравнения для определения напряженно-дефор- мированного состояния системы, а также уравнение для определения радиуса зоны пластичности.

Ключевые слова: поверхность текучести Кулона–Мора, расширение скважины, прессиометрия, ассоциативная текучесть, малые деформации.

Установление зависимости между передаваемым на внутреннюю поверхность скважины давление p и ее радиальным перемещением u является одной из главных задач прессиометрии. В работе [2] представлено решение в случае бесконечно-протя- женной упругопластичной среды. В данной работе представлено решение данной задачи в случае конечной упругопластичной среды, ограниченной цилиндром с радиусом R. Данное решение может быть использовано для описания поведения расширяю-

368

щейся скважины в случае, когда грунт, в котором расположена скважина, ограничен другим грунтом (скала), обладающим намного большим модулем упругости, чем первый грунт.

Распределение активного давления на внутреннею стенку скважины принято равномерно, следовательно, распределение напряжений и деформаций среды зависит только от расстояния от скважины.

Уравнение равновесия в данной плоской осесимметричной постановке может быть записано следующим образом:

В пространстве упругопластичной среды можно выделить две зоны: упругую и зону образования пластического течения, определяемую поверхностью текучести.

Уравнение поверхности текучести Кулона–Мора определяется выражением:

где с – сцепление грунта, ϕ – угол внутреннего трения.

Так как задача осесимметричная, то зона пластичности имеет круговое очертание в плане и характеризуется радиусом зоны пластичности ρ.

Частное решение уравнения (1) с учетом (2) и условием равенства радиальных напряжений на внутренней поверхности скважины активному давлению p:

369

Перемещения в пределах зоны пластичности могу быть определены с учетом ассоциативного закона текучести из следующей системы уравнений:

Постоянная интегрирования данного уравнения определяется из условия непрерывности перемещений на границе пластической и упругой зон. Перемещение на границе пластической зоны и упругой зоны может быть определено по уравнению (8).

Уравнения (3), (4), (5) действительны в области [r0 …ρ].

Поведение системы в упругой зоне описывают следующие уравнения:

370