2.1.2.Матричная форма уравнения преобразования координат точек звеньев

Матрица порядка (mn) есть система чисел (элементов), расположенных в виде прямоугольной таблицы из m строк и n столбцов:

.

Если m=n, то матрица называется квадратной порядка n.

Уравнения (2.1), (2.2) и (2.3) запишем в матричной форме. Коэффициенты правой части дают матрицу порядка (23). Удобнее использовать матрицы квадратные, поэтому к каждым двум уравнениям добавим тождество  1, получим квадратные матрицы третьего порядка.

Составим матрицу перехода из системы х₃у₃ в систему х₂у₂.

.

Запишем матрицу перехода Т₂₁.

.

Матрицу перехода Т₁₀.

.

Левые части уравнений (2.1), (2.2) и (2.3) с добавлением тождества   1 дают столбцевые матрицы третьего порядка:

.

Радиус-вектор известен, т.к. известны координаты и .

Чтобы найти значение необходимо:

; (2.4)

; (2.5)

. (2.6)

Подставим уравнения (2.4) и (2.5) в уравнение (2.6), получим

.

Это уравнение позволяет определить положение точке Е₃ в системе координат х₀у₀. Для этого необходимо перемножить матрицы T₁₀ и Т₂₁, а затем (T₁₀Т₂₁)T₃₂ и столбцевую .

.

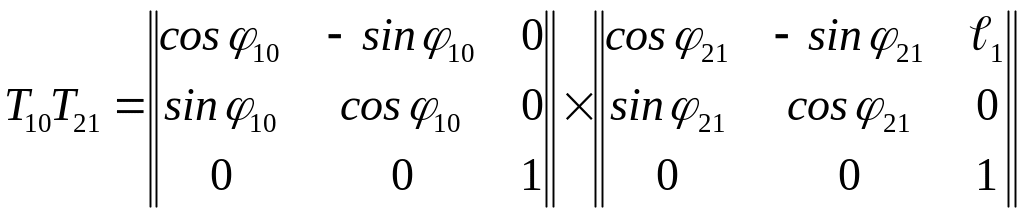. (2.7)

Матрицу (2.7) умножаем на матрицу T₃₂ и столбцевую матрицу :

.

Получим:

. (2.8)

Уравнения (2.8) можно было бы получить, решая уравнения (2.1), (2.2) и (2.3), но вычисления заняли бы больше времени. Матричная форма записи и решения уравнений удобнее. Для решения таких уравнений существуют стандартные программы, используемые на ЭВМ.

Уравнение (2.8), определяющее положение точки E₃ относительно х₀у₀, можно получить и иным способом, а именно – составить уравнение проекции контура 0₁0₂0₃E₃ в системе х₀у₀.

Однако метод проекций получается сложнее метода преобразования координат для пространственных механизмов.

2.1.3.Определение положений, скоростей и ускорений звеньев пространственных механизмов

При кинематическом анализе механизмов по заданному закону движения ведущих звеньев определяем положение, скорость и ускорение ведомых звеньев механизма. Ведомые звенья являются исполнительными в машине, поэтому знание вышеназванных параметров совершенно необходимо при эксплуатации машин и механизмов.

Токарный станок. Для чего здесь необходимо знать скорости ведомых звеньев? Скорость является одним из главных факторов выбора оптимального режима резания. От скорости резания зависит чистота обработки поверхностей. Скорость надо знать.

Знание ускорений необходимо для определения сил инерции, возникающих в механизмах. С учетом сил инерции ведется силовой и прочностной расчет механизма.

Задачу определения положений, скоростей и ускорений ведомого звена рассмотрим на примере пространственного кривошипно-ползунного механизма (рис. 2.2).

Степень свободы данного механизма равна единице, W=1, т.е. задана одна обобщенная координата, это угол поворота кривошипа АВ, ₁₀. Угол ₁₀ задается как функция времени.

Удобно перемещение звеньев механизма рассматривать относительно неподвижной системы координат. Неподвижную систему координат связываем со стойкой механизма. Ось x₀ неподвижной системы направим параллельно линии движения ползуна, ось у₀ будет направлена перпендикулярно линии движения ползуна. Причем плоскость х₀Ау₀ выбирается еще и так, чтобы кривошип АВ лежал в этой плоскости. Ось z₀ направим по оси вращения кривошипа.

Рис. 2.29

Обозначим координату точки С по оси у₀ через ₃, а по оси z₀ через ₀. Текущее значение перемещения точки С будет определяться одной переменной координатой x_0C по оси х₀.

Выберем еще две подвижные системы координат. Одну свяжем с кривошипом, вторую с шатуном. С шатуном свяжем систему x₂y₂z₂, где x₂ направим по шатуну ВС, z₂ – по оси пальца шатуна, y₂ перпендикулярно плоскости x₂Вz₂. Такой выбор системы координат позволяет определить положение точки С в системе x₂y₂z₂ одной координатой, а именно:

. (2.9)

Чтобы выразить перемещение ползуна х_0С через обобщенную координату ₁₀, подвижную систему x₁y₁z₁ свяжем с кривошипом АВ так: ось z будет параллельна оси z₀, ось y₁ окажется в ₁ плоскости x₀Аy₀, а x₁ направим по кривошипу АВ.

Углы между осями x₂ и x₁ обозначим через ₂₁, а между z₂ и z₁ – через ₂₁. Последовательным переходом из системы x₂y₂z₂ в систему x₁y₁z₁ и в систему x₀y₀z₀ решаем задачу нахождения положения ползуна в неподвижной системе координат. Опишем положение ползуна в системе x₁y₁z₁.

. (2.10)

Найденные координаты точки С в системе x₁y₁z₁ спроектируем на оси неподвижной системы x₀y₀z₀.

(2.11)

Выше отмечено, что

подставив эти значения в систему (2.11), получим:

(2.12)

Система (2.12) содержит три уравнения и три неизвестных:

x_0C, ₂₁, ₂₁.

Из второго и третьего уравнений системы (2.12) определяем углы ₂₁ и _21, подставляя их в первое уравнение, находим x_0С, т.е. координату положения ползуна.

Если механизм будет плоским, ₂₀=0, т.к. оси z₁z₂z₃ параллельны. В этом случае ползун будет двигаться в плоскости кривошипа. Система уравнений для определения положения ползуна примет вид:

. (2.13)

Два уравнения с двумя неизвестными. Из второго уравнения определяем ₂₁, подставив его в первое уравнение, определим положение ползуна в зависимости от обобщенной координаты ₁₀ и размеров звеньев механизма ₁, ₂, ₃.

Для определения скорости и ускорения перемещения ползуна необходимо систему уравнений (2.12) продифференцировать по времени.

Первое дифференцирование системы (2.12) дает возможность получить систему линейных уравнений для определения скорости перемещения ползуна.

Из третьего и второго уравнения полученной системы (2.14) находим ₂₁ и ₂₁, подставив их в первое уравнение, получим возможность определить скорость перемещения ползуна в зависимости от угла поворота ₁₀ кривошипа и угловой скорости ₁₀ кривошипа. Повторное дифференцирование уравнений системы (2.12) позволяет определить ускорение ползуна.

(2.14)