4.2.3.Направленный поиск

Большой объем вычислений, необходимых для реализации случайного поиска, требует использовать в синтезе механизмов другие методы.

При направленном поиске переход от одного вектора R параметров синтеза к другому производится так, чтобы значения целевой функции, как правило, уменьшались. В таком случае можно говорить, что параметры синтеза изменяются в направлении уменьшения значений целевой функции.

Методы направленного поиска отличаются способами выбора направления, по которому изменяются параметры синтеза. Наиболее широко используется метод циклического покоординатного спуска и метод градиентного спуска.

Циклический покоординатный спуск ведется в следующем порядке:

1. Выбирается некоторый вектор R⁽¹⁾ параметров синтеза и проверяются ограничения задачи оптимизации. Если R⁽¹⁾ не лежит в области G допустимых параметров синтеза, то выбирается каким-либо способом другой вектор R⁽¹⁾, лежащий в области G.

2. Для вектора R⁽¹⁾ вычисляется целевая функция Ф₁= Ф(R⁽¹⁾).

3. Изменяется один из компонентов вектора R (один из параметров синтеза), например r₁, на величину r₁, столь малую, чтобы компонент r₁+r₁ удовлетворял ограничениям. При прочих неизменных параметрах синтеза вычисляется значение Ф₂ целевой функции. Если оно уменьшилось в сравнении с Ф₁, то направление изменения параметра r₁ является правильным и ЭВМ запоминает новое значение целевой функции Ф₂ и параметра синтеза. Если же Ф₂ > Ф₁, то знак приращения r₁ изменяется на обратный и вычисляется значение Ф при r₁–r₁ и прочих неизменных параметрах синтеза. Новое значение Ф либо уменьшается по сравнению с Ф₁, либо увеличивается (если Ф₁ есть минимум Ф), либо остается равным Ф₁.

4. Затем по тому же принципу изменяются остальные параметры синтеза (компоненты вектора R). На этом завершается первый цикл изменений параметров синтеза.

5. Следующий цикл изменений начинается с изменения какого-либо из параметров синтеза, чаще всего r₁. Эти изменения продолжаются до тех пор, пока целевая функция не достигнет минимума или станет очень медленно изменяться.

Название этого метода основано на том, что вектору R в пространстве параметров синтеза соответствует точка с координатами, равными компонентам вектора R, то есть проекциям вектора R на соответствующие оси. При изменении одного из компонентов вектора R конец вектора R перемещается в пространстве параметров синтеза вдоль прямой, параллельной одной из координатных осей. Так, например, приращению r₁>0 в двумерном пространстве параметров синтеза соответствует движение вдоль оси r₁ из точки A(r_1, r₂) в точку В(r₁+r₁r₂) (рис. 4.5), при котором конец вектора R скользит вдоль отрезка АВ.

Рис. 4.79

Метод циклического покоординатного спуска может использоваться при широких предположениях о свойствах целевой функции. Он требует только ограниченности целевой функции в области G.

В тех случаях, когда целевая функция Ф ограничена и дифференцируема по параметрам синтеза всюду внутри и на границе области G, можно вычислить вектор

,

являющийся вектором-градиентом целевой функции, показывающим направление скорейшего возрастания целевой функции. Этот вектор при простой функции Ф получается аналитически, а при сложной функции Ф с помощью вычислений по простым формулам типа .

Если изменять параметры синтеза в направлении, противоположном направлению вектора – градиента, то целевая функция будет, как правило, убывать. Так, например, если

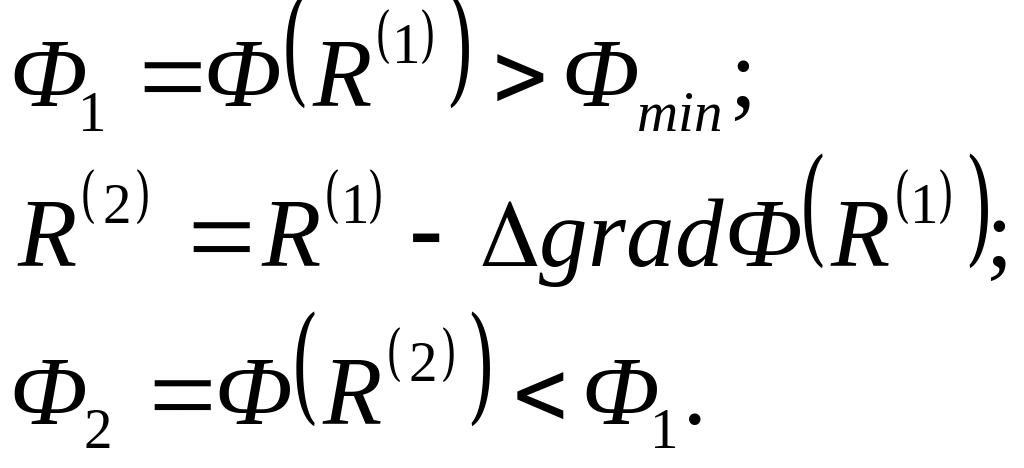
Здесь обозначение показывает, что вектор-градиент вычисляется в точке R⁽¹⁾. Величина  должна быть не очень малой, так как это замедляет процесс оптимизации, и не очень большой, так это может привести к выходу вектора R⁽²⁾ из области G.

В точке минимума целевой функции все ее частные производные по параметрам синтеза равны нулю, то есть .

В пространстве произвольного измерения поиск минимума целевой функции методом градиентного спуска производится следующим образом:

1. Задается вектор R⁽⁰⁾ и проверяются ограничения, то есть принадлежность вектора R⁽⁰⁾ области G. Если , то изменением компонентов вектора R⁽⁰⁾ каким-либо образом вводят его в область G.

2. Если , то для вектора R⁽⁰⁾ вычисляется значение целевой функции и компоненты вектора .

3. Рассматривается вектор

,

где  – шаг вычислений, выбираемый на основе опыта вычислений. Величина  не должна быть слишком большой (при этом возможен выход вектора R из области G) и не слишком малой (при этом замедляется процесс поиска минимума R).

Подбирая  = ^*, добиваются выполнения условия

.

4. По выбранному  вычисляется вектор

,

который вместе c значением Ф₁ запоминается ЭВМ.

Процесс поиска продолжается до тех пор, пока либо целевая функция перестает изменяться, что возможно при выходе на границу G, когда дальнейшее движение в антиградиентном направлении выводит вектор R из области G, либо выполняется условие

.

В двумерном пространстве параметров синтеза процесс градиентного спуска допускает наглядное изображение. На рис. 4.6 показана область G допустимых параметров синтеза, а в ней кривые, являющиеся множествами точек, для которых целевая функция сохраняет постоянное значение (линии уровня).

Как известно, вектор-градиент ортогонален поверхностям или линиям уровня. Поэтому если задана точка ,то движение из точки А, при котором целевая функция уменьшается, должно происходить вдоль прямой, ортогональной линии уровня в точке А, в направлении, обратном градиентному направлению. В результате получается новый вектор параметров синтеза

,

определяющий точку B с координатами . Далее вычисляется градиент в точке В и в направлении, обратном градиенту, производится движение из точки В в точку С и т.д. до тех пор, пока не будут выполнены условия окончания процесса поиска минимума целевой функции.

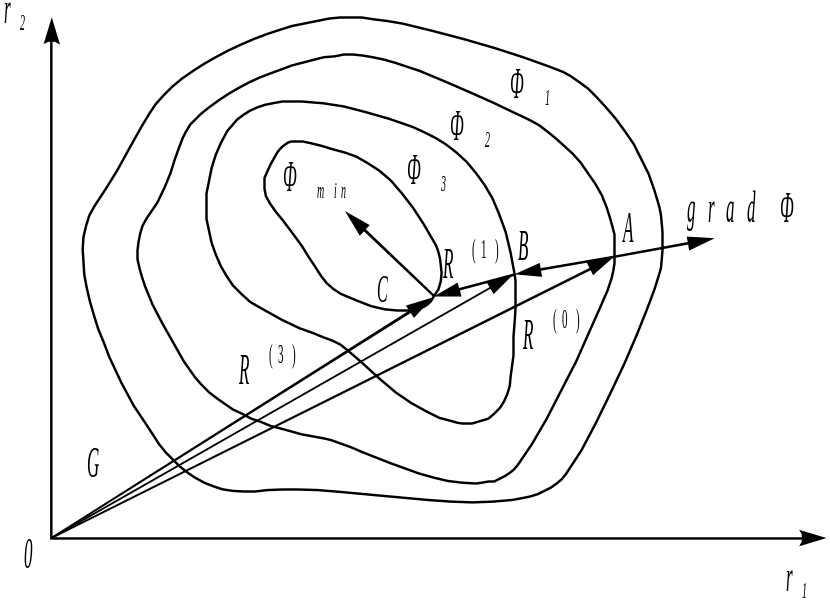
Рис. 4.80

Достоинством метода градиентного спуска является то, что он быстро приводит к области параметров синтеза, в которой значения целевой функции близки к минимуму. Однако, чем ближе к точке минимума, тем меньше значения компонент вектора. В связи с этим проекции вектора-градиента, вычисляемые по формуле

где ,

при приближении к точке минимума функция Ф стремится к нулю и сильнее начинаются сказываться погрешности вычислений. Поэтому сходимость метода градиентного спуска вблизи точки минимума целевой функции сильно замедляется. Однако, не смотря на это, метод градиентного поиска имеет большую скорость сходимости, чем метод циклического покоординатного спуска.