1.9.Структурные группы пространственных механизмов
Принцип образования механизмов является общим для плоских и пространственных. Условие существования пространственных структурных групп то же, т.е. W=0.
Степень свободы определяется выражением
W = 6n – 5Р5 – 4Р4 – 3Р3 – 2Р2 – Р1.
Пусть пространственный механизм состоит из звеньев, соединенных парами только 5-го класса (рис. 1.25). Структурная формула для него имеет вид W=6n-5Р5. Условие существования групп: Wгр. = 0, т.е. 6n=5Р5. Структурная группа будет выглядеть так: n = 5; 5Р5=6n; W=0.
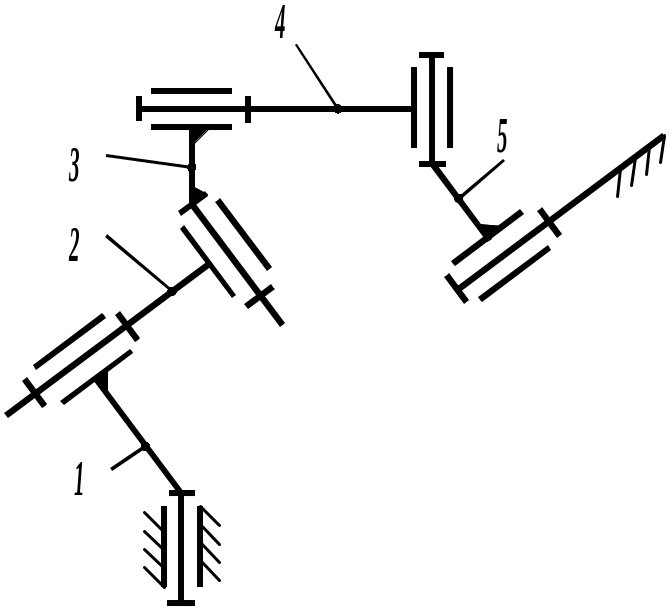
Рис. 1.25
Структурная группа получается громоздкой. Выберем другой состав звеньев и пар в механизме (рис. 1.26).
W = 6n – 5Р5 – 4Р4 – 3Р3
Условие существования группы: Wгр. = 0, т.е.
6n = 5Р5 + 4Р4 + 3Р3.
В этом случае n=2; Р5=1; Р4=1; Р3=1.
Рис. 1.26
Если такую группу присоединим к начальному звену, движение которого определяет одна обобщенная координата, получим пространственный механизм со степенью свободы равной единице (рис. 1.27)
n=3; Р5=2; Р4=1; Р3=1; W = 6 3 – 5 2 – 4 1 – 3 1 – 1.
Рис. 1.27
Следовательно, принцип образования пространственных механизмов сохраняется.
2.Анализ механизмов
2.1.Кинематический анализ механизмов
Кинематический анализ механизмов – это изучение движения звеньев механизма без учета сил, вызывающих движение. Определяющим фактором здесь является степень свободы механизма. Закон движения ведущих (начальных) звеньев известен, поэтому можно сказать, что кинематический анализ состоит в определении движения звеньев механизма по заданному движению начальных звеньев.
Основные задачи кинематического анализа следующие:
1) определение положений звеньев, включая определение траекторий движения отдельных точек;
2) определение передаточных функций, скоростей и ускорений звеньев механизма.
Методы кинематического анализа:
1) аналитические;
2) графоаналитические;
3) графические;
4) экспериментальные.
В настоящее время аналитические методы анализа выходят на первое место, чему способствует развитие ЭВМ. Однако графоаналитические и графические методы хотя и уступают в точности получаемых результатов, широко распространены из-за своей наглядности и доступности.
Ниже рассмотрено аналитическое решение задачи о положениях звеньев механизма по методу преобразования координат. Метод предложен Ю.Ф. Морошкиным.
2.1.1.Определение положений звеньев плоской незамкнутой кинематической цепи
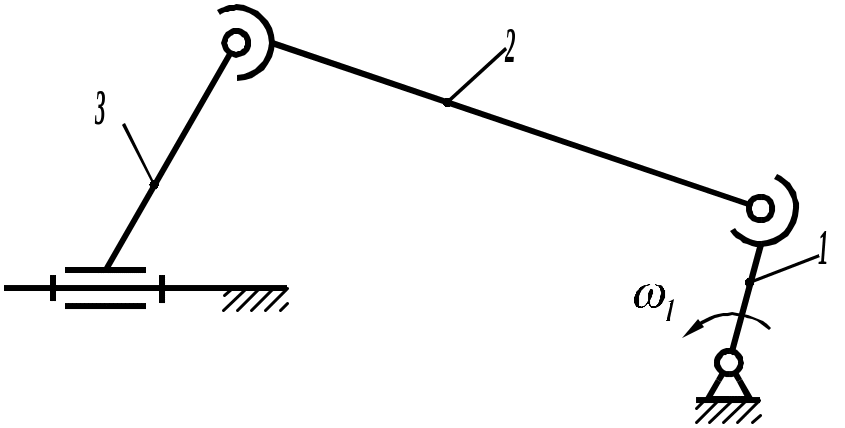
Такие кинематические цепи лежат в основе манипуляторов. Рассмотрим четырехзвенную незамкнутую цепь только с вращательными парами 5-го класса, оси кинематических пар параллельны, т.е. цепь плоская (рис. 2.1). Определим степень свободы кинематической цепи.
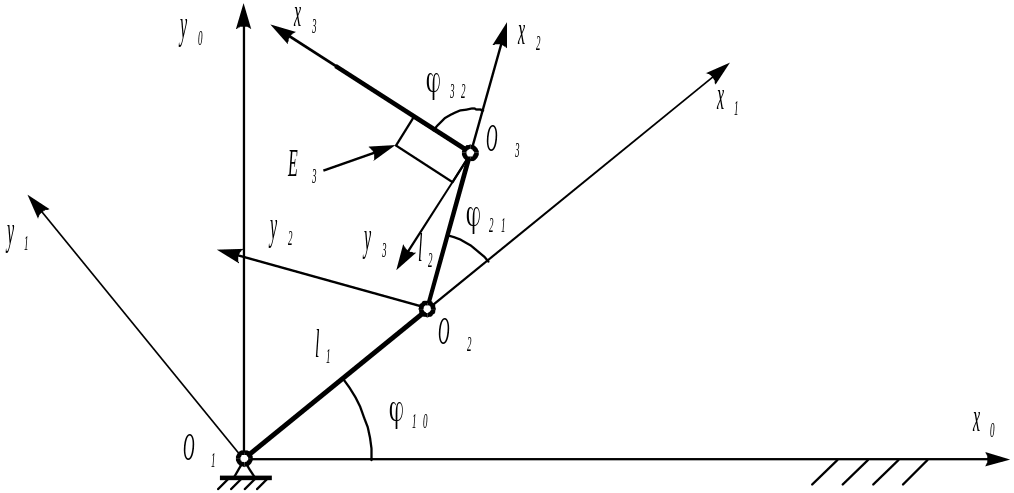
Необходимо задать три обобщенные координаты, чтобы положение звеньев относительно стойки было определено. В качестве обобщенных координат примем углы 10, 21, 32. Углы должны быть заданы как функция времени. Заданы размеры звеньев 1 и 2 и положение точки Е3 на звене 3. Положение точки Е3 задано координатами хЕ3 и yЕ3. Требуется найти траекторию точки Е3 относительно стойки.
n=3; Р5=3; W = 6 3 – 2 3 = 3.
Рис. 2.28
Со стойкой свяжем неподвижную систему координат х0, у0. Выберем системы координат х1у1, х2у2 и х3у3, связав их с положением звеньев кинематической цепи.
Положение точки Е3 звена 3 задано в системе координат х3у3 ; необходимо найти ее положение в системе х0у0 , т.е. найти координаты хЕ0 и yЕ0. Переход от системы х3у3 к системе х0у0 проведем постепенно, переходя из третьей системы во вторую, из второй в первую, из первой в нулевую.
Найдем положение точки Е3 в системе х2у2.
. (2.1)
Переходим в систему х1у1, находим координаты хЕ1 и yЕ1.
. (2.2)
Переходим в систему х0у0, находим координаты Е3 = хЕ0, yЕ0.
. (2.3)
Уравнения (2.1), (2.2) и (2.3) являются системой линейных уравнений с шестью неизвестными. Они дают возможность определить траекторию точки Е3 , т.е. определить её положение относительно системы х0у0. Метод преобразования координат более удобен, если воспользоваться матричной формой.